具有扩展结构的多倒立摆分散关联预设有限时间跟踪控制
2023-05-22周丽文李小华
周丽文,李小华,杨 伊
(辽宁科技大学 电子与信息工程学院,辽宁 鞍山 114051)
弹簧连接的多倒立摆系统常用来模拟实际非线性大系统,以检验控制策略的有效性.Siljak于1972年首次提出关联稳定性[1]概念,此后非线性大系统的关联稳定控制得到广泛研究[2-7].有限时间控制虽有较快的收敛速度和较高的鲁棒性[8-10],但不能满足系统暂态性能要求.预设性能控制可同时改善系统暂态性能和稳态性能,得到学者的关注,取得了不少研究成果[11-16].文献[17]研究了非线性大系统的预设性能控制,使用双曲正切函数处理互联项,但没有研究有限时间控制.文献[18]将预设性能控制与有限时间控制相结合,提出了预设有限时间控制,构建了一个预设有限时间性能函数,基于Backstepping技术设计了预设有限时间控制器.在文献[19]给出的双倒立摆系统动力学模型的基础上,该文建立随机激励下具有扩展结构的弹簧连接的多倒立摆系统的数学模型,设计具有扩展结构的弹簧连接的多倒立摆系统的分散关联预设有限时间跟踪控制器.
1 系统描述
1.1 随机激励下弹簧连接的双倒立摆系统的数学模型
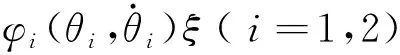
(1)
其中:Ji为转动惯量;θi为摆杆与竖直方向的夹角;mi为摆杆质量;g为重力加速度;r,b,k,l分别表示摆杆长度、相邻摆杆底部半球的球心间距、弹簧的弹性系数、弹簧的自然长度;ui为电机在摆杆底部施加的转矩.
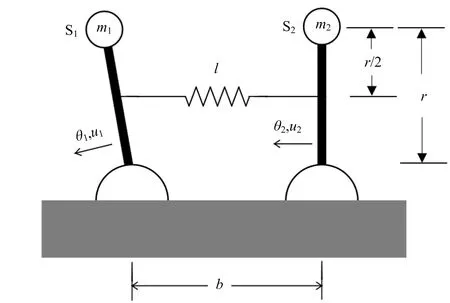
图1 随机激励下弹簧连接的双倒立摆系统
(2)
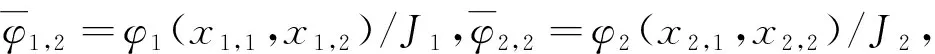
(3)
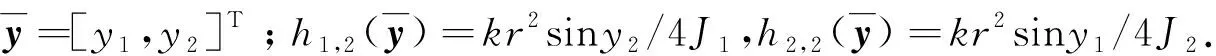
1.2 随机激励下具有扩展结构的弹簧连接的多倒立摆系统的数学模型
在图1系统结构的基础上,将倒立摆S3加入其中,得到随机激励下具有扩展结构的弹簧连接的多倒立摆系统,如图2所示.
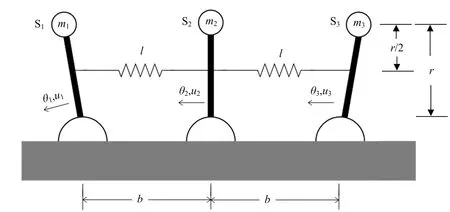
图2 随机激励下具有扩展结构的弹簧连接的多倒立摆系统
倒立摆S3的动力学方程为
(4)
(5)
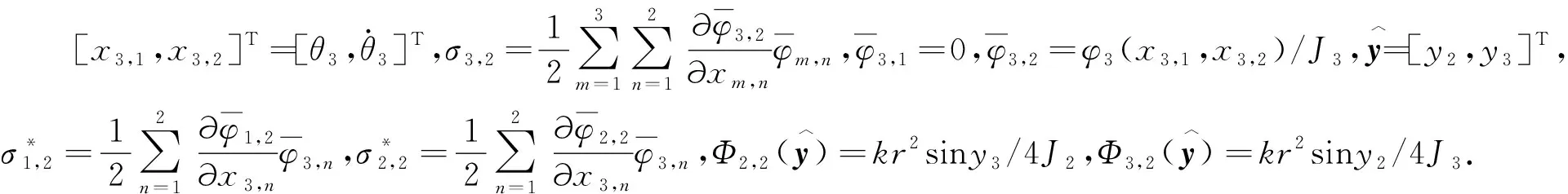
使用Backstepping方法,该文首先为系统(3)设计分散关联预设有限时间跟踪控制器,然后为结构扩展后的系统(5)设计分散关联预设有限时间跟踪控制器,确保:(1)新加入的子系统S3的输出信号y3(t)能跟踪给定的参考信号y3,d(t),且跟踪误差e3(t)能被预设有限时间性能函数Γ(t)约束;(2)新加入的闭环子系统S3及扩展后的系统(5)中的所有信号均随概率有界稳定;(3)扩展后的系统(5)是关联稳定的.
对系统做如下假设:
假设1参考信号yi,d(t) (i=1,2,3)及其1阶导数是已知函数且连续有界.

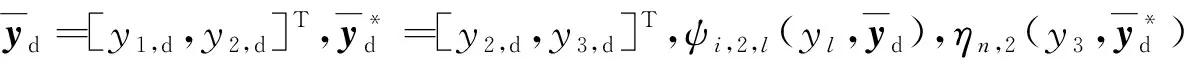
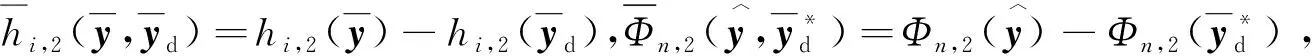
其中:el(t)=yl(t)-yl,d(t)(l=1,2),e3(t)=y3(t)-y3,d(t).
2 预备知识
考虑如下随机系统
dx=f(x)dt+h(x)dw, ∀x∈n,
(6)
其中:x∈n为系统状态向量;w表示r维布朗运动参量;f(x):n→n和h(x):n→n×r均为满足局部Lipschitz 条件的连续函数,且f(0)=h(0)=0.
定义1[20]对任意函数V(x)∈2,定义无穷微分算子L,其与V(x)作用后的式子为
其中:tr{·}为矩阵的迹.
定义2[18]光滑函数Γ(t)满足
(1)Γ(t)>0.


则Γ(t)为预设有限时间性能函数.
预设有限时间性能函数[18]为
其中:Tf>0,Γ0≥1,ΓTf>0,Γ(0)=Γ0+ΓTf.
定义3[4]对系统(5),无论子系统互联是否存在,若分散控制律向量u=[u1,u2,u3]T能使该大系统稳定,则称大系统是关联稳定的.
引理1[21]若S(Z)及S(Zl)均为RBF(radial basis function)神经网络基函数向量,其中Z=[z1,z2,…,zn]T,Zl=[z1,z2,…,zl]T均为输入向量,l和n均为正整数,且l≤n,则‖S(Z)‖2≤‖S(Zl)‖2成立.
3 控制器设计
3.1 弹簧连接的双倒立摆系统的分散关联预设有限时间跟踪控制器设计
考虑如下坐标变换
(7)
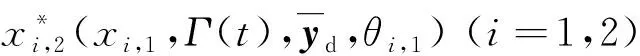
弹簧连接的双倒立摆系统的分散关联预设有限时间跟踪控制器的设计步骤如下:
第1步 选取Lyapunov 函数为
(8)
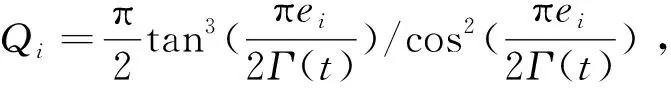
(9)
根据Young’s不等式,可得
(10)
(11)
其中
(12)
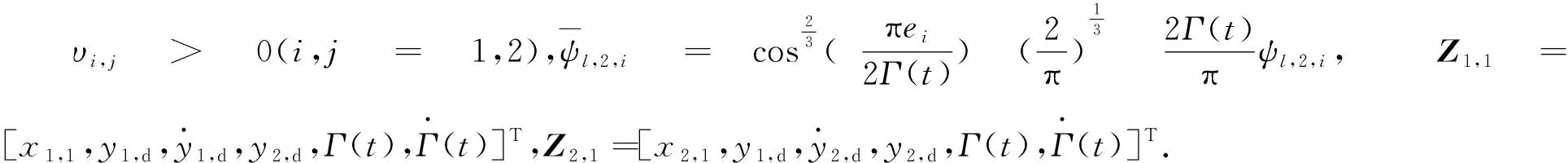
利用RBF神经网络逼近Fi,1(Zi,1),可得
(13)
根据引理1和Young’s不等式,可得
(14)
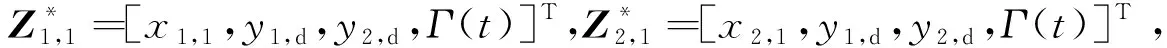
把式(14)代入式(11),可得
(15)
(16)
(17)
其中:设计参数ρi,j>0(i,j=1,2).将式(16)~(17)代入式(15),可得
(18)
第2步 选取Lyapunov函数为
(19)
由定义1,可得
(20)
根据假设2和Young’s不等式,可得
(21)
(22)
将式(21)~(22)代入式(20),并做与第1步类似的加减处理,可得
(23)
(24)
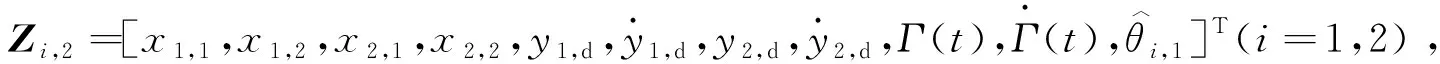
用 RBF神经网络逼近Fi,2(Zi,2),可得
(25)
根据引理1和Young’s不等式,可得
(26)

(27)
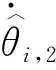
(28)
(29)
将式(28)~(29)代入式(27),可得
(30)
选取系统(3)的Lyapunov函数为
(31)
根据式(18),(30),可得
(32)
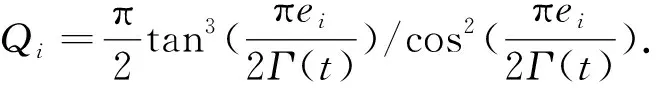
根据等式间的变换关系,可得
(33)

(34)
(35)
将式(34)~(35)代入式(32),可得
(36)
其中
a0=min{4c,ρi,j(i=1,2,j=1,2)},
(37)
(38)
3.2 具有扩展结构的弹簧连接的多倒立摆系统的分散关联预设有限时间跟踪控制器设计
当系统(3)加入新的子系统S3扩展后,新增子系统与系统(3)间出现了新的互联项,而系统(3)的虚拟控制律、实际控制律及自适应律不能使其稳定,因此需重新设计控制器.具有扩展结构的弹簧连接的多倒立摆系统的分散关联预设有限时间跟踪控制器设计的步骤如下:
第1步 选取子系统S1的Lyapunov函数为
(39)
经与3.1节的第1步类似的推导,可得
(40)
第2步 选取子系统S1的Lyapunov函数为
(41)
由定义1,可得
(42)
第3步 选取子系统S2的Lyapunov函数为
(43)
经与3.1节的第1步类似的推导,可得
(44)
第4步 选取子系统S2的Lyapunov函数为
(45)
由定义1,可得
(46)
其中
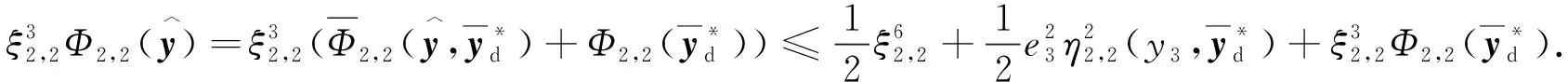
(47)
将式(47)代入式(46),可得
(48)
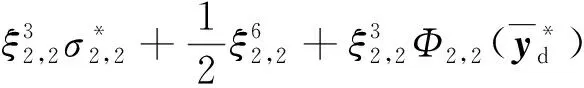
考虑如下坐标变换
(49)
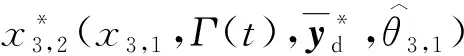
第5步 选取子系统S3的Lyapunov函数为
(50)
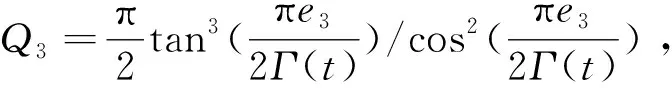
(51)
根据Young’s不等式,可得
(52)
把式(52)代入式(51),且进行加减处理,可得
(53)
(54)
(55)
根据引理1和Young’s不等式,可得
(56)
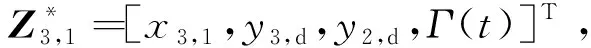
(57)
(58)
(59)
其中:设计参数ρ3,j>0 (j=1,2).将式(58)~(59)代入式(57),可得
(60)
第6步 选取子系统S3的Lyapunov函数为
(61)
由定义1可得
(62)
根据假设2和Young’s不等式,可得
(63)
(64)
将式(63)~(64)代入式(62),通过加减处理可得
(65)
其中
(66)
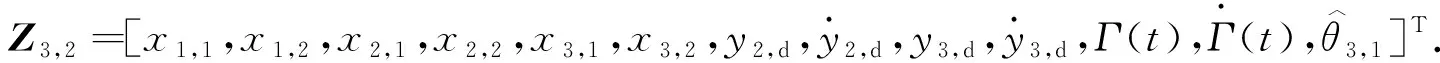
(67)
根据引理1和Young’s不等式,可得
(68)
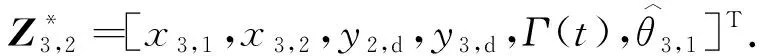
(69)

(70)
(71)
将式(70)~(71)代入式(69),可得
(72)
选取系统(5)的Lyapunov函数为
(73)
则有
(74)
与式(34)同理,可得
(75)
(76)
将式(75)~(76)代入式(74),可得
(77)
定理1因为系统(3)的控制律、自适应律分别为式(16)~(17), (28)~(29),且初始条件满足|ei(0)|<Γ(0),新加入的子系统S3的控制律、自适应律分别为式(58)~(59), (70)~(71),则对于满足假设1和2的系统(5),有
(1) 系统中的所有信号均随概率有界稳定;
(2) 系统的跟踪误差ei(t)能被预设有限时间性能函数Γ(t)约束,且在给定停息时间Tf内收敛至平衡点的一个任意给定的邻域(-ΓTf,ΓTf);
(3) 系统是关联稳定的.
证明(1) 利用式(35),(73)可将式(77)改写为
(78)
其中
(79)
(80)
因此,根据文献[20]中的引理,系统(5)中的所有信号均随概率有界稳定.
(2) 式(78)可改写为
(81)
则
(82)
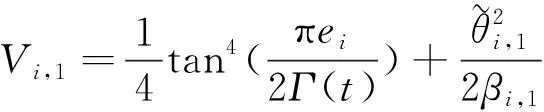
(3) 假设系统(5)的摆锤间的弹簧断开,即不存在互联,则系统(5)数学模型中的部分状态方程发生改变,其改变后的形式为
(83)
F1,1(Z1,1)变为
(84)
F1,2(Z1,2)变为
(85)
由于F1,1*(Z1,1)和F1,2*(Z1,2)均用RBF神经网络处理,且二者均有界,所以它们的神经网络逼近效果不受影响.同理,F2,1*(Z2,1),F2,2*(Z2,2),F3,1*(Z3,1),F3,2*(Z3,2)的神经网络逼近效果也不受影响.因此,LV(x)≤-a0*V(x)+b0*恒成立.根据定义3,不管系统(5)中的互联是否存在,系统(5)均能稳定,因此系统(5)是关联稳定的.至此,定理1证明完毕.
4 仿真分析
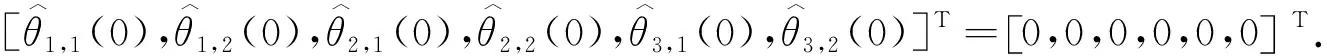
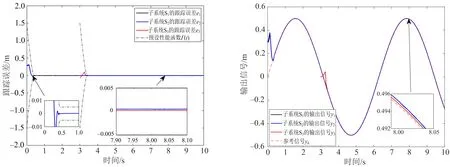
图3 子系统的跟踪误差 图4 子系统的跟踪效果
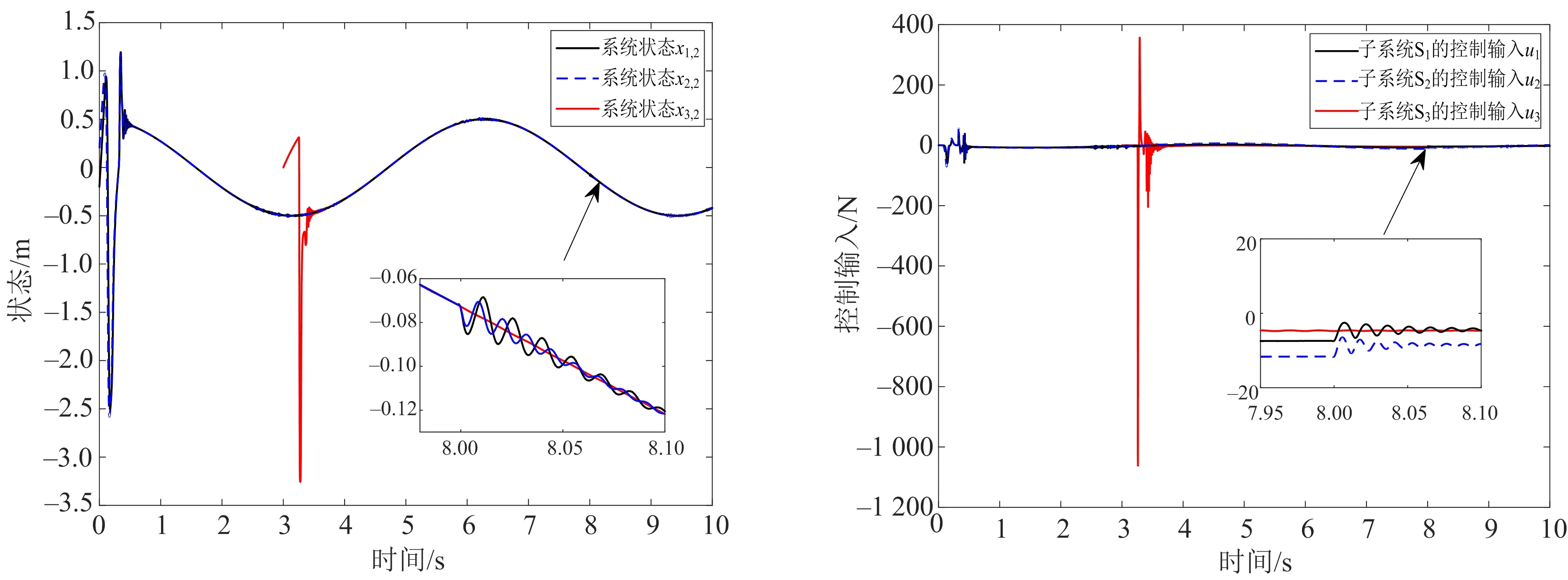
图5 系统状态变量 图6 子系统的控制输入
5 结束语
该文研究具有扩展结构的多倒立摆分散关联预设有限时间跟踪控制问题.建立了随机激励下具有扩展结构的弹簧连接的多倒立摆系统的数学模型,设计了具有扩展结构的弹簧连接的多倒立摆系统的分散关联预设有限时间跟踪控制器.在不改变原系统的控制律和自适应律的前提下,新加入子系统的控制律和自适应律使所有子系统的跟踪误差能被预设有限时间性能函数约束,系统中的所有信号均随概率有界稳定,且为关联稳定.
