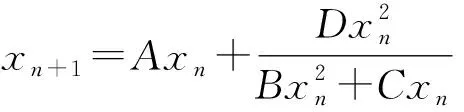一类一阶模糊差分方程解的性态分析
2023-05-22欧阳苗张千宏陈滋利
欧阳苗,张千宏,陈滋利
(1.西南交通大学 数学学院, 四川 成都 611730;2.厦门理工学院 数学与统计学院,福建 厦门 361000;3.贵州财经大学 数统学院,贵州 贵阳 550025)
近年来,随着经济学、生物学、计算机科学、智能控制等学科的飞速发展,差分方程和差分方程系统作为研究热点,被广泛运用于解决工程和生产等诸多方面的问题[1-7].实际工作环境带来的模型参数模糊不确定性、状态变量的性质初始条件的不精确性均会给系统带来一定范围内结果的波动,其解是模糊数序列.模糊集理论适用于分析不精确现象,因此对模糊差分方程动力学行为的研究也逐渐成为应用数学的研究热点[8-14].
论文利用模糊集理论,研究以下一阶模糊差分模型
(1)
的正解存在性及每个正解都有界的条件、持久性、渐近稳定性.其中:初始值x0和系数A,B,C,D均为正模糊数.
1 预备知识
定义1[15]称u:→[0,1]为模糊数,若满足条件(i)~(iv):
(i)u是正规的,即存在x∈,使得u(x)=1;
(ii)u是模糊凸的,即对于所有t∈[0,1],x1,x2∈,使得
u(tx1+(1-t)x2)≥min{u(x1),u(x2)};
(iii)u是上半连续的;

模糊数也可以用参数形式描述.
定义2[15]参数形式的模糊数u是由函数ul,ur构成的函数对(ul,ur),其中0≤α≤1 ,且满足条件(I)~(III):
(I)ul(α)有界单调递增左连续;
(II)ur(α)有界单调递减左连续;
(III)ul(α)≤ur(α),0≤α≤1.
参数形式下,实数x表示为(ul(α),ur(α))=(x,x), 0≤α≤1.{(ul(α),ur(α))}为形成一个凸锥E1的模糊数空间,它同构等距嵌入Banach空间[15].
定义3[15]任意两个模糊数u,v间的距离定义为
其中:(E1,D)是完备的距离空间.
定义4[15]令u=(ul(α),ur(α)),v=(vl(α),vr(α))∈E1,0≤α≤1且k∈,则
(1)u=v当且仅当ul(α)=vl(α),ur(α)=vr(α);
(2)u+v=(ul(α)+vl(α),ur(α)+vr(α));
(3)u-v=(ul(α)-vr(α),ur(α)-vl(α));
定义5[16]设u,v∈E1,α-截集[u]α=[ul,α,ur,α],[v]α=[vl,α,vr,α],其中0∉[v]α,∀α∈[0,1].模糊数除法运算的广义除法(g-除法)÷g对应于s=u÷gv,取α-截集[s]α=[sl,α,sr,α],定义如下
根据定义,s是正模糊数,sl,α单调不减,sr,α单调不增,sl,1≤sr,1.
注文献[16]中的模糊数为正模糊数,若u÷gv=s∈E1,则模糊数s有以下两种情形:
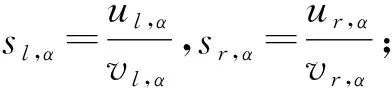
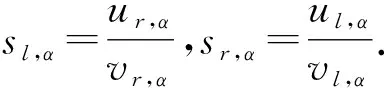
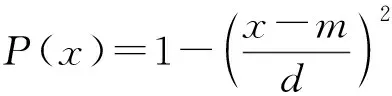
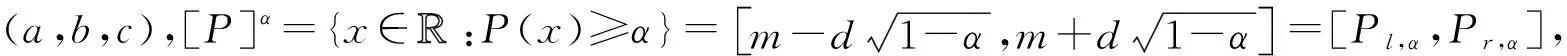
性质1[15]若{Pα:α∈[0,1]} 是紧的凸集,则n有以下非空子集族:
(b)Pα2⊂Pα1,若α1≤α2;
(c)Pα=∩k≥1Pαk,当αk↑α>0.
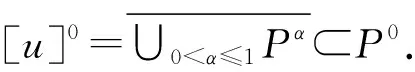
定义7[10]正模糊数序列{xn}称为持久的,如果存在正实数M,使得suppxn⊂[M,∞).正模糊数序列{xn} 称为有界的,如果存在正实数N,使得suppxn⊂(0,N],n=1,2,….正模糊数序列{xn},若范数‖xn‖(n=1,2,…)是无界数列,则称为无界.
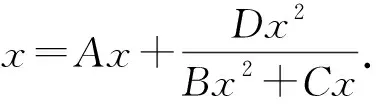
引理1[16]令f:+×××+→+为连续映射,A,B,C,D是模糊数,则
[f(A,B,C,D)]α=f([A]α,[B]α,[C]α,[D]α),α∈(0,1].
(2)
2 主要结论
2.1 方程(1)正解的存在性
定理1设模糊差分方程(1)的参数A,B,C,D和初始值x0为正模糊数,则对于任意正模糊数x0,存在初始条件为x0的唯一正解xn.
证明假设存在一个满足方程(1)初始值为x0的模糊数序列{xn},考虑它的α-截集,α∈(0,1],有
[xn]α=[ln,α,rn,α],n=0,1,2,…,
[A]α=[Al,α,Ar,α],[B]α=[Bl,α,Br,α],
[C]α=[Cl,α,Cr,α],[D]α=[Dl,α,Dr,α].
(3)
由式(1),(3)及引理1,有
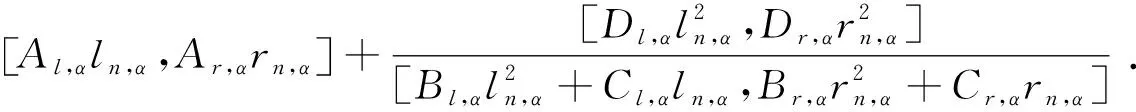
根据论文的注,{xn}的α-截集在以下两种形式中,必居其一:
(4)
(5)
在(4)式中,当n∈{0,1,2,…},α∈(0,1],有
(6)
显然对任意初始条件(l0,α,r0,α),α∈(0,1],存在唯一解(ln,α,rn,α).以下证明[ln,α,rn,α],α∈(0,1],其中(ln,α,rn,α)为系统(6)在初始值(l0,α,r0,α)下的解.确定了(1)具有初始条件x0时满足以下条件
[xn]α=[ln,α,rn,α],α∈(0,1],n=0,1,2,….
(7)
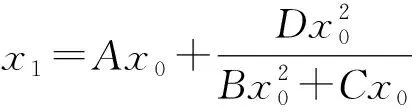
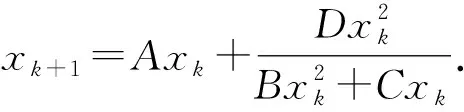
(8)
2.2 方程(1)解的性态分析
引理2对于一阶常差分方程
(9)
其中:a∈(0,1),b,c,d∈(0,+∞),y0∈(0,+∞), 有以下结论:
(i) 方程(9)的每个正解满足
(10)
(ii) 若d>(1-a)c,方程(9)有唯一正不动点
证明(i) 令{yn} 为方程(1)的正解. 当n≥0,有
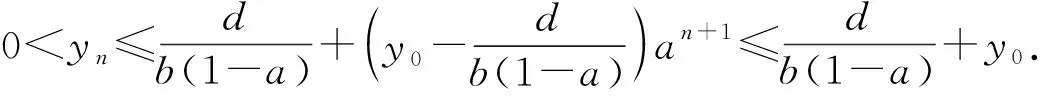
设方程(9)的不动点为y*,即yn=y*.由(9)式,有
即
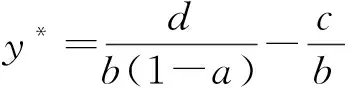
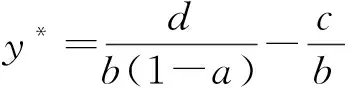
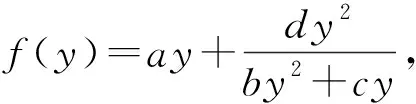
(11)
有

另一方面,由式(10)知{yn} 有界,又由式(11)知f′(y)>0,{yn}单调增加,因此
定理2一阶模糊差分方程(1),参数A,B,C,D及初值x0为正模糊数,若存在正数NA,∀α∈(0,1],Ar,α (12) 与 Dl,α>Cl,α(1-Al,α),Dr,α>Cr,α(1-Ar,α),∀α∈(0,1], (13) 则: (i) 方程(1)的解有界; (ii) 方程(1)有唯一渐近稳定的正不动点x*. 证明(i) 存在正常数MA,NA,MB,NB,MC,NC,MD,ND,M0,N0,使得 (14) 由引理2中的(i),有 (15) 由式(14),(15),有 [ln,α,rn,α]⊂[0,N],n≥1,α∈(0,1], (16) (ii) 在条件(12)下,在方程(1)两边取α-截集,得到以下带参数的差分方程系统 (17) 可得 (18) 的正解为 令xn为方程(1)满足[xn]α=[ln,α,rn,α],α∈(0,1],n=0,1,2,…的正解,则由式(17)及性质1,有 (19) 由式(16),(19)得到:对0<α1<α2<1, 有 0 (20) 因Al,α,Ar,α,Bl,α,Br,α,Cl,α,Cr,α,Dl,α,Dr,α都左连续,式(18)定义的lα,rα也左连续. 由式(14),(18),有 (21) (22) 由定义2,式(18),(20),(22),lα,rα,α∈(0,1],存在满足下式的模糊数x* (23) 由式(19),有 即方程(1)的每个正解xn,当n→∞时收敛到唯一的不动点x*.由性质2知x*全局渐近稳定. 由(5)式,有 其中:α∈(0,1],n=0,1,2,…. 引理3考虑差分系统 (24) 其中:ai∈(0,1),bi,ci,di∈(0,+∞)(i=1,2),y0,z0∈(0,+∞).若满足条件a1+a2<1 与d1d2>c1c2(1-a1)(1-a2),则: (i) 系统(24)的所有正解(yn,zn) 有界 (25) (ii) 系统(24)有唯一正不动点 (26) 证明设系统(24)的正解为(yn,zn),当n≥0, 有 所以有 得证此正解有界. 令(yn,zn)=(y,z) 为系统(24)的不动点,即 易证存在正不动点(y,z) 如式(26)所示. 定理3模糊差分方程(1)中A,B,C,D均为正模糊数,若存在正数NA,∀α∈(0,1],Ar,α (27) 则: (i) 方程(1)的正解有界; (ii) 方程(1)有唯一的正不动点x,[x]α=[lα,rα],且 其中 证明(i) 令xn是方程(1)的解,在(ii)中使用引理3,可得 (ii) 令xn=x是方程(1)的一个不动点,则 (28) 在式(28)两边取α-截集,又因为不等式(27),得到以下系统 从而得到 于是,由lα,rα组建了正模糊数x,其中[x]α=[lα,rα],α∈(0,1]. 例考虑一阶模糊差分方程 (29) 参数A,B,C,D及初始值x0均为抛物对称模糊数,比现有三角模糊数更具仿真意义. 相应地,可得 有 从方程(29)得到一组含有参数α的差分系统 显然Ar,α<1,∀α∈(0,1] 且满足式(12),(13), 抛物对称模糊解x1,x2,…,x10,如图1所示. 图1 模糊差分方程的抛物对称模糊解及对应α-截集 图2 对应α=0,0.25,0.5,0.75,1时,方程(29)在长时间下解的性态 若Dl,α≥Cl,α(1-Al,α),Dr,α≥Cr,α(1-Ar,α),α∈(0,1],方程(1)正解有界且有唯一的局部渐近稳定的正平衡点. 若Al,α+Ar,α<1且Dl,αDr,α>Cl,αCr,α(1-Al,α)(1-Ar,α),α∈(0,1], 方程(1)正解有界且有唯一的全局渐近稳定正平衡点.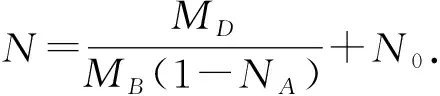
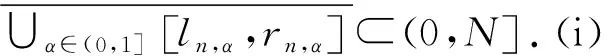

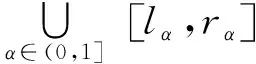
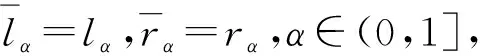
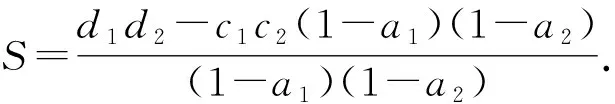
3 数值模拟
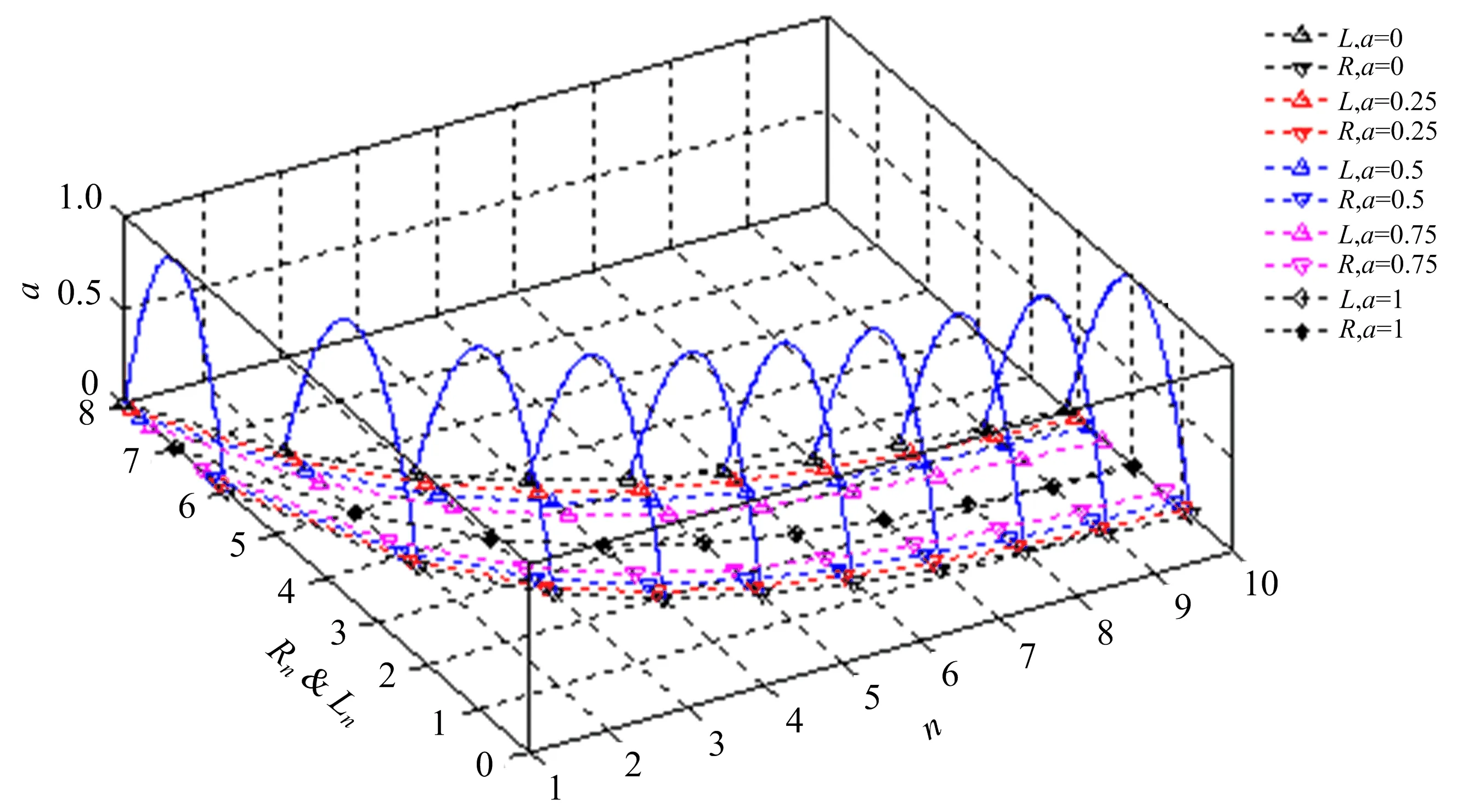

4 结束语