HULZNs环境下基于语义偏好参数的多准则群决策模型
2023-05-22毛军军朱蒙蒙李燕飞
徐 威,毛军军,2*,朱蒙蒙,李燕飞
(1.安徽大学 大数据与统计学院,安徽 合肥 230601;2.安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230601)
为了充分描述不确定信息,文献[1]中引入语言术语集并首先提出模糊集的概念.过去的几十年里,许多学者对模糊集进行了扩展研究[2-4].然而评价语言本身具有不确定性,为了表示相关信息的可靠性,Zadeh[5]提出Z-numbers概念,Z-numbers由模糊限制性和可靠性组成,能更好地反映出现实环境中的不确定性.Aliev等[6-7]讨论了Z-numbers的相关运算.
在模糊集理论的基础上,文献[8]提出不确定语言变量的概念,减少了决策过程中信息的丢失.对于语言变量的处理,主要分为两类:一种是将其对应到模糊集上进行处理,另一种是利用语言尺度函数转化为特定的值[9]再处理.基于Z-numbers和语言变量的基础,文献[10-12]提出语言型Z-numbers的相关概念.
多准则群决策问题(multi-criteria group decision-making,简称MCDM),指由决策者按各自的偏好对备选方案进行评价,寻求满意的目标或目标的排序.在前人的工作中,研究者已提出多种多准则决策方法[13-16].文献[17-18]在确定准则权重上做出了较大创新,文献[19-20]定义的不同算子拓展了多准则决策理论.
在处理语言环境下的多准则决策问题时,大多数学者忽略了决策者语义偏好不同造成的偏差.另外,在处理不确定语言变量时,区间的左右端点值虽然可以反映出专家的评价,但会造成信息的缺失.论文定义了一个含有语义偏好参数的语言尺度函数,对不确定语言变量进行离散化处理;定义了犹豫不确定语言Z-numbers(hesitant uncertain linguisticZ-numbers,简称HULZNs)的部分运算,给出信息融合方法;建立模型,并通过实例验证了论文方法的有效性.
1 预备知识
定义1[1]设S={si|i=-t,-t+1,…,0,1,2,…,t}是一个有序的语言型术语的集合,t是一个正整数,si代表语言型变量的一个可能值.称S为一语言术语集,若其中两个语言型变量满足以下两个性质:
(1) 若si≤sj,则i≤j;
(2) 服从否定运算,当i+j=0时,有neg(si)=sj.
定义2[9]设S是一个语言术语集,S={si|i=-t,-t+1,…,0,1,2,…,t}.定义语言尺度函数f:si→[0,1],f越大则表明si越优,语言尺度函数是随着下标i单调递增的函数.
定义3[5]Z-numbers是一对有序的模糊数,表示为Z=[A,B].它与一个不确定变量X相关联,其中第一个分量A是变量X的实值函数,是在值上对其的约束,第二个分量B是对第一个分量可靠性的度量.通常,A和B是用语言描述的,如(较差、不太可能)和(好、可能).
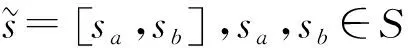
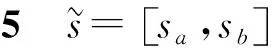
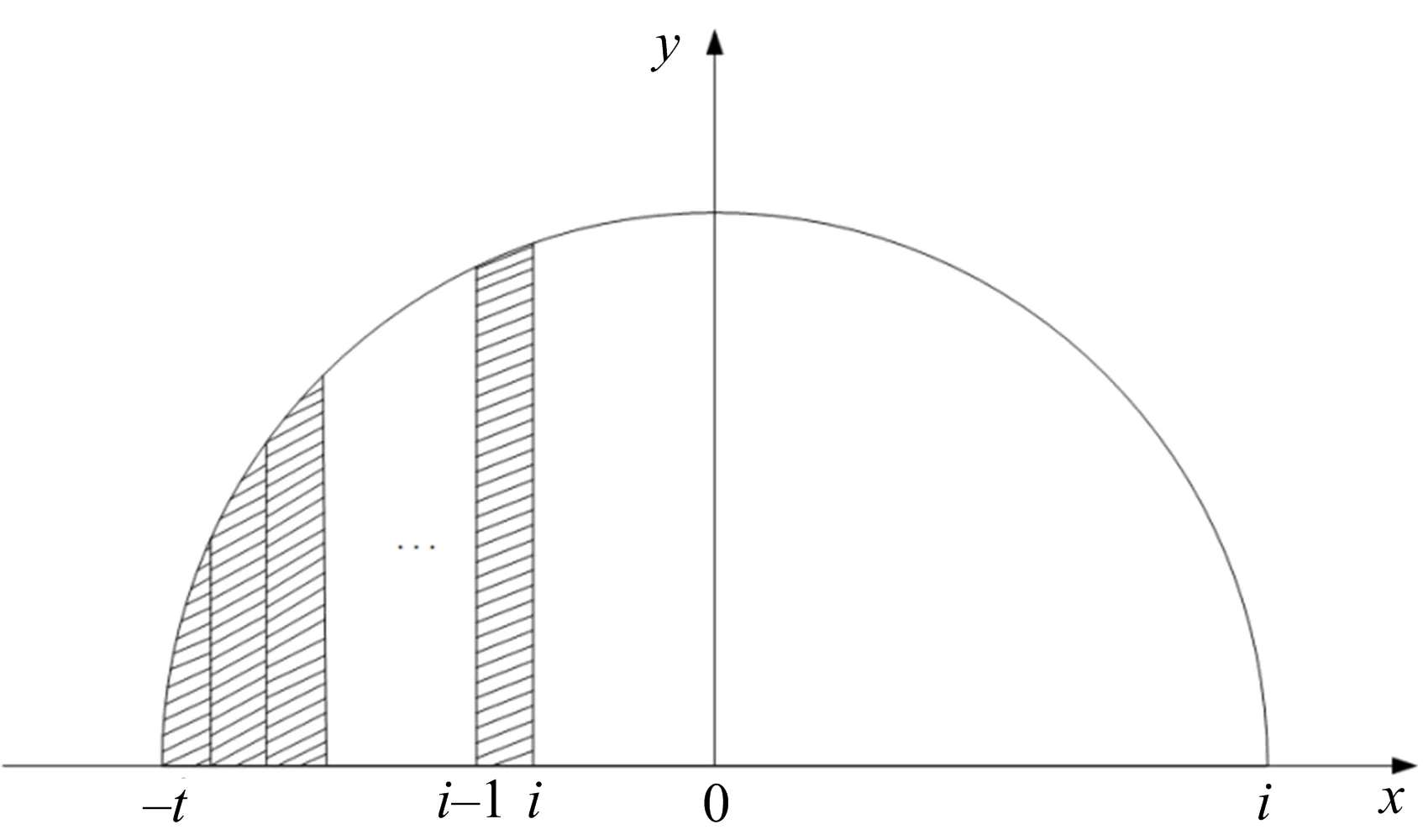
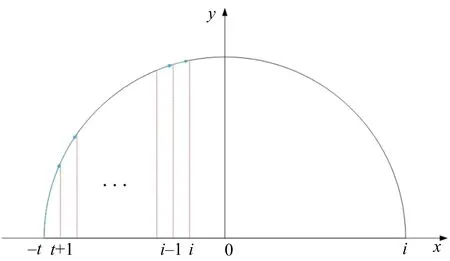
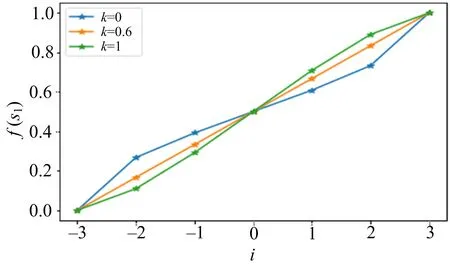
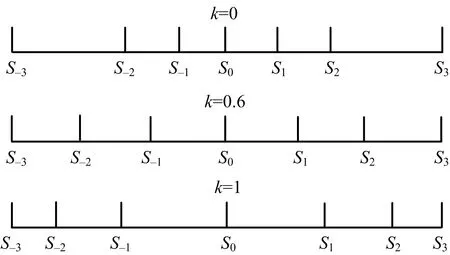
定义6[11]设X是一个论域,S={s-t,s-t+1,…s0,…,st},S′={s′-n,s′-n+1,…,s′0,…,s′n}是两个有序的包含有限个元素的语言术语的集合,代表两个不同的语义环境,t,n∈,s-t 由于客观事物的复杂性和不确定性以及人类思维的模糊性,语言变量被广泛应用于人类生活的各个方面,语义偏好分布平衡的语言尺度函数很难反映决策者的偏好次序.该节将介绍一种新型的具有良好性质的语言尺度函数,可以通过调节语义偏好参数来实现相邻语义偏差增大和偏差减小两种不平衡语言的转化. 定义7基于语义偏好分布不平衡的语言尺度函数. 设si∈S是一个语言术语集,S={si|i=-t,-t+1,…,0,1,2,…,t}.定义语义偏好分布不平衡的语言尺度函数(unbalanced linguistic scale functions,简称ULSF)f(*)如下 (1) 其反映了不同决策者对语言的理解和偏好,且满足性质1~5(性质1~3证明显而易见,论文只证明性质4,5). 性质1语言尺度函数f(si)是随着下标i单调递增的. 性质2f(si)∈[0,1],有f(s-t)=0,f(s0)=0.5,f(st)=1. 性质3如果i+j=0,那么f(si)+f(sj)=1. 有 证明 有 以k=3为例,图3,4描述了不同k下的ULSF和语义分布.图4中:当k取0的时候,反映了决策者对中间的语言术语更加敏感;如果决策者对两边的语言术语敏感,可将k取为接近1的值.例如,在投资股票时,若决策者为风险爱好者,则将k取为0,此时随着收益或亏损越大,语言尺度值变化越快;反之若决策者为保守型,在进行决策时就需要将k取为1,从而进行更准确的决策. 图1 k=1时,ULSF的几何意义 图2 k=0时,ULSF的几何意义 图3 不同k下的ULSF 图4 不同k反映了相邻语义之间的不同偏差 其中:f*,g*为语言尺度函数. Zi的得分函数与精确函数分别定义为 其中:f*为语言尺度函数,τ(Az(x))表示Az(x)离散化后的语言变量集,#Az(x)代表离散化后语言变量的个数,#Bz(x)代表Bz(x)中犹豫评价变量的个数. 设Zi,Zj为任意两个HULZNs,则: (1) 如果E(Zi)>E(Zj),则Zi>Zj; (2) 如果E(Zi)=E(Zj),则①A(Zi)>A(Zj),Zi>Zj;②A(Zi)=A(Zj),Zi=Zj. 其中:f,g为不同的语言尺度函数;lφB1,lφB2分别φB1和φB2中元素的个数. (2) HULZNPWA(Z1,Z2)=([AL,AU],∪b1∈φB1,b2∈φB2{g-1(min(maxg(φB1),maxg(φB2)))}). 其中 第一步 收集评价并将k个专家的评价标准化.在处理决策问题中,会遇到效益型和成本型等不同的准则,为了消除不同量纲对决策结果的影响,有必要将所有评估矩阵规范化.将标准化后的评价矩阵记为 效益型准则为 成本型准则为 其中:neg为3.1节中语言术语的否定运算. 第二步 利用优先加权平均算子进行信息融合.在根据得分函数和精确函数确定HULZNs的优先顺序后,将不同专家在同一准则下就方案的评价按照3.3节定义的算子进行融合,得到一个综合评价矩阵 第三步 计算准则的权重向量.准则的权重是决策问题中的重要参数,它直接影响最终结果的准确性.权重信息通常是不确定的,但是对于权重的信息会有一个粗略的范围.论文考虑最大偏差模型求权重. 有 其中:d(rij,rlj)表示综合评价矩阵中rij和rlj之间的距离,已知的部分权重信息用w∈W表示. 第四步 计算每个方案的总优势函数. P(Zi,Zj)=D(Zi,Zj)*P(zi≥zj), 其中 基于此优势函数,在根据最大偏差法确定准则权重后,定义每个方案xi的总优势函数为 显然,方案的总优势函数越大,代表相对于其他方案此方案越占优.根据总优势函数的大小,可以确定各方案之间的优先关系. 第五步 根据第四步中得到的总优势函数,对方案进行排序. 该节描述了一个实际企业的决策案例,以证明所提出方法的适用性.为了提高企业竞争力,选择合适的战略伙伴,公司成立了一个由3个专家E1,E2,E3组成的团队来协助决策.决策团队选择以下4个标准来进行判断方案是否可行以及做出最后的决策:①c1代表技术和功能;②c2代表供应商的能力和声誉;③c3代表战略的适应性:④c4代表灵活性.在经过初步的筛选和考察后,现有方案x1,x2,x3,x4可供选择.并且对于4个标准的权重信息给定以下范围 W=(0.2≤w1≤0.3,0.16≤w2≤0.35,0.12≤w3≤0.25, 0.1≤w4≤0.25,1.5w3≤w1,1.5w4≤w2). 专家的评价以HULZNs的形式给出在表1中.S={极其差,很差,差,较差,一般,较好,好,很好,极其好},S′={极其不确定,很不确定,不确定,有点不确定,中立,有点确定,确定,很确定,极其确定},收集专家的评价得到决策矩阵.为了探究语义偏好对决策结果的影响,以及语言尺度函数的性质,在进行信息融合时,分别将式(2)中f和g的参数取为0,0.6,1在一起进行比较,论文中展示的数据为k1=k2=0. 表1 专家的评估矩阵 第一步 将专家E1,E2,E3的评估矩阵进行标准化,得到标准化后的矩阵 表2 融合后的评价矩阵 第三步 根据第四节提出的数学模型计算准则权重如下 maxF(w)=0.137 6w1+0.191 1w2+0.161 3w3+0.116 4w4, 使得 用软件解得准则的权重向量为w=(0.3,0.35,0.2,0.15). 第四步 计算每个方案的总优势函数,得到Φ(x1)=0.032 2,Φ(x2)=0.091 6,Φ(x3)=0.052 0,Φ(x4)=0.039 8. 第五步 根据总优势函数对方案排序可得到x2≻x3≻x4≻x1,故最优方案为x2. 为了验证所提出方法的有效性,论文将上述方法与已有同类方法进行了对比分析.Peng[11]首先提出HULZNs的相关概念并对其定义了相关运算,随后定义出两种不同的集成算子并构造了一种新型多准则群决策模型,最终得到的结果为x2≻x1≻x4≻x3.与论文结果产生略微差距可能有以下几个原因:①在定义相关运算时,文献[11]仅考虑将区间端点进行简单相加,虽然可以大体反映出评价信息,但转化过程中会有很大的缺失,论文在信息融合过程中,将信息进行离散化处理,会大幅度地减少信息的流失;②所选取语言尺度函数不同,在对语言变量转化时会产生差异,但通过调节本文语义偏好参数可以很好地适应各种语义偏差下的决策;③在最后的方案排序中,文献[11]运用正负理想方案,论文将优势函数定义为可能度与距离的乘积更加符合现实中的决策情况. 语义偏好参数k取不同值的时候,相邻语义之间的偏差也会随之增大或减小,可以看到:当k取值在0到0.6之间的时候,语义在中间的分布较为稠密,决策人比较在意x2中等的评价;相反地,当k取值在0.6到1之间的时候,语义在两端分布较为稠密,此时反映出决策人对两边语义的敏感.为了探究参数的改变会给最后的决策结果带来何种影响,表3给出了f与g中k取不同值的决策结果(f,g中参数分别取k1,k2). 观察表3,可得到不同参数的组合,得到的结果只有两种:x2≻x3≻x4≻x1,x2≻x4≻x3≻x1.由于受到距离测度和融合方法的影响,与参考文献[11]中(1≤λ≤5时,k1=0.6,k2=1)x1,x3,x4的排序产生略微不同,但方案始终为最优方案;当λ≥5时,论文得到的第二种结果x2≻x4≻x3≻x1,与参考文献[11]得到的结果趋于一致.无论参数如何变化,方案x2始终排在第一,反映了论文所提出模型的有效性以及语义偏好参数的稳定性. 表3 由不同语义参数得到的决策结果 作为一种有效的工具,近年来,语言变量在各领域得到了广泛的应用,但在不同决策环境下相邻语言变量之间的偏差较难确定.对此,论文给出了一种含有语义偏好参数的语言尺度函数和相关性质的证明.随后结合前人的研究,定义了一种信息融合方法并建立了一个新的决策模型.该模型将语言变量进行离散化,充分利用了现实语言评价因素的不确定性,并用含有语义偏好参数的语言尺度函数减小了因为相邻语义偏差不同对决策结果造成的影响.在进行决策对方案进行排序时,将优先函数定义为可能度与距离的乘积也更加符合现实.多个专家的评价进行融合难免会造成信息量的缺失,故信息融合方法还需要进一步地优化和更深入地研究.此外,所选实例中方案过少,下一步也会将函数用到数据较多的实例中来进一步探讨语义偏好参数变化对决策结果造成的影响.2 基于语义偏好分布不平衡的语言尺度函数
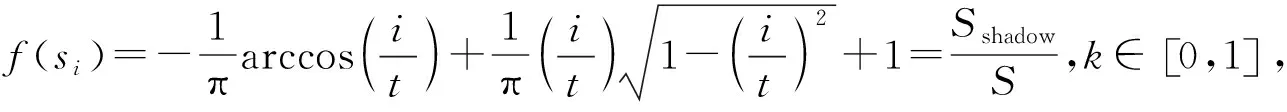

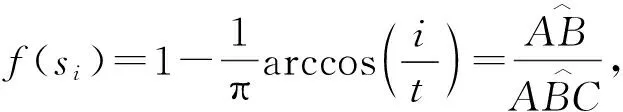
3 HULZNs之间的运算及距离公式
3.1 HULZNs之间的运算

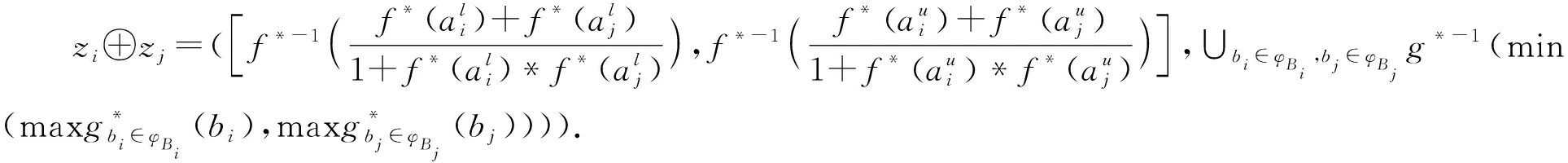
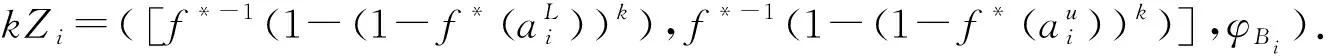
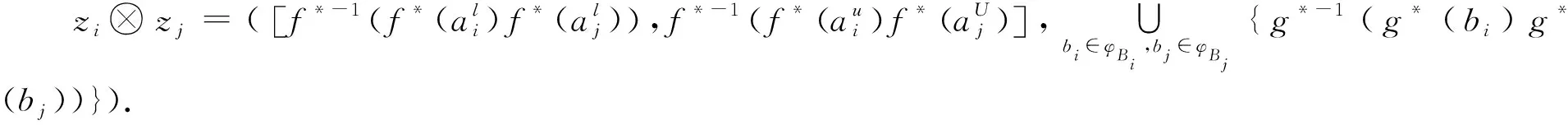

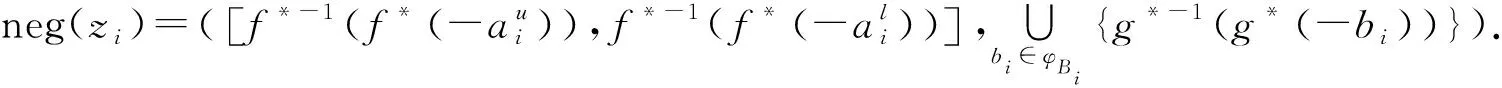
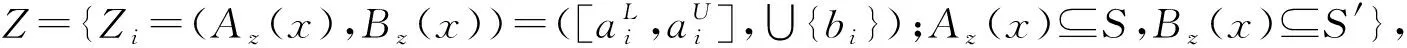
3.2 HULZNs之间的距离
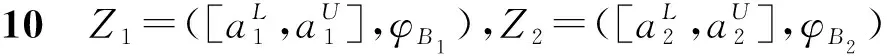
3.3 HULZNs的优先加权平均算子
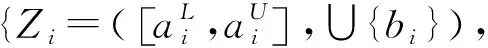
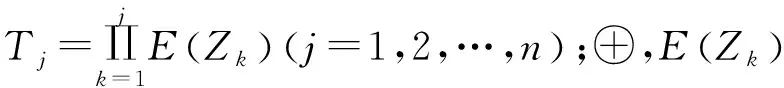
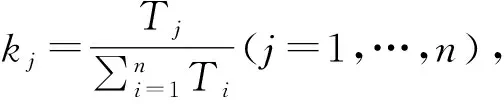
4 HULZNs环境下的多准则群决策模型
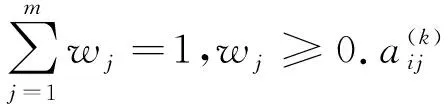
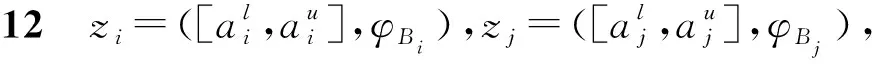
5 实例分析
5.1 模型应用
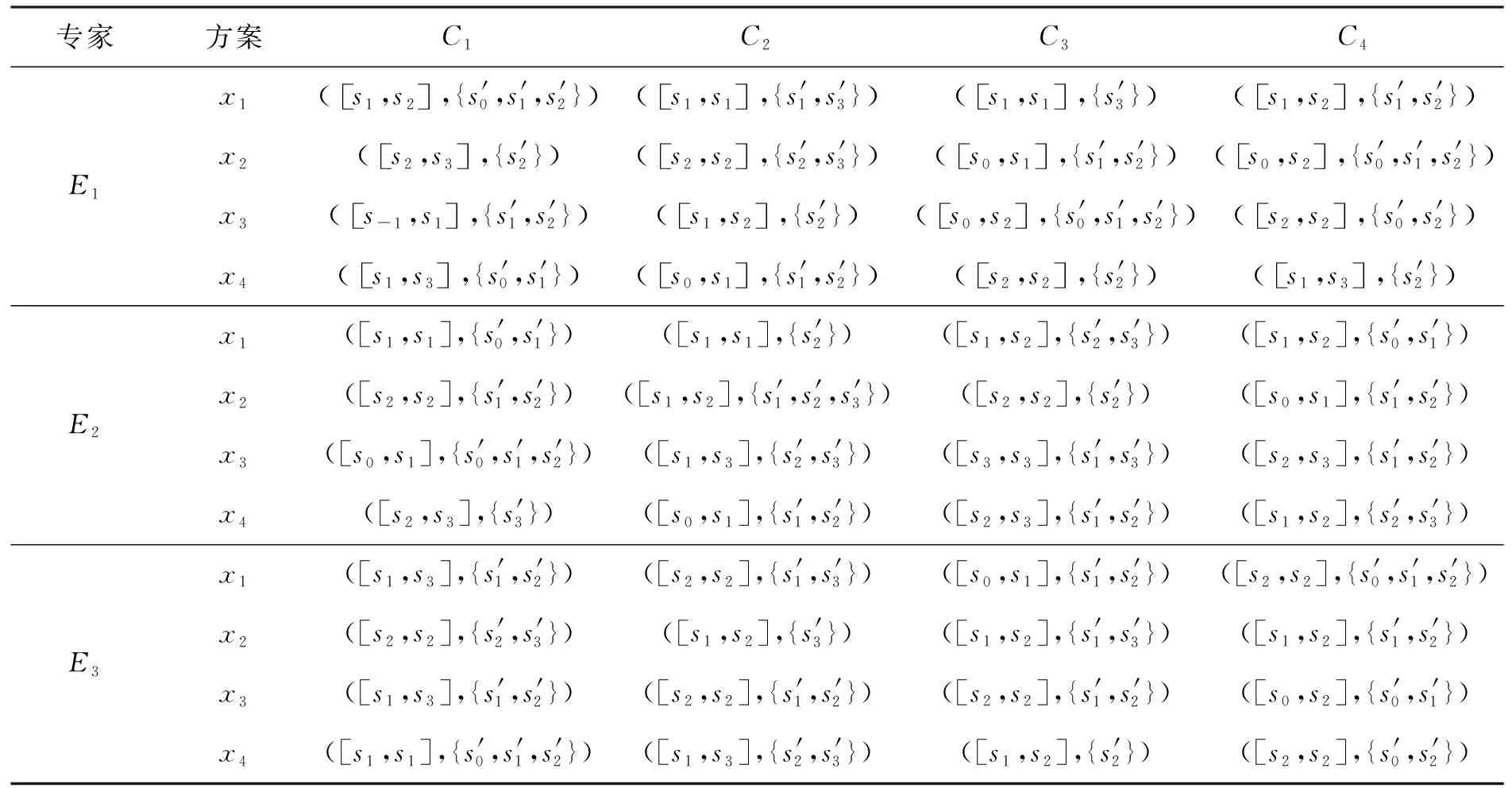
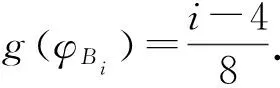

5.2 对比分析与讨论
5.3 语义偏好参数k的灵敏度分析

6 结束语
