正弦余弦算法求解含有异常值的非线性数据拟合

雍龙泉,贾 伟,黎延海

(1.陕西理工大学 数学与计算机科学学院, 陕西 汉中 723001;2.陕西省工业自动化重点实验室, 陕西 汉中 723001)

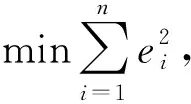
最小二乘和最小一乘都是在各自的目标函数达到最小的情形下估计参数,思想上是一致的,但由于目标函数的数学结构不同,进而造成了估计结果的差异.这种差异从统计学角度而言就形成了最小二乘和最小一乘的本质区别:最小二乘的估计结果是条件均值,最小一乘的估计结果却是条件中位数.一般情况下,如果数据的分布是对称且无异常值,则最小二乘得到的结果与最小一乘得到的结果相差不大;且使用最小二乘得到的结果具有唯一性,使用最小一乘得到的结果可能不唯一[1-5].

最小二乘法的优点在于其有良好的数学性质,可以利用非线性规划的方法求出最优解[6-7],但在计算最小一乘时,需求解一个不可微优化问题(不能很好地利用已有的非线性规划方法来计算最优解),所以很长一段时间,对最小一乘法的研究处于停滞状.1955年Charnes等通过把线性最小一乘转化为线性规划问题来求解,之后求解最小一乘的算法就不断涌现[8-15].针对非线性最小一乘如何求解还需要深入研究.

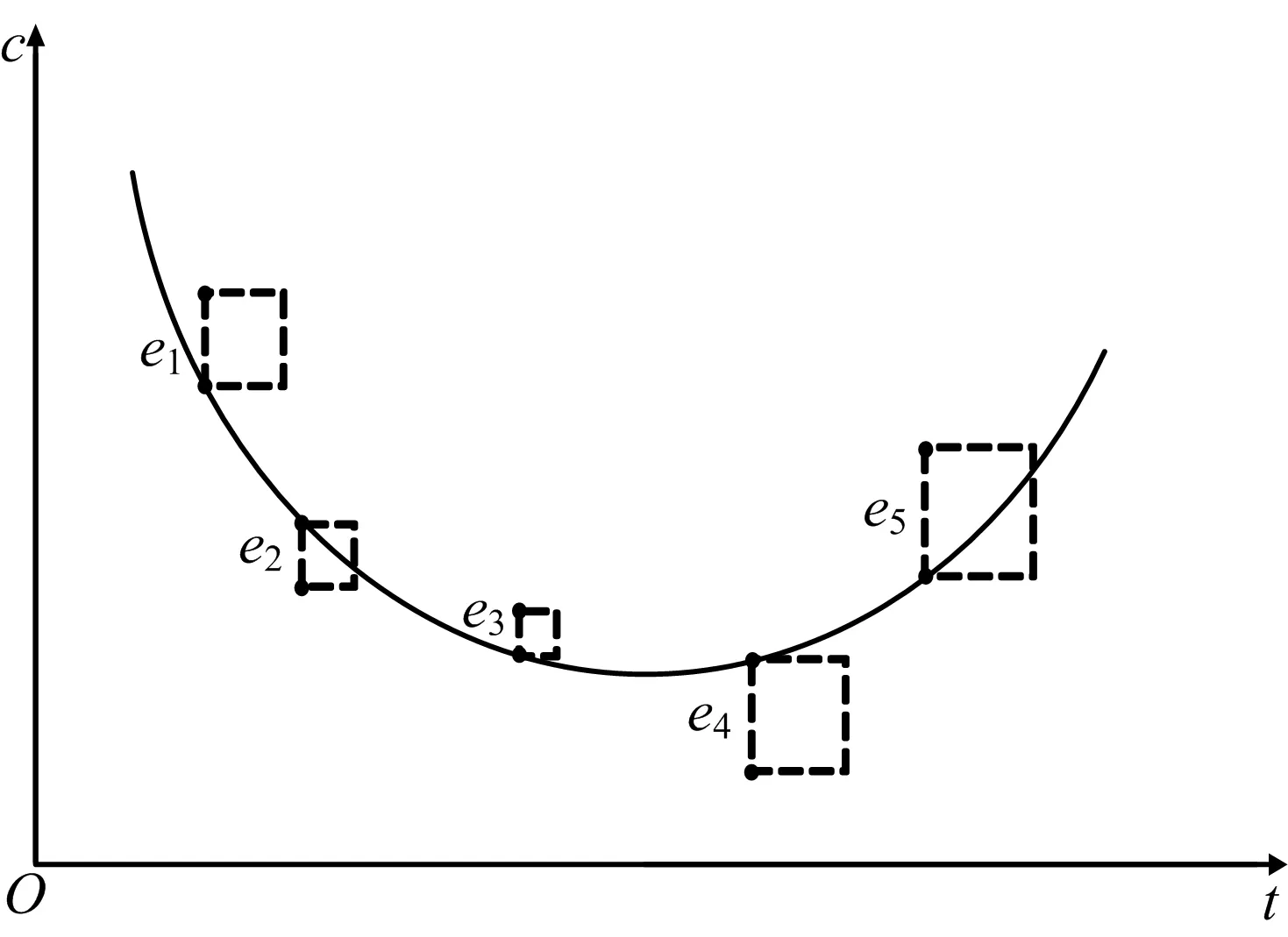
图1 非线性最小二乘拟合的几何意义

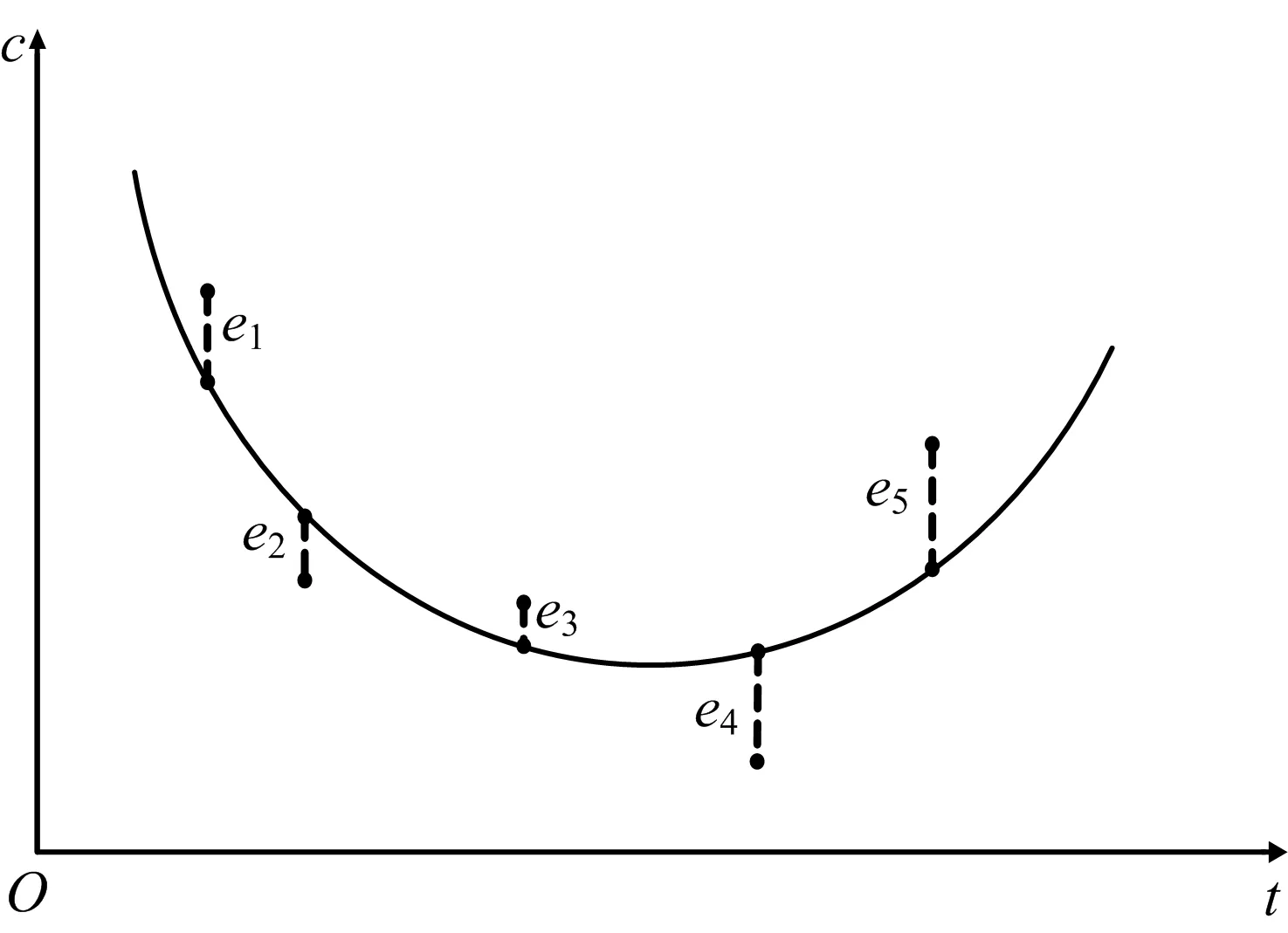
图2 非线性最小一乘拟合的几何意义

论文对给定的非线性数据分别建立了以残差为目标的非线性最小二乘与最小一乘模型,采用正弦余弦算法确定相关参数,应用于无异常值的模型和包含一个异常值的模型.结果表明最小二乘估计容易受异常值的影响,而最小一乘是残差的绝对值和而并非平方和,受异常值的影响小得多,具有比最小二乘更好的稳定性.

1 非线性拟合的数学模型

给定n组离散数据(ti,ci),i=1,2,…,n,寻找拟合曲线f(t,X),使得拟合的残差最小.论文分别建立如下优化模型

(1)

(2)

模型(1)采用最小二乘,模型(2)采用最小一乘.

2 算 法

采用一种新的启发式算法:正弦余弦算法(sine cosine algorithm, 简称SCA)来确定参数X,模型(1)与(2)是一个无约束优化问题minS(X).采用最小二乘时,目标函数为

(3)

采用最小一乘时,目标函数为

(4)

下面采用正弦余弦算法求解(3),(4).正弦余弦算法的主要步骤如下:

初始化算法参数: 种群规模N,空间维数D,控制参数a,最大迭代次数Tmax;

在可行域空间中随机初始化N个个体组成初始种群;t=1;

计算当前每个个体的适应值,并记录最优个体位置P(t);

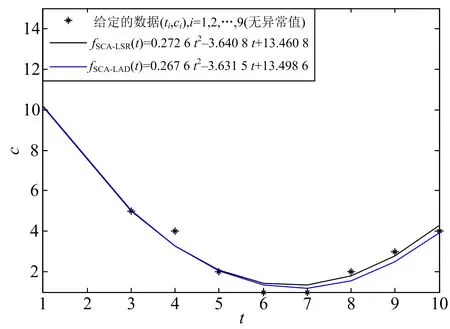
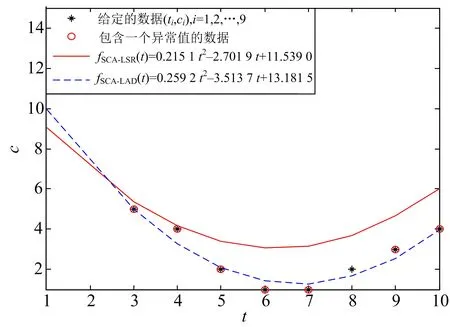
while(t

fori=1 toNdo//对每一个个体进行更新

forj=1 toDdo//对每一维上进行更新

根据式r1=a-at/Tmax计算r1的值;

随机产生r2∈U[0,2π],r3∈U[0,2],r4∈U[0,1];

ifr4<0.5

(5)

else

(6)

end if

end for

end for

越界处理;

计算每个个体的适应值并更新种群的最优个体位置P(t);t=t+1;

end while.

SCA算法最显著的特点是基于正弦函数(5)和余弦函数(6)值的变化来达到寻优目的,其结构简单,容易实现.在SCA算法中,主要参数有r1,r2,r3,r4,最关键的参数r1控制算法从全局搜索到局部开发的转换.更多SCA算法详见文献[16-22].

3 算 例

给定的数据见表1,2,表1中的数据无异常值,表2中的数据包含一个异常值.对表1,2中的数据分别采用最小二乘和最小一乘.算法程序用Matlab R2009a编写.为消除随机数对算法的影响,SCA算法运行10次后,选取最优结果(即误差最小)进行拟合.SCA算法参数设置:种群规模N=30,控制参数a=2,最大迭代次数Tmax=2 000,搜索空间为[-5,15]3.

算例已知某因变量c与自变量t满足的关系式为

c=x1t2+x2t+x3≜f(t,X),

其中:X=(x1,x2,x3)是待定参数.对变量c,t观测9次,得到的数据如表1所示.

表1 给定的数据(无异常值)

建立优化模型为

(7)

(8)

模型(7)采用最小二乘,模型(8)采用最小一乘.模型(7)采用SCA算法得到最优解XLSR=(0.272 6, -3.640 8, 13.460 8).模型(8)采用SCA算法得到最优解XLAD=(0.267 6, -3.631 5, 13.498 6).两种方法的拟合曲线如图3所示.

由于一个错误输入数据,得到含有异常值的数据,见表2.

表2 含有1个异常值的数据

图3 无异常值的非线性最小二乘与最小一乘拟合结果

图4 有异常值的非线性最小二乘与最小一乘拟合结果

表3给出了详细的拟合值与误差.

表3 SCA算法计算结果

从上述结果来看:无异常值时,最小二乘与最小一乘得到的结果相差不大;有异常值时,最小二乘的结果偏向异常值,而最小一乘变化较小,这充分表明异常值对最小二乘有着比较大的影响,而对最小一乘的影响较小.这主要是因为:当数据中含有异常值时,异常值有较大的偏差,其平方值(几何意义即面积)相对更大.为了“优化”平方和,就不能不“将就”这些点,因而增加了残差大的数据对拟合曲线的影响,使得异常值会把拟合曲线拉得离异常值更近一些,导致拟合结果失真.因此,对含有异常值的数据进行拟合时,应选择最小一乘以减少异常值对拟合结果的影响.