线性差分方程的周期解
2023-05-22尤卫玲张更容
王 琦,尤卫玲,张更容
(1.广东开放大学 公共课教学部,广东 广州 510091;2.湖南第一师范学院 数学与统计学院,湖南 长沙 410205)
在某种程度上来讲,差分方程是微分方程的离散化,在自然科学和社会科学中,很多涉及离散变量的实际问题中都可通过建立差分方程模型加以解决. 虽然差分方程看似简单,但有些差分方程的动力学性质至今也没有得到完全解决. 文献[1-2]中作者分别研究了2,3阶有理差分方程,对解的有界性、周期性、全局稳定性以及解的存在性等做了系统的探讨和总结,提出了许多猜想和公开问题,但这些猜想和公开问题只得到了部分解决[3-4],仍有很多悬而未决.
学者很少对差分方程多周期解进行探讨,即使对微分方程多周期解[5]的讨论也很少. Moaaz等[6]研究了差分方程
Jn+1=aJn-1e-f(Jn,Jn-1),n=0,1,2,…
解的渐近行为,其中a为正数;给出了方程存在二周期解的充分必要条件,以及解为终于2k周期解的充分条件,但未证明多周期解的局部渐近稳定性. 有关差分方程的最新研究成果,可参阅文献[7-10].
文献[11]中作者考察了线性差分方程
xn+1=a1xn+a2xn-1+…+akxn-k+1,n=0,1,2,…,
(1)
记
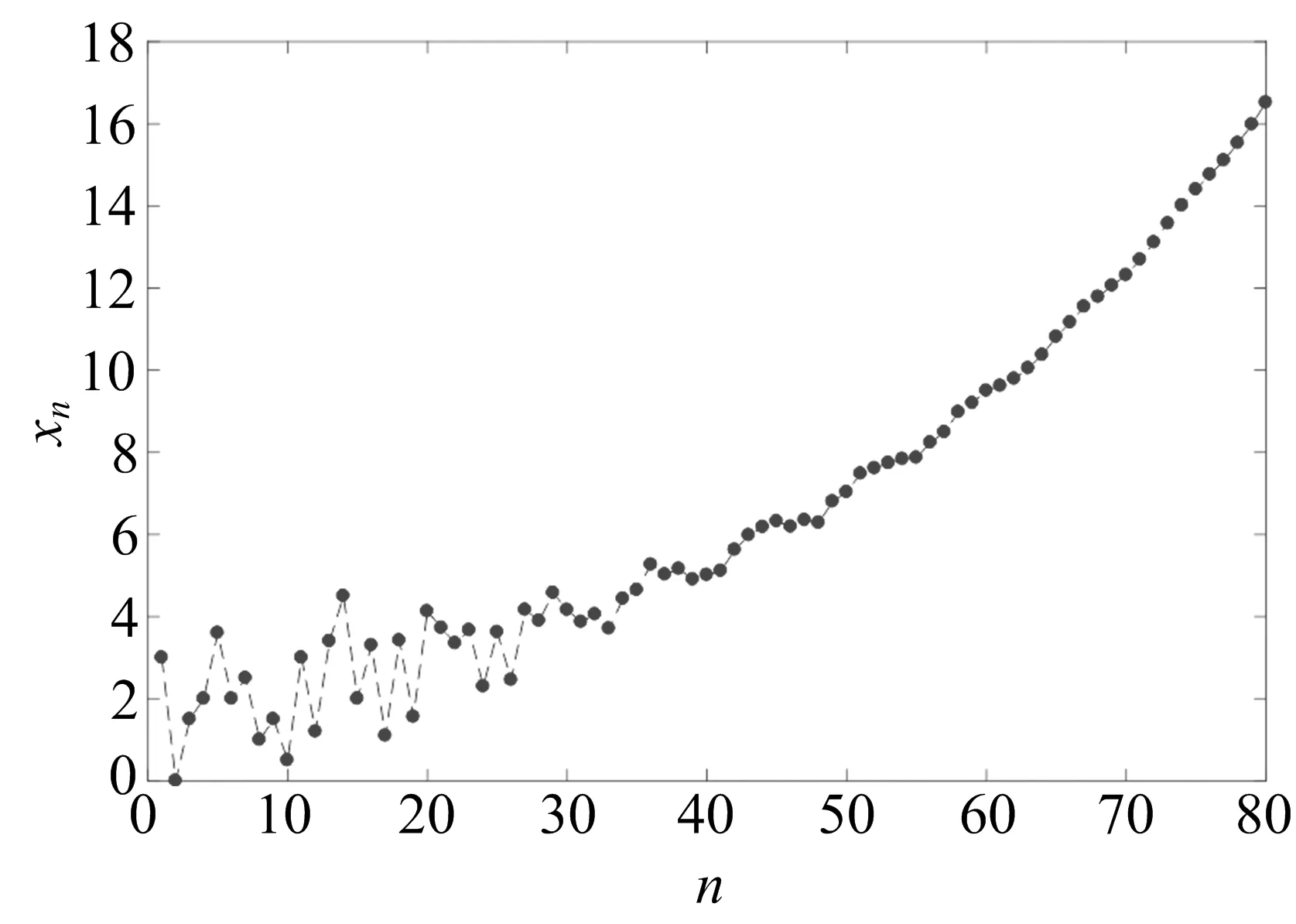
其中:r=i1 设(i1,i2,…,im)=d,(i′1,i′2,…,i′m)=1,is=i′sd,s=1,2,…,m. 在文献[11]中,有如下假设: (H) 对任意t∈{0,1,…,r-1},存在i∈X,s∈{0,1,…,k},使得t=i-sr. 在此前提下,得到了如下结论: (1) 当且仅当q≤1时,差分方程(1)的任意非负解收敛于差分方程(1)的零平衡点. (2) 当且仅当q>1时,差分方程(1)的任意非负非零解均为无界解,事实上都收敛于无穷大. 作者研究在q=1的情形下差分方程(1)的周期解,结合文献[5]中的结论,得到差分方程(1)具有如下三分法特征: (1) 当且仅当q<1时,差分方程(1)的任意非负解收敛于差分方程(1)的零平衡点. (2) 当且仅当q=1时,差分方程(1)的任意非负解收敛于差分方程(1)的一个d-周期解. (3) 当且仅当q>1时,差分方程(1)的任意非负非零解均为无界解,事实上都收敛于无穷大. 论文证明方程多周期解的存在性以及多周期解的局部稳定性的方法,为研究一般差分方程的多周期解提供了一种思路. 定理1当且仅当q=1时,差分方程(1)存在素d-周期解. 证明设q=1.若d=1,显然差分方程(1)存在平衡点,故结论成立. 因而不妨假设d>1,差分方程(1)可简写为 xn+1=ai1xn-i1+1+ai2xn-i2+1+…+aimxn-im+1,n=0,1,2,…. (2) 因为q=1,所以 取初始值 x-im+l+jmd=x-im-1+l+jm-1d=…=x-i2+l+j2d=x-i1+l+j1d=φl, (3) 其中:l=1,2,…,d,js=0,1,…,i′s,s=1,2,…,m,φi≠φj,i≠j. 以下规定φ0=φd.于是由(2)式可知 ⋮ 不难证明,对任意n≥1,有xn=φnmodd,注意到φi≠φj,i≠j,因而由初始值(3)得到的解即为差分方程(1)素d-周期解. 另一方面,若差分方程(1)存在素d-周期解φ1,φ2,…,φd,φ1,φ2,…,φd,…,则存在l∈{1,2,…,d},使得φl≠0,因为d|is,s=1,2,…,m,所以由(2)式知 引理1当q=1时,差分方程(1)的非负解均是有界的. ⋮ 定理2当且仅当q=1时,差分方程(1)的非负解收敛于差分方程的一个d-周期解. 证明设q=1.若m=1,此时d=r=i1=k,差分方程(1)可简化为 xn+1=xn-d+1, 显然此时方程的解均是d-周期解,故也收敛于d-周期解. 设m>1,因为 (i1,i2,…,im)=d,(i′1,i′2,…,i′m)=1,is=i′sd,s=1,2,…,m, 所以存在非零整数λ1,λ2,…,λm,使得 λ1i′1+λ2i′2+…+λmi′m=1. 记h=k(|λ1|i1+|λ2|i2+…+|λm|im)=k(|λ1|i′1+|λ2|i′2+…+|λm|i′m)d,则对于任意i=1,2,…,k,有 h+id=[(k|λ1|+iλ1)i′1+(k|λ2|+iλ2)i′2+…+(k|λm|+iλm)i′m]d. 结合差分方程(2)可知 ai1φl,i1+ai2φl,i2+…+aimφl,im≤ai1φl+ai2φl+…+aimφl=qφl=φl. 因而φl,is=φl,l=1,2,…,d,s=1,2,…,m.归纳可得,对任意0≤ps≤2kλs,s=1,2,…,m,有 因此对于任意i=1,2,…,k,有 (4) 对于任意ε>0,由(4)式知,存在正整数Ni,对于任意i=1,2,…,k,当jNi>Ni时,有 |xnl,jNid+l-(h+id)-φl|<ε. 令u=max{N1,N2,…,Nk},则 |xnl,ud+l-(h+id)-φl|<ε. 注意到 xnl,ud+l-h=a1xnl,ud+l-h-1+a2xnl,ud+l-h-2+…+akxnl,ud+l-h-k= ai1xnl,ud+l-h-i1+ai2xnl,ud+l-h-i2+…+aimxnl,ud+l-h-im= ai1xnl,ud+l-(h+i′1d)+ai2xnl,ud+l-(h+i′2d)+…+aimxnl,ud+l-(h+i′md), 因此 |xnl,ud+l-h-φl|≤ai1|xnl,ud+l-(h+i′1d)-φl|+ ai2|xnl,ud+l-(h+i′2d)-φl|+…+aim|xnl,ud+l-(h+i′md)-φl|< ai1ε+ai2ε+…+aimε=qε=ε. 归纳可得,对于任意n>nl,u-k(|λ1|i′1+|λ2|i′2+…+|λm|i′m+1),有|xnd+l-φl|<ε.即对任意ε>0,存在 Ml=nl,u-k(|λ1|i′1+|λ2|i′2+…+|λm|i′m+1), 当n>Ml时,有|xnd+l-φl|<ε,因此 由差分方程(1)可知 xnd+l=a1xnd+l-1+a2xnd+l-2+…+akxnd+l-k, 在方程两端令n→∞,取极限得 φl=φ(l-1+imd)modd+φ(l-2+imd)modd+…+φ(l-k+imd)modd, 另一方面,由定理1显然成立及综上所述,结论得证.接下来考察假设(H)与d的关系. 命题1设r,j1,j2,…,jr-1是模r的一个完全剩余系,则(r,j1,j2,…,jr-1)=1. 证明设r,j1,j2,…,jr-1是模r的一个完全剩余系,不妨设i≡ji(modr),i=1,2,…,r-1,于是存在s1,s2,…,sr-1∈,使得 ji=sir+i,i=1,2,…,r-1. (5) 设(r,j1,j2,…,jr-1)=d,于是d|r,d|ji,i=1,2,…,r-1.由(5)式知,d|i,i=1,2,…,r-1,从而d|(1,2,…,r-1),而(1,2,…,r-1)=1,所以d=1,即(r,j1,j2,…,jr-1)=1. 命题2假设(H)成立,则d=1. 证明设假设(H)成立,即对任意t∈{0,1,…,r-1},存在i∈X,s∈{0,1,…,k},使得t=i-sr,即i=t+sr.不妨设 ip1=1+s1r,ip2=2+s2r,…,ipr-1=r-1+sr-1r, 其中:ip1,ip2,…,ipr-1∈X,s0,s1,…,sr-1∈{0,1,…,k},显然r,ip1,ip2,…,ipr-1是模r的一个完全剩余系. 由命题1知 (r,ip1,ip2,…,ipr-1)=1, 注意到{r,ip1,ip2,…,ipr-1}⊆{i1,i2,…,im},因而(i1,i2,…,im)|(r,ip1,ip2,…,ipr-1),即d|1,所以d=1. 注命题2的逆命题不成立,即d=1时假设(H)未必成立. 例如,对于差分方程 xn+1=0.4xn-3+0.1xn-4+0.5xn-6,n=0,1,2,…, 此时X={4,5,7},d=(4,5,7)=1,r=4,k=7,而对于t=2∈{0,1,2,3},显然找不到i∈X,s∈{0,1,…,7},使得t=i-sr,即假设(H)不成立. (1) 差分方程 xn+6=0.25xn+5+0.1xn+3+0.15xn+1+0.2xn,n=1,2,3,…, (6) 取初值 [x1,x2,x3,x4,x5,x6]=[0.5,3.2,1.5,2,1.6,1.7], (2) 差分方程 xn+15=0.1xn+9+0.5xn+6+0.4xn,n=1,2,3,…, (7) 取初值 [x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15]= [3,0,1.5,2,3.6,2,2.5,1,1.5,0.5,3,1.2,3.4,4.5,2], 图1 非负解收敛于方程的零平衡点 图2 非负解收敛于方程的3-周期解 (3) 差分方程 xn+12=0.2xn+4+0.8xn,n=1,2,3,…, (8) 取初值 [x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]=[3,0,1.5,2,3.6,2,2.5,1,1.5,0.5,3,1.2], (4) 差分方程 xn+15=0.4xn+13+0.6xn+6+0.2xn,n=1,2,3,…, (9) 取初值 [x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15]= [3,0,1.5,2,3.6,2,2.5,1,1.5,0.5,3,1.2,3.4,4.5,2], 图3 非负解收敛于方程的4-周期解 图4 非负解收敛于无穷大 由命题2和注记可以看出,文献[5]的结论是论文结论的一个特例,论文还给出了线性差分方程非负解收敛于周期解的一个充分必要条件. 结合文献[5]以及论文的结论,证得了差分方程(1)具有三分法特征.1 主要结果
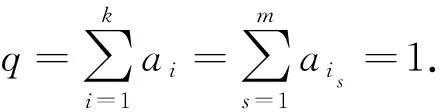
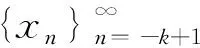
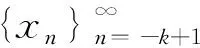
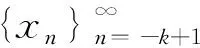
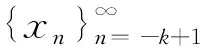
2 数值模拟
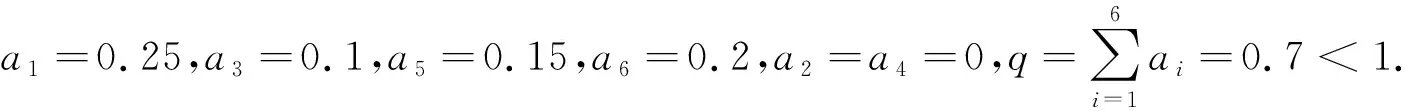
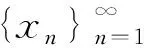
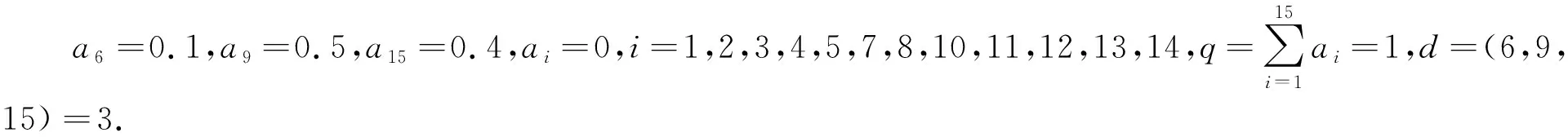
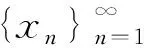
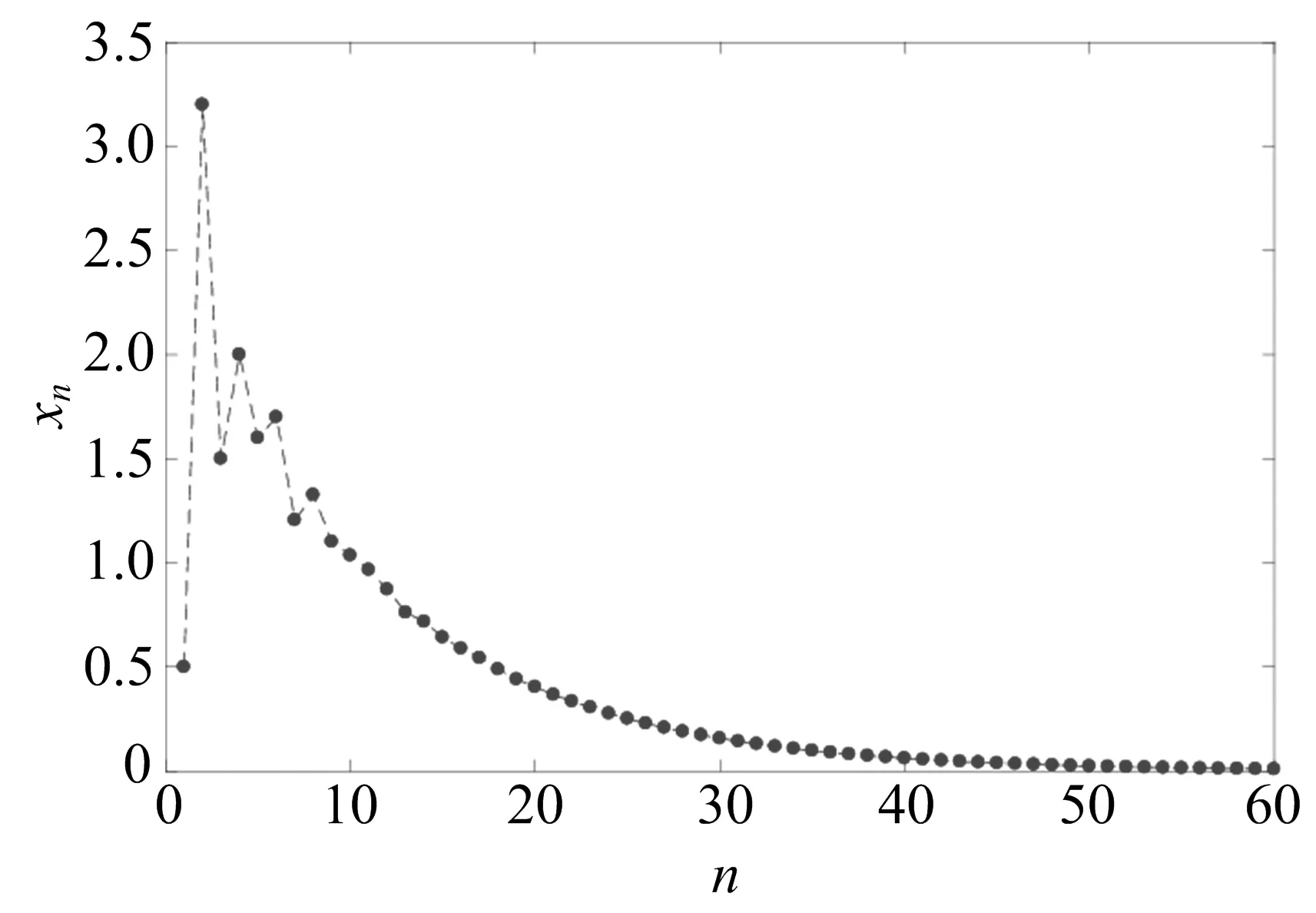
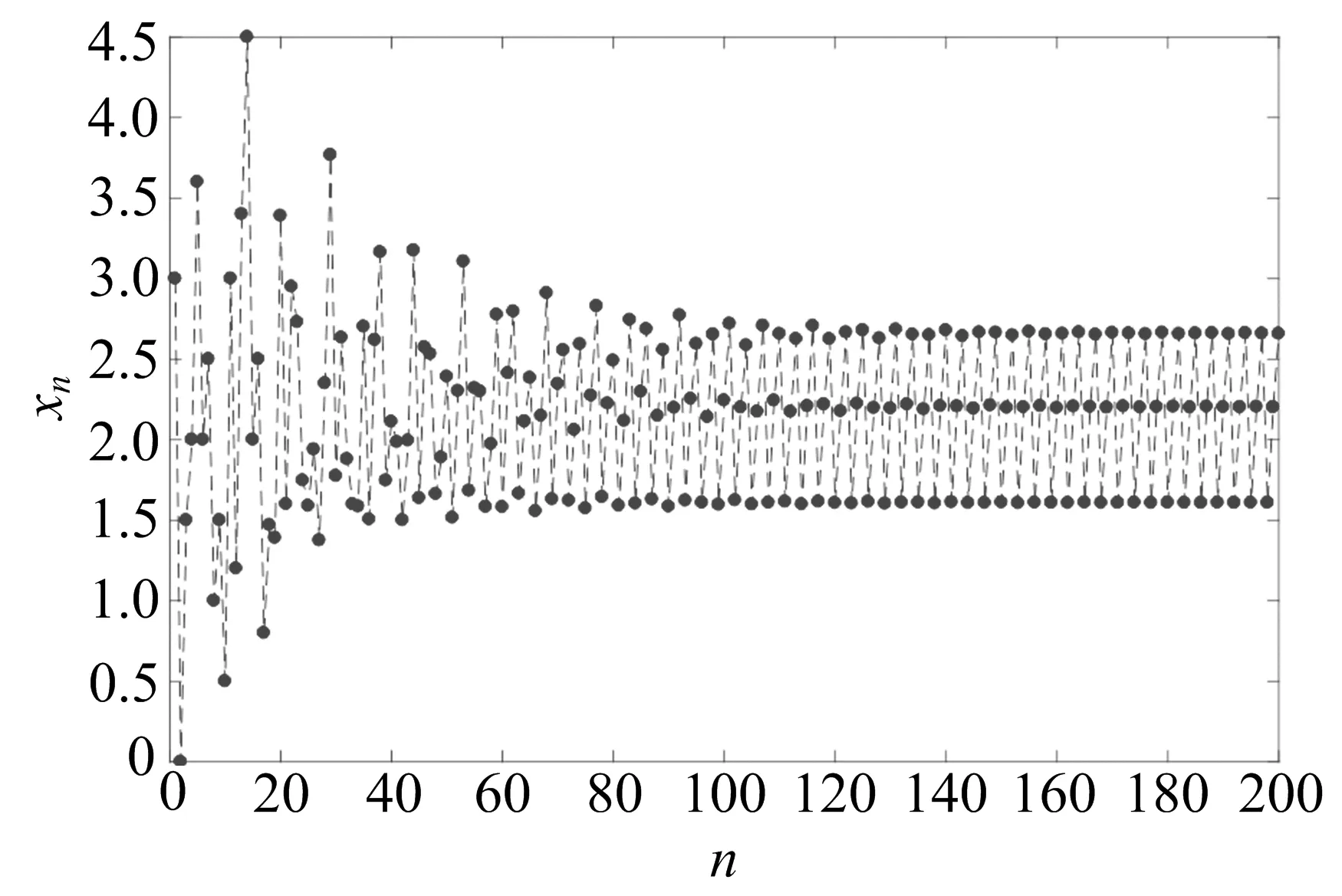
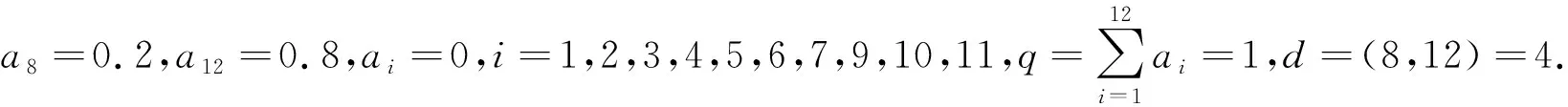
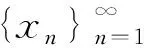
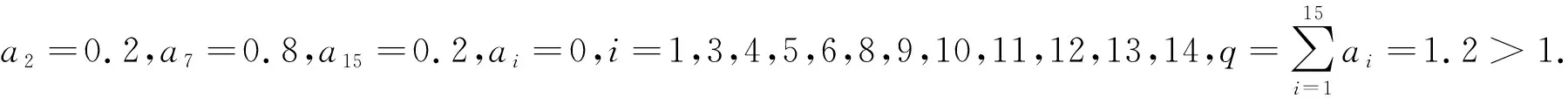
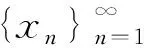

3 结束语
