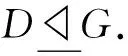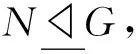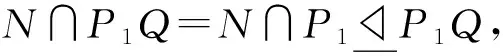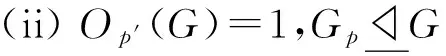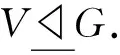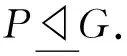准素数子群的δ-置换性对有限群结构的影响

高建玲,毛月梅,曹建基

(1.山西大同大学 数学与统计学院,山西 大同 037009;2.山西财经大学 应用数学学院,山西 太原 030006)

论文中所讨论的群皆为有限群,G表示群,p表示素数,π表示由素数构成的集合,π(G)表示由|G|的所有素因子构成的集合.所用符号和术语皆为标准的,见文献[1-3].

2003年,Asaad等在文献[4]中引入了子群的δ-置换性.设δ为G的Sylow子群完全集,即对每一个p∈π(G),δ仅包含G的一个Sylowp-子群Gp.设H≤G,称H在G中δ-置换,若H置换δ中每个元素.通过研究G的素数阶子群的δ-置换性,得到了一些有趣的结论.Heliel等[5]证明如下结论: 令δ是G的Sylow子群的完全集,若对每一个Gp∈δ,Gp的每个p阶或4阶(p=2)循环子群在G中δ-置换,则G是超可解的. Li等[6]得到结论: 若p是|G|的最小素因子,Gp的极大子群在G中δ-置换,其中Gp∈δ,则G是p-幂零的. Li等[7]证明了: 若P的每个p阶或4阶(p=2)循环子群在G中δ-置换,其中p是|G|的最小素因子,P是Sylowp-子群且P∈δ,则G是p-幂零的. Heliel等[8]讨论了δ-置换子群的嵌入及δ-置换性对有限群结构的影响.

论文将进一步讨论δ-置换子群对有限群结构的影响,并推广以上结论.

1 预备知识

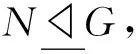
定义[9]设K,H≤G,δ是H的Sylow子群的完全集,称K在H中δ-置换,若K置换δ中的每个元素.

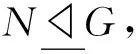
(1)δ∩N及δN/N分别是N及G/N的Sylow子群的完全集;

(2)UN/N是G/N的δN/N-置换子群;

(3) 若U≤N,则U是N的δ∩N-置换子群.

引理2[1]如果|G|=pαqβ,则G可解.

引理3[10]设N是群G的一个非平凡正规子群,若N∩Φ(G)=1,则F(N)为G的极小正规子群直积.

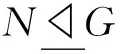
下面介绍一下文中用到的一些关于群系的基础知识．群的集合F称为群类,如果当这个集合包含群G时,它也包含所有与G同构的群．当群G属于群类F时,称G是F-群．如果一个群类F满足以下两个条件:

(1) 当G∈F时,对于G的任意正规子群N,有G/N∈F;

(2) 当G/N1∈F,G/N2∈F时,有G/(N1∩N2)∈F,其中N1,N2为G的两个正规子群,则称F是一个群系．

一个群系F称为饱和的,如果G/Φ(G)∈F时,总有G∈F.对于一个群系 ,群G的所有使G/N∈F的正规子群N之交称为G的F-剩余,记为GF．显然G/GF∈F且GF是G的特征子群．文中用N表示所有幂零群组成的群系.

论文将给出有限群为p-幂零群、p-超可解群、超可解群的一些结论.

2 主要结论

定理1设p是|G|的素因子,P∈Sylp(G),H是G的p′-Hall子群,满足G=PH.令δ是H的Sylow子群的完全集,若G满足以下条件:

(1)NG(P)是p-幂零的;

(2)P的每个极大子群在H中δ-置换.

则G是p-幂零的.

证明假设定理不成立,G为极小阶反例.分以下几步证明定理:

(1) 设Q∈Sylq(H).显然,若G1=PQ≤G,则NG1(P)是p-幂零的.

(2)Op′(G)=1.

若Op′(G)≠1.因为NG/Op′(G)(POp′(G)/Op′(G))=NG(P)Op′(G)/Op′(G)是p-幂零的,由引理1 (2)知G/Op′(G)满足定理条件.因此由G的极小性可得G/Op′(G)是p-幂零的,从而G是p-幂零的,矛盾.故Op′(G)=1.

(3)G=PQ,其中Q∈Sylq(G)且q≠p.因此|π(G)|=2且|G|=pαqβ.

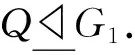
(4) 得出矛盾.由(3)和引理2可得G可解.再由(2)知Op(G)≠1,令N是G的极小正规子群且满足N≤Op(G).由引理1 (2)知商群G/N满足定理条件,由G的极小性可得G/N是p-幂零的.由于所有p-幂零群组成的群系是饱和群系,所以N是G唯一的极小正规子群且N≤/Φ(G).由引理3可知Op(G)=N=F(G)是初等交换p-群.故存在G的极大子群L满足G=NL且N∩L=1.因此P=N(P∩L)且P∩L=P*∈Sylp(L).如果P*=1,则P=N,所以G=NG(N)=NG(P)是p-幂零的,矛盾.现假设P*≠1.显然P*≠P,取P的极大子群P1满足P*≤P1,由假设知P1在H中δ-置换.因L的Sylowq-子群是H的Sylowq-子群,对Q∈Sylq(L)且Q∈δ,有P1Q=QP1,又N≤>/P1,所以P1Q

注1在定理1中,条件“NG(P)是p-幂零的”不能去掉.例如,取G=S3,p=3.因为S3的Sylow 3-子群P是3阶循环群,所以P每个极大子群置换S3的Sylow 2-子群,但是S3不是3-幂零的.

定理2设p是|G|的素因子,P∈Sylp(G),H是G的p′-Hall子群满足G=PH.令δ是H的Sylow子群的完全集,若(|G|,p-1)=1且P的每个极大子群在H中δ-置换,则G是p-幂零的.

证明假设结论不成立,并设G为极小阶反例.分以下几步证明定理:

(1)Op′(G)=1.若Op′(G)≠1,显然(|G/Op′(G)|,p-1)=1且POp′(G)/Op′(G)∈Sylp(G/Op′(G)),由引理1(2)可知,G/Op′(G)满足定理条件.因此由G的极小性可得G/Op′(G)是p-幂零的,从而G是p-幂零的,矛盾.故Op′(G)=1.

(2)P不循环.如果P循环,那么P≤CG(P)≤NG(P)且|NG(P)/CG(P)|是p′-数.由N/C定理有NG(P)/CG(P)Aut(P)且|Aut(P)|=pn-1(p-1),所以NG(P)=CG(P),那么由Burnside定理可得G是p-幂零的,矛盾.故P不循环.

(3)G=PQ,其中Q∈Sylq(G)且q≠p.因此|π(G)|=2且|G|=pαqβ.

类似定理1的(3)的证明,可得结论.

注2在定理2中,条件“(|G|,p-1)=1”不能去掉,例子同注1.

文献[12]中,引入了PΣT-群: 称G是PΣT-群,若G=DC是超可解的,其中D=GN是G的奇数阶幂零Hall子群且它的所有极大子群在G中正规.下面将通过子群的δ-置换性刻画PΣT-群.

定理3假设G是可解群,δ是G的Sylow子群的完全集.若G的所有Sylow子群的每个极大子群在G中δ-置换,则G=DC是超可解的,其中D=GN是G的一个奇数阶幂零Hall子群且它的所有极大子群在G中正规.

证明假设定理不成立,取G为极小阶反例.分以下几步证明定理:

设P/N∈Sylp(G/N)且M/N是P/N的极大子群,其中p是|G/N|的任一素因子,则存在Gp∈Sylp(G)满足P=GpN且M∩Gp是Gp的极大子群.显然M/N=(M∩Gp)N/N.由引理1(2)知M/N在G/N中δN/N-置换,这表明G/N满足定理条件,因此G/N=DN/NC/N是超可解的,其中DN/N=(G/N)N是G/N的一个奇数阶幂零Hall子群且它的所有极大子群在G/N中正规.

(3)D是G的幂零Hall子群.由(2)知G′是幂零的,因此D=GN是幂零的.下证D是G的Hall子群.如果D不是G的Hall子群,则G≠D≠1.取P∈Sylp(D)满足1

(i) 若N是G的极小正规子群且N≤D,则N=Op(D)=P是D的Sylowp-子群.因为N是G的极小正规子群且N≤D,由(2)知N是素数幂阶群.假设|N|=qn,其中q∈π(D)且p≠q.由(1)知,D/N=(G/N)N,G/N的Hall子群.因为PN/N∈Sylp(D/N),所以PN/N∈Sylp(G/N),故P∈Sylp(G),矛盾.从而p=q且N=Op(D)=P.

(iv) (3)的最后矛盾.

(5) |D|是奇数.若2∈π(D),则D有极大子群M满足|G/M|=2.所以G/M=CG(D/M)且D/M≤Z(G/M),故G/M是幂零的,D≤M,矛盾.因此|D|是奇数.

(2)～(5)表明定理结论对G成立,与G的选取矛盾.因此结论成立.