一道竞赛题的推广与探究*

广东省佛山市南海外国语学校 (528200) 李辉义

安徽师范大学数学与统计学院 (241000) 曹明响

1 引言

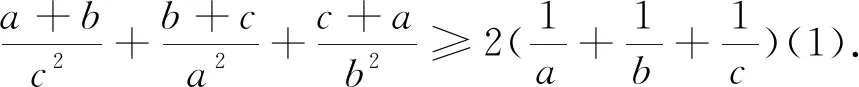
文[1]给出了其一个命题及推论,下面利用切比雪夫不等式进行统一推广,并给出该试题的另一个推广.

2 一个引理

为了方便证明,先给出如下引理.

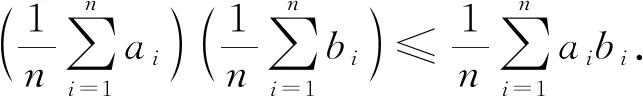
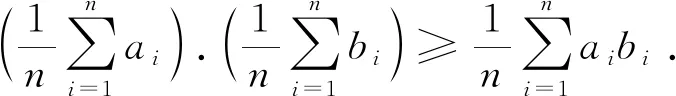
3 不等式(1)的探究与推广

先给出此不等式(1)的一个简证.

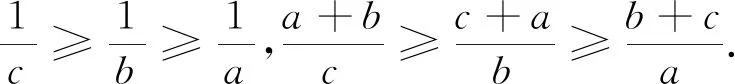
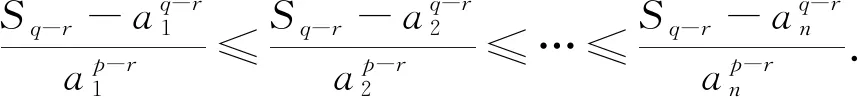
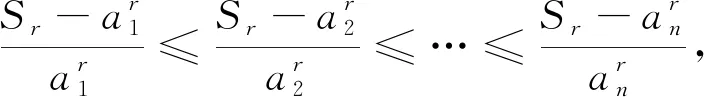
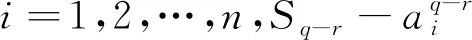
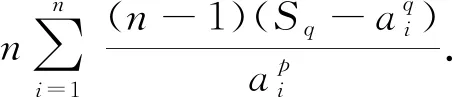
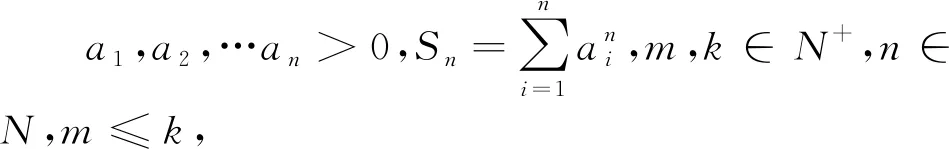
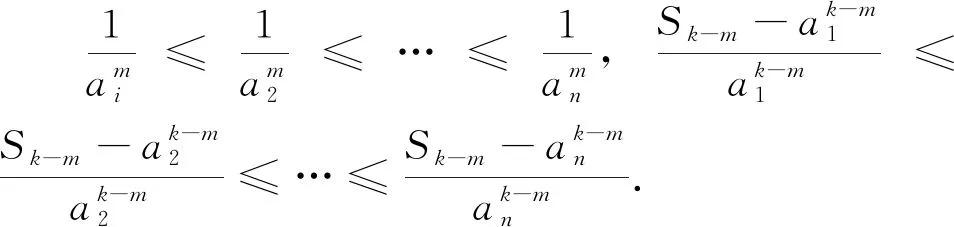
令n=3,k=2,m=1即得罗马尼亚竞赛题.

4 问题拓展

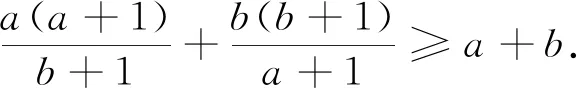
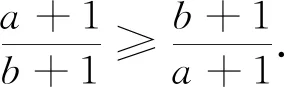
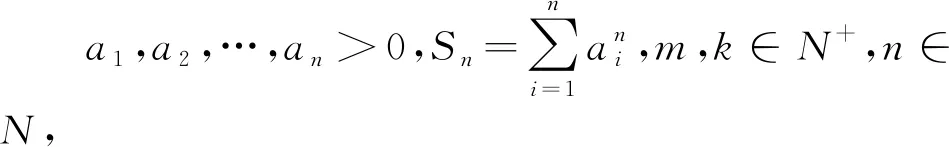
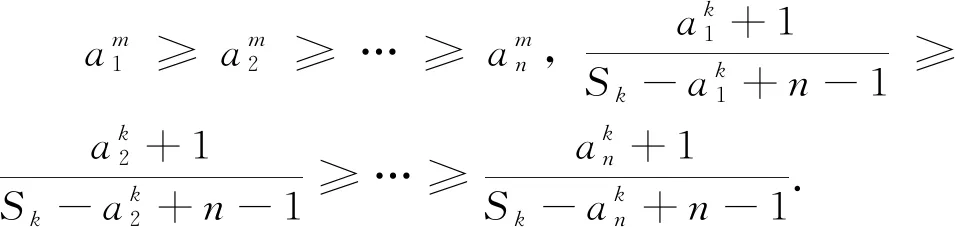
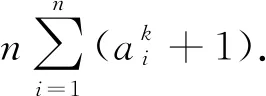
令m=k=1,n=2即得科索沃竞赛题.