三大策略破解圆锥曲线中一类“非对称”结构

江苏省南京市第九中学 (210018) 竺宝林

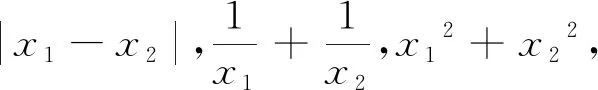
1 问题呈现

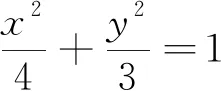
2 问题解决

策略一转化为“对称”结构

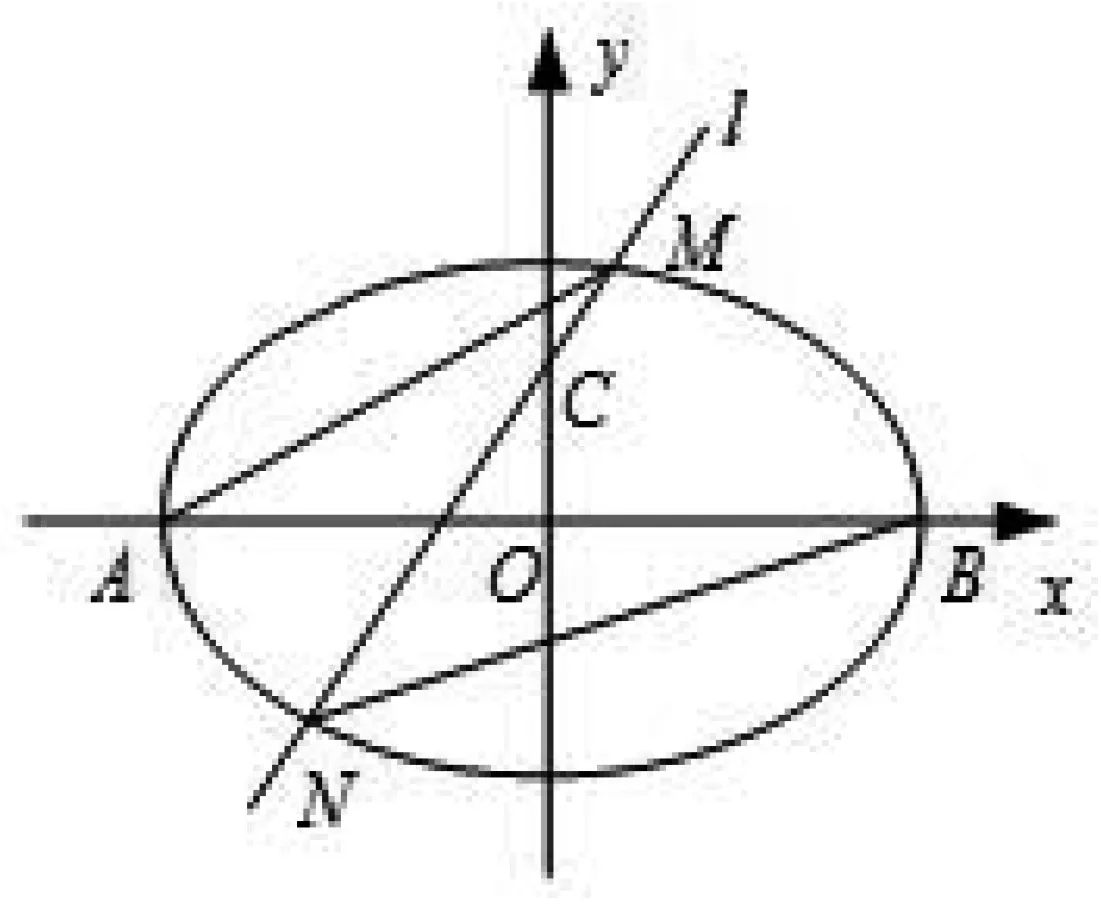
图1

解法1：(平方曲化,利用曲线转化)由椭圆的对称性可知直线l的斜率一定存在,设其方程为y=kx+1,设M(x1,y1),N(x2,y2).

联列方程组

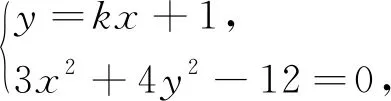
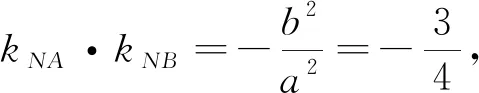
评注：化“非对称结构”为“对称结构”应该是非常自然的想法,这也体现了数学中化归思想方法的运用.

策略二利用韦达定理消元

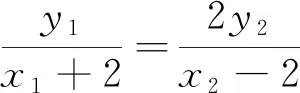
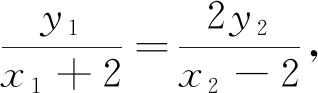
评注：解析几何的本质是用代数方法研究几何图形的性质,将几何问题转化为代数问题,其中包含了较为复杂的代数运算,如何处理这些复杂的运算,消元与减元是关键.

策略三运用三点共线

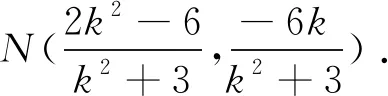
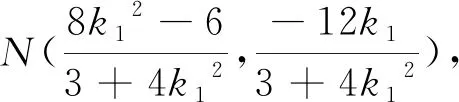
所以(8k12+ 3)(8k12+ 6k1-3) = 0,则8k12=

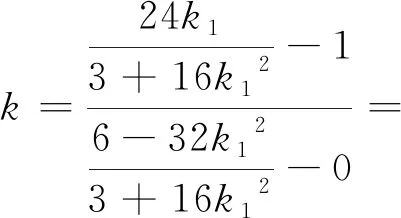
评注：解决解析几何问题,除了要应对代数运算,还要学会从几何图形中分析其几何特征,只有将几何特征分析得非常充分,代数化才能更加简洁,代数运算的难度才能降低.