一道双曲线高考试题的解法探究与变式*

江苏省海门中学 (226100) 徐巧石

高考试题凝聚着命题专家们的深度思考,能够考查学生的思维品质、关键能力,发挥了数学学科高考的选拔功能,对中学数学教学起到了积极的引导和促进作用．于参加高考的学生而言,是对他们能力、素养的一次全面考查;于高一高二的学生而言,是提升他们能力,发展数学素养的良好素材;于教师而言,是研究教学、实践命题的丰富源泉．因此,加强高考真题的研究,深度理解,发挥试题的应用价值是必要和有积极意义的课题．

1．审读目标条件

(1)求C的方程;

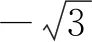
①M在AB上;②PQ∥AB;③|MA|=|MB|．

注:若选择不同的组合分别解答,则按第一个解答计分．

今年是新高考的第二年,新高考在命题上创新试题形式,引导高中教学向培养核心素养和数学能力倾斜,同时增强了试题的开放性．此题是结构不良问题的再创新,避开各地的模拟题,体现了公平性．题目给出三个条件,要求从中选取两个作为已知条件,证明另一个成立,为学生提供了选择的自由度和发挥的空间,有利于考查学生的思维水平．从试题结构看,体现了三多,即点多、线多、变量多,如何在众多的关系中寻找解决问题的主线?如何挖掘条件背后隐含的关系?如何确定解题的方向?试题目背后存在怎样的一般规律?

2．探索解题方向

解决任何问题首先要有明确的目标,有了目标才有前进的方向和信心．解题教学要将重点放在目标的确定上,教会学生探索解题方向的方法．常见的寻找解题方向的方法有特殊值探路、数形结合引领、题目设问导向等等．

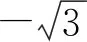
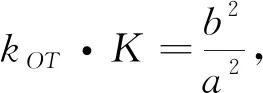
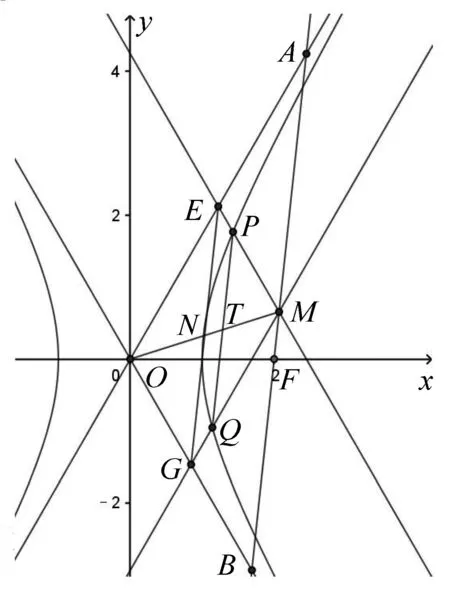
图1

在解题教学中,特别是讲解有一定难度的题目,要通过问题引领带领学生,探索解题的目标方向,而不应对着答案照本宣科．在经历一道道试题的探索过程中,让学生掌握探索解题方向的常用方法,积累探索解题方向的基本经验．探索解题目标与方向是提升学生思维水平,直观想象数学素养的具体表现．

3．梳理解题思路

2020年《普通高中数学课程标准》中提出“数学运算”核心素养,包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等．解题有了目标,接下来便是探究思路,按照既定的方向通过运算说明目标成立．．

实现第一目标,有以下三种思路:

思路二：注意到点M是连接PQ和AB之间的关键点,可以对题干重新叙述,即从M点出发作两条平行于渐近线的直线,与双曲线C产生交点P,Q,进而证明PQ的斜率与点M坐标之间的关系．

思路三：根据2中探究解题思路的思考,首先证明EG∥PQ,进而说明OM经过PQ的中点T,再根据弦的中点,利用点差法建立M与PQ之间的关系．

实现第一目标之后,从三个条件中选择两个作为已知条件,证明另一个成立,共有三种情形,即由①②证③;由①③证②;由②③证①,分别对应以下图2,图3,图4三种思路:

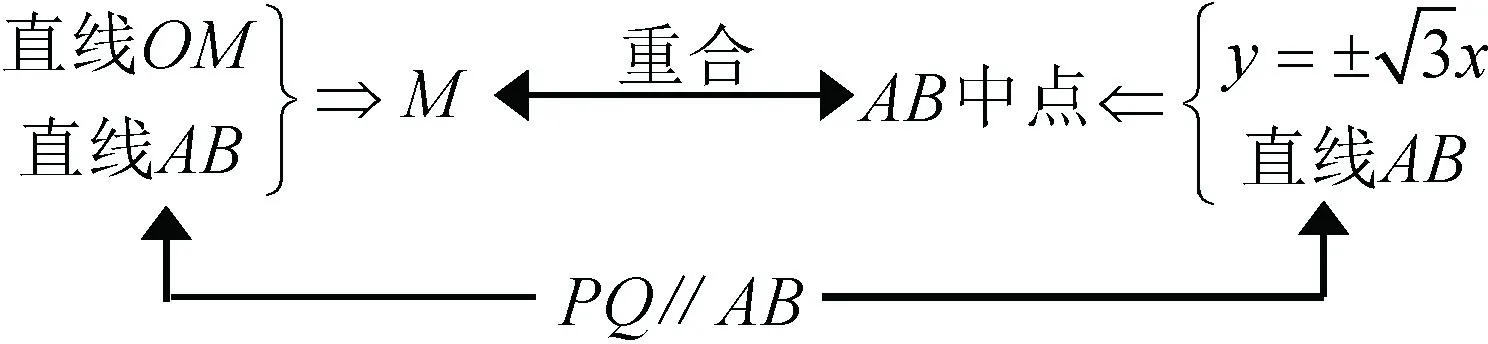
图2

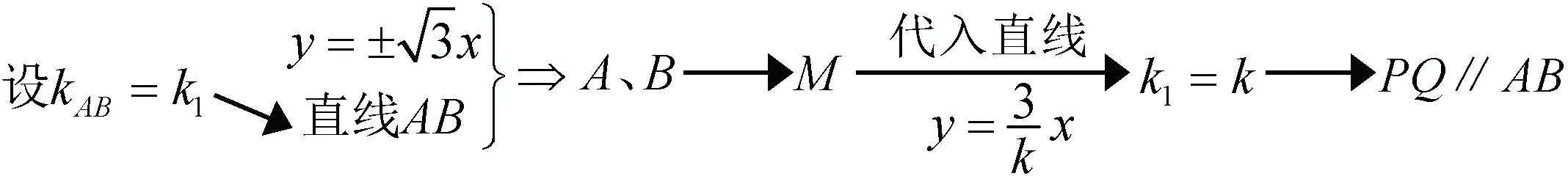
图3

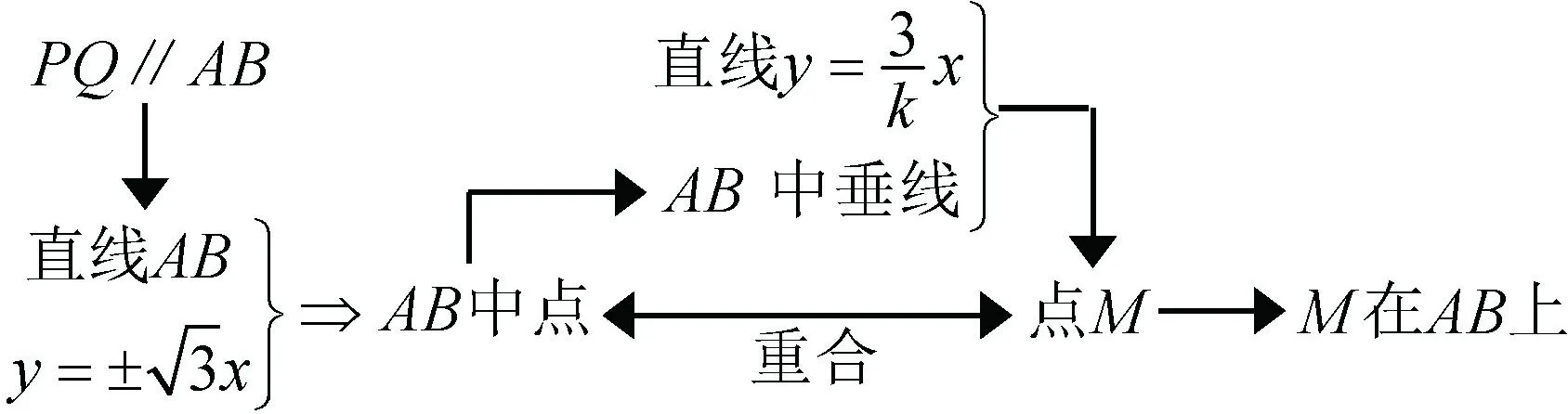
图4

4．实施调整运算

设计好了解题的思路,接下来就是将思路付出实践,在实践的过程中,调整细化具体的运算方法、技巧,选择最简最优策略．

法一：由思路一和选择①②证③．

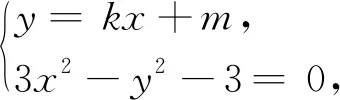
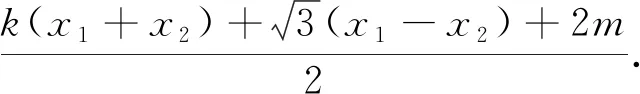
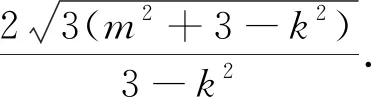
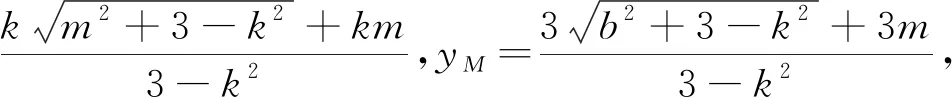
上述化简M坐标的过程中,涉及到了x1-x2,这里采用的是用x1+x2与x1x2表示x1-x2.若不是x1-x2,系数发生变化,又该如何处理呢?注意到这是不对称的结构,一般的处理方法是保留其中一项,将其余化为x1+x2与x1x2,因此有如下处理方式:

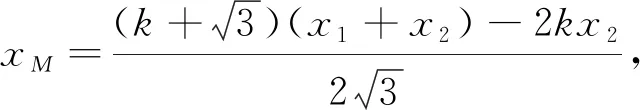
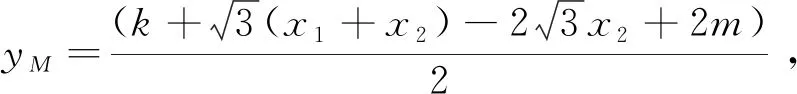
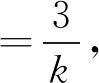
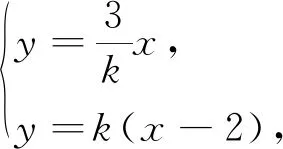
在运算的细节处理上,既要有硬算的勇气,又要学会一般的处理技巧,学会识别常见的运算模型,引导学生掌握一般的方法,在运算方法的选择与调整中,提高学生发现问题和解决问题的能力．

法二：由思路二和选择①③证②．

设M(x0,y0),P(x1,y1),Q(x2,y2),联立

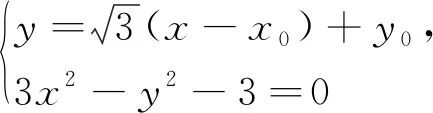
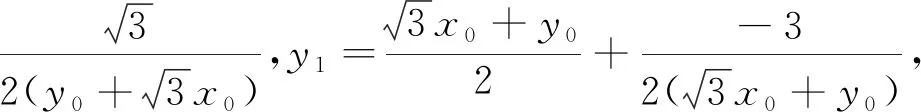
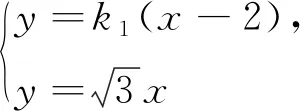
此法第一目标的处理看似简洁,实际上需要学生扎实的运算功底,同时又要有运算下去的信心．注意到直线PM与渐近线是平行的,可以直线PM与双曲线C必有唯一一个交点,并且可以预见联立方程消去y可得一个一元一次方程,从而获得运算成功的信心．

法三：由思路三和选择②③证①．

设直线PQ:y=kx+m,联立

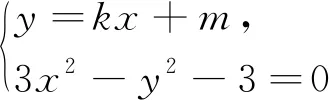
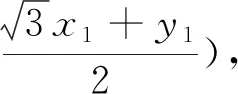
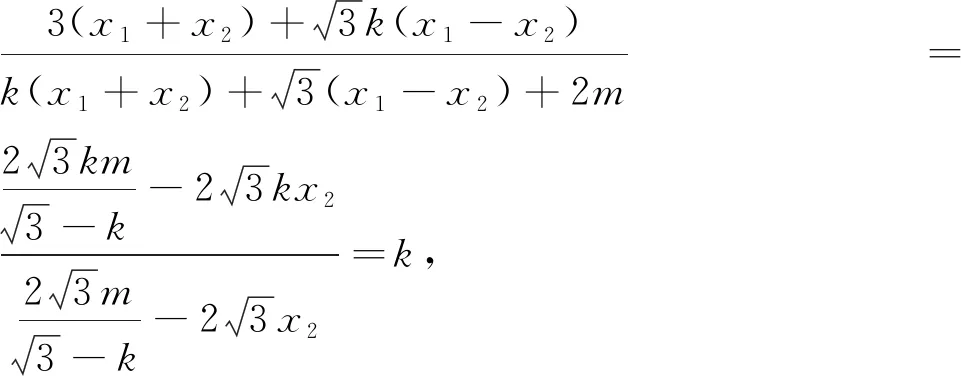
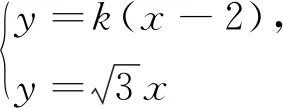
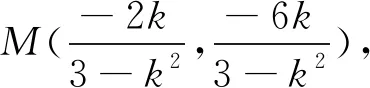
此法,第一目标的处理看上去繁琐,但是有着非常清晰的逻辑主线,避免了复杂的运算,也是解题目标和方向的直接体现,同时还能帮助学生更清晰的了解试题的背景和一般规律,积累探索解题方向的经验．

5．反思变式探究

每年的高考真题有很多来源于课本和以前的真题,因此,高考真题是教师命题的源泉,为教师命题提供了良好的素材．

根据思路一可得如下变式:

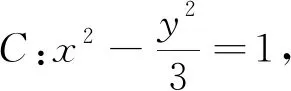
调整设问方式有如下变式:

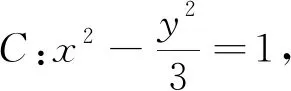
根据思路二和思路三可得如下变式:

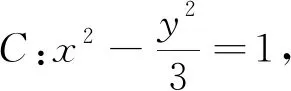
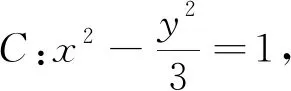
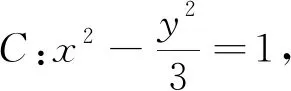
注意到题干中直线AB是经过双曲线C的右焦点F的,那么是否当M是AB的中点时,AB一定过焦点F呢?

通过上述过程可以发现,直线AB不一定过焦点F,因此,我们可以得到如下更一般的变式:

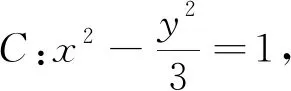
对于任意的双曲线上述命题同样成立,即与双曲线的离心率无关,限于篇幅,不再赘述．

一道优美的试题蕴含着丰富的应用价值,等待着教师和学生深入的探索．通过审读目标条件、探索解题方向、图示解题思路、实施调整运算、反思变式探究五步曲的深入挖掘,可以促进学生数学抽象、直观想象、逻辑推理、数学运算等核心素养的提升,促进素养课堂的达成,助力教师的专业成长．