挖掘图形特征 确定解题路径*——以2022年新高考Ⅰ卷第16题为例

福建省福清第一中学 (350300) 郭海萍

福建省福清市教师进修学校 (350300) 林新建

解析几何问题一直是数学高考的难点,它的“难”在于“运算”,这给学生的解答带来较大的挑战．为此,教学中教师应引领学生学会运用数学抽象的方法,借助直观想象,从问题中的条件,挖掘其几何图形特征,进而选择合理的解题路径,将问题得以简便求解．本文以2022年新高考Ⅰ卷一道试题为例,就如何基于数学抽象,借助直观想象,挖掘图形特征指引解题进行探析,与同仁交流．

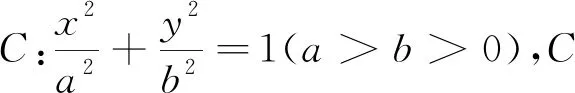
本题以椭圆中求解三角形周长为背景,考查椭圆的标准方程和几何性质,考查数形结合、化归与转化思想,考查数学抽象、直观想象、逻辑推理、数学运算等数学核心素养,体现基础性、综合性、创新性,难度较大．

1 解法探析

本题已知的是椭圆的离心率,及过焦点F1且垂直于AF2的直线DE,待求的是△ADE的周长,由于看不出△ADE的形状,若通过分别求三角形三边长而得,显然计算量较大．为此,需要对题设条件的数量关系作感知,以发掘条件的隐含信息,进而得出图形的关键特征,对所求问题进行转换,有效解决问题．

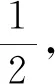
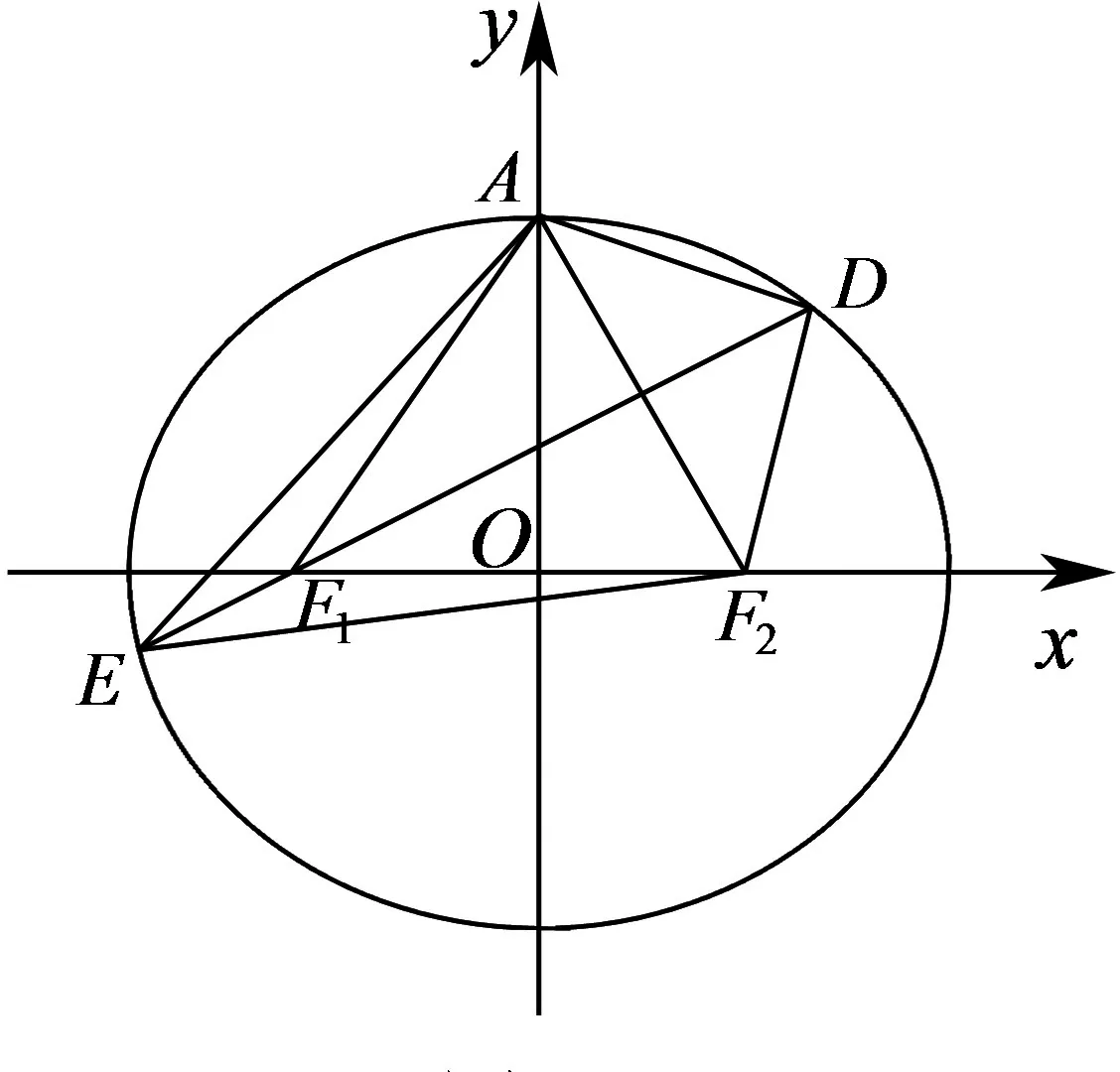
图1

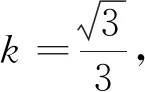
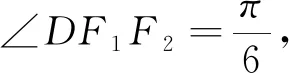
评注：高考命题者试图通过学生对图形特征的挖掘和解题路径的选择来考查和区分学生,此问题可谓以几何特征优化思考,以关键线段确定方向,以长度或角度算法构建要素,是一道体现数学学科价值的好题．

2 策略剖析

本题若分别求出△ADE三边的长,计算量会比较庞大,所以要基于直观想象和数学抽象,从问题中的数量关系,充分挖掘图形的几何特征,建立形与数的联系,进而将△ADE的周长转化为求两个焦点三角形的部分边长和,这是本题的价值所在．同时,对于如何由弦长|DE|=6,求解出c,也是要挖掘图形几何特征,构建数学问题的直观模型,进而选择合理的解题路径,最终将问题求解．

解析几何问题解决的三步曲如图2所示,问题解决关键的一步就是转化的过程,既可以对问题中的数量关系进行感知,挖掘图形的几何特征性质,然后进行代数化;也可以对已有的几何条件进行深挖,得出相关的几何性质,再进行代数化．即“解析几何问题→几何性质→代数问题”．几何特征性质挖掘得越充分,得到的代数化的形式就越简洁,这样,代数运算也就越简捷．

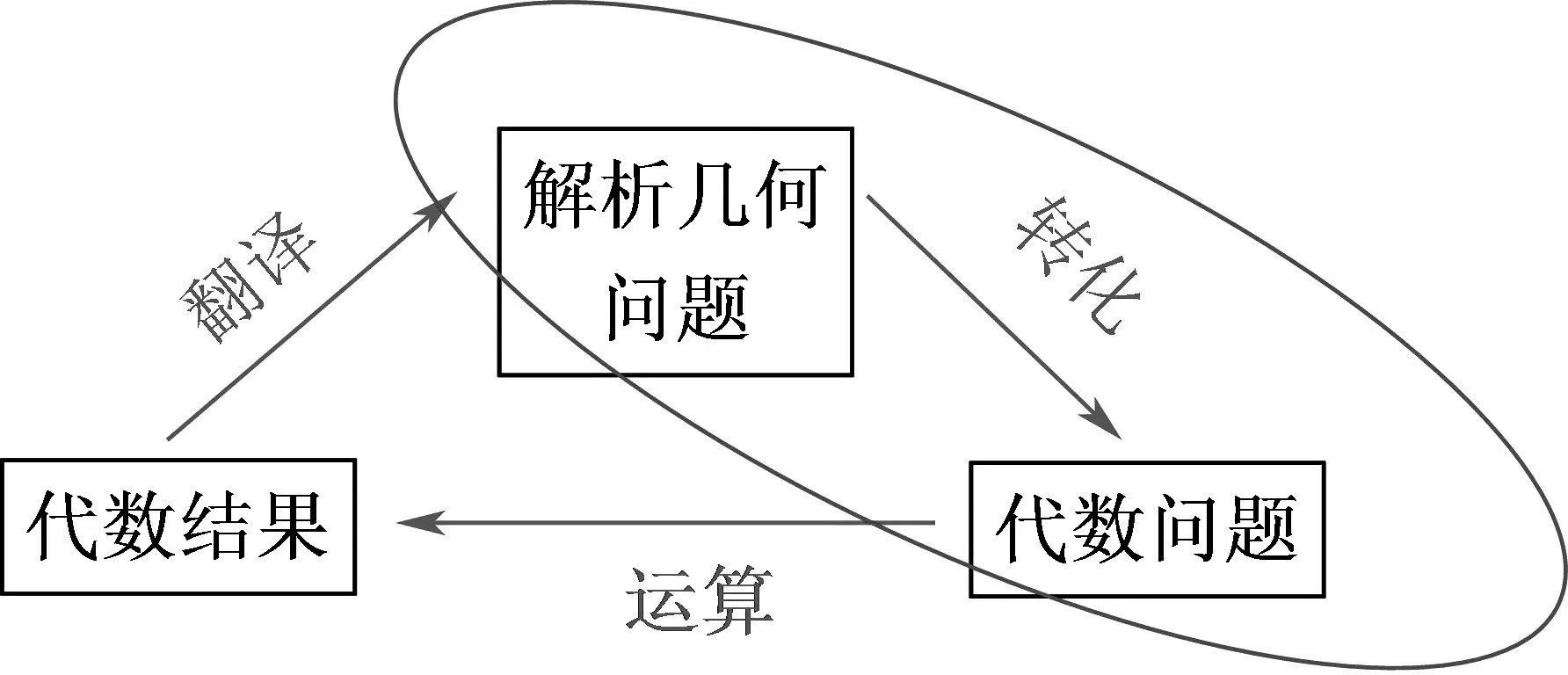
图2

3 应用赏析

在历年高考中,有相当一部分解析几何试题,都可以借助数学抽象的方法,运用直观想象,挖掘其图形特征及性质,进而将问题化归转化,从而有效简化解题过程．

例1(2019年全国Ⅰ卷理科第10题)已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点．若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( ).

解析：基于数学抽象和直观想象,从问题中的数量关系,充分挖掘几何图形特征．如图3,设|BF2|=t,由于|AF2|=2|F2B|,|AB|=|BF1|,所以|AF2|=2t,|BF1|=3t,由椭圆定义得|AF1|+|AF2|=|BF1|+|BF2|=2a,可得|AF1|=2t,从而|AF1|=|AF2|,由此得点A为椭圆的上顶点或下顶点,则△AF1F2为等腰三角形．

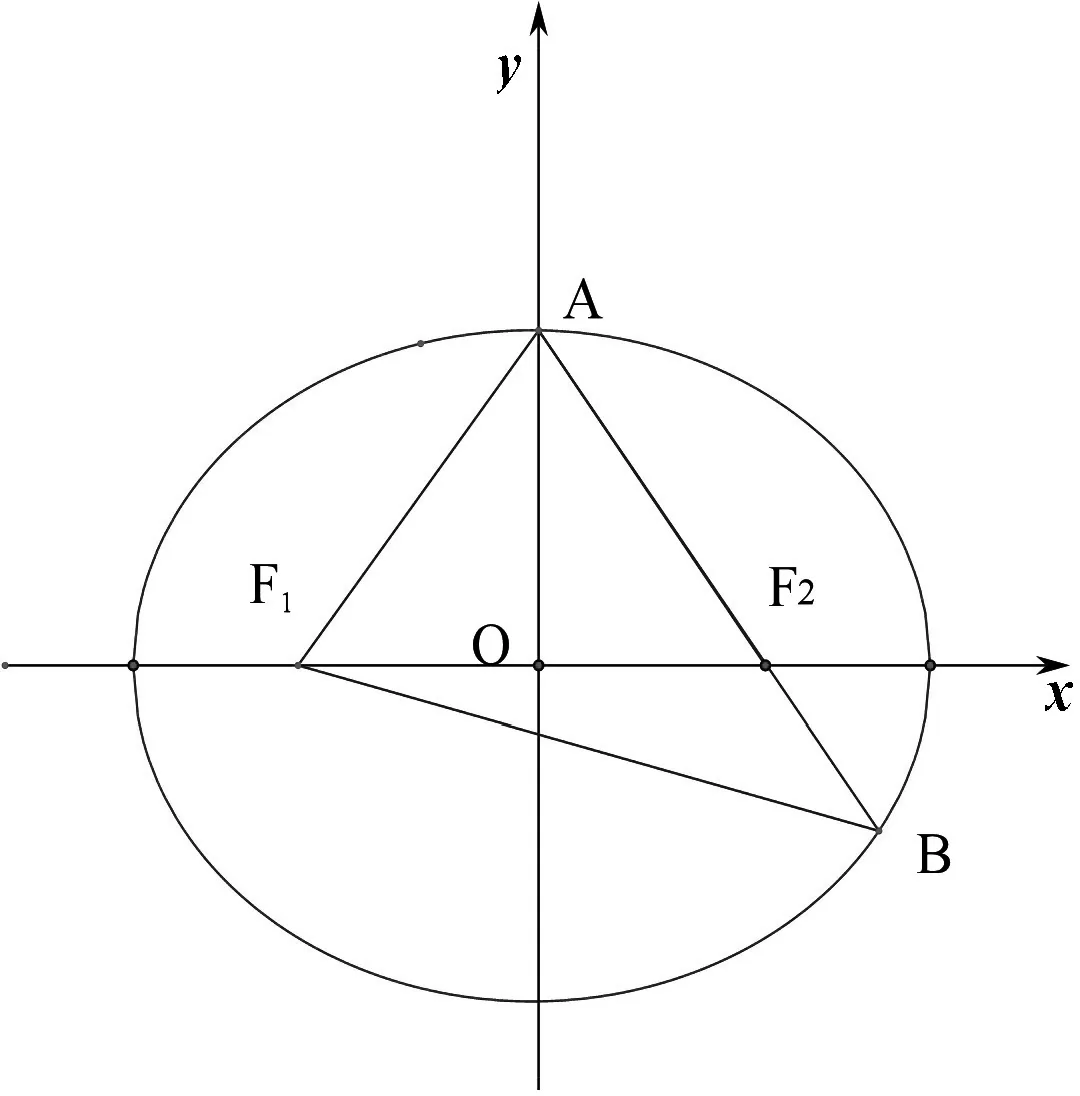
图3

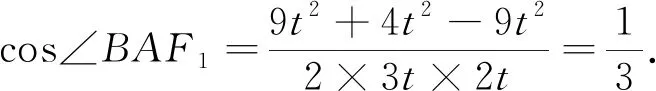
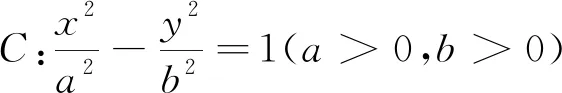
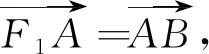
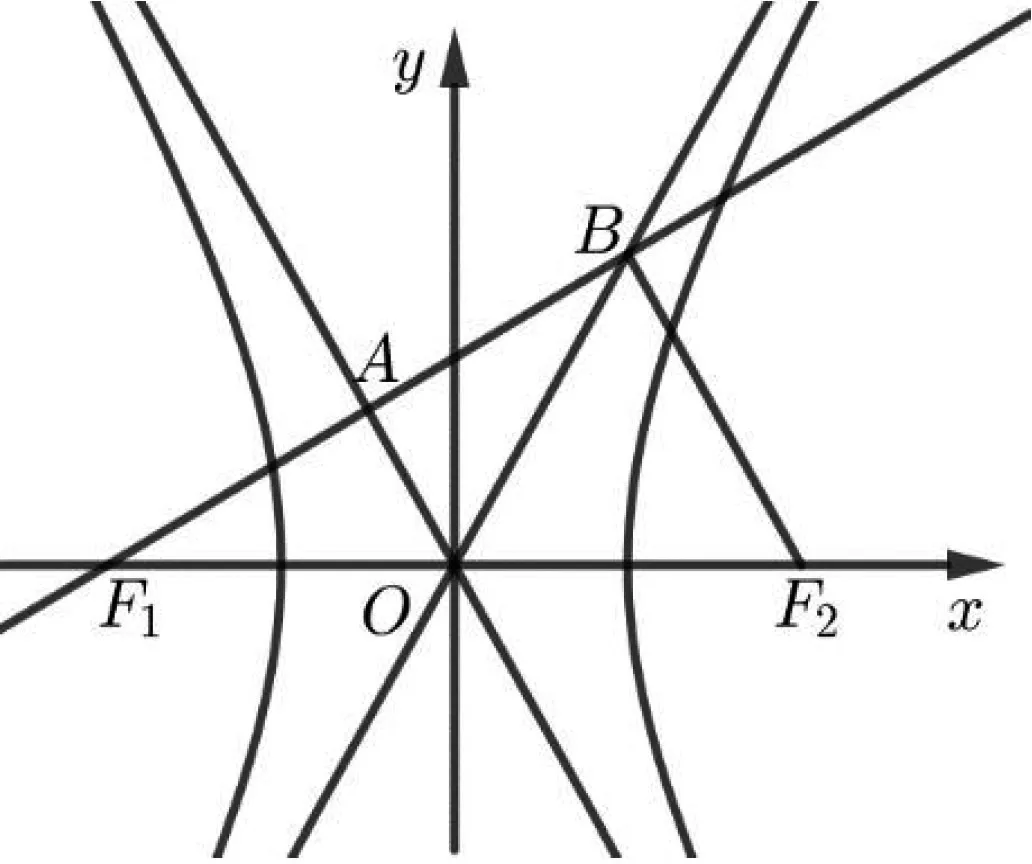
图4

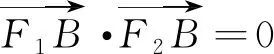
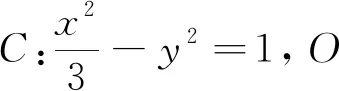
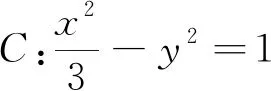
若通过设直线MN方程,与渐近线方程联立,分别求出点M、N的坐标,进而用两点距离公式求出MN的长,思路直观,但运算量偏大,费时费力．若运用直观想象,挖掘其图形特征,将问题转化,快捷求解．

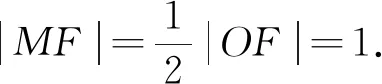
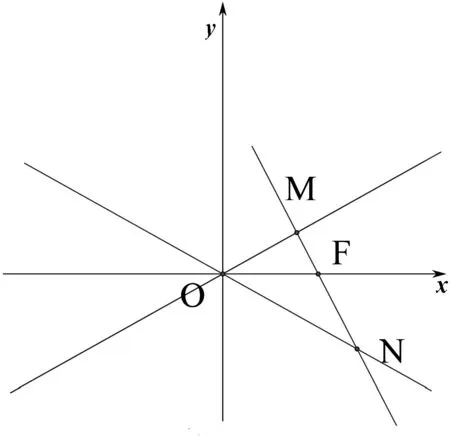
图5

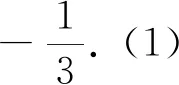
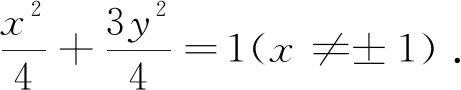
(2)假设存在满足条件的点P(x0,y0),如图6,由△PAB与△PMN的面积相等可得|PA|·|PB|

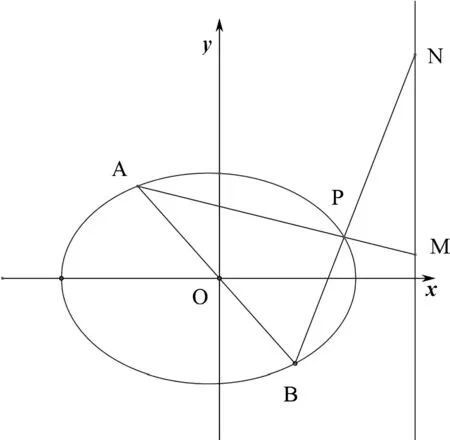
图6

=|PM|·|PN|,但由于M、N的坐标未知且不易求得,许多考生至此望而却步．

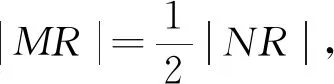
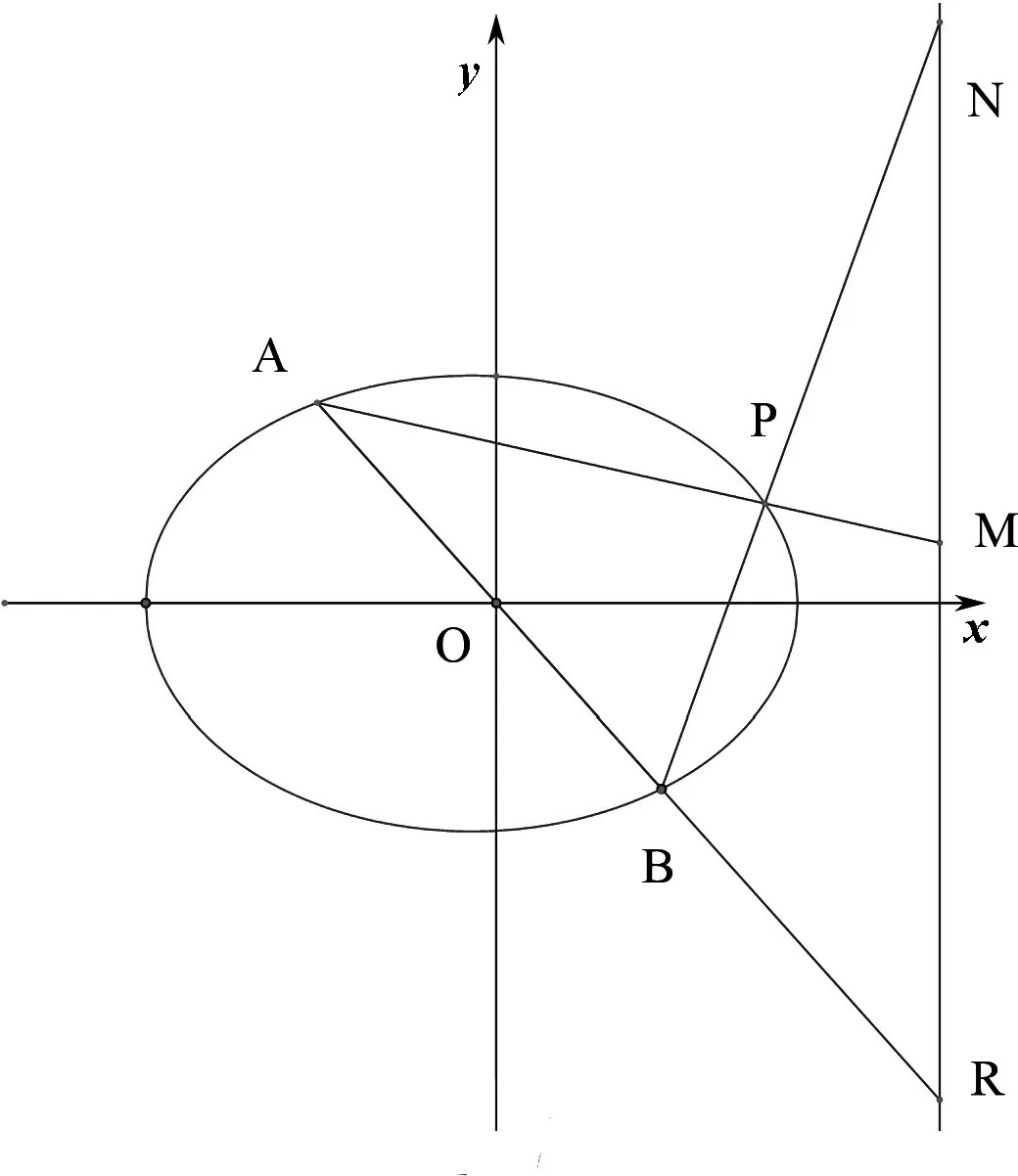
图7

4 素养综析

对于解析几何问题,它的特点是“运算”,而它的难点也是在运算上,而能力恰恰体现在“如何简化运算”上．简化运算,这不仅与巧设点坐标与直线方程有关,还与运算路径的选择有关,更与问题中的图形特征和几何性质的挖掘有关．所以,在教学过程中,教师要引导学生会用数学眼光去观察问题,即数学抽象,从数量关系中去挖掘图形的几何特征,巧妙转化,培养数学抽象和直观想象素养;同时还要引导学生会用数学思维去思考问题,即逻辑推理,由图形特征确定合理的解题路径,合理引入参数,进行多元表征,将几何条件代数化,求得正确的运算结果,培养逻辑推理和数学运算素养．