圆锥曲线问题中求定直线方程的若干思路

福建省福安市第一中学 (355000) 徐志刚

在一些关于圆锥曲线的综合题中会伴随着探求相关的定直线问题,由于题设条件的不同,其解题方法也是多种多样、精彩纷呈,其中抓住问题特点、挖掘隐含条件、紧盯解题目标是所有解题方法的思维核心.本文通过对近几年的高考模拟题的解题探究和分析,归纳出下面三种常用的思考路径,供读者朋友们参考.

1、求动点坐标找出直线在一些问题中需要证明某个动点在定直线上,我们可以设法用一个参数将此点表示出来,再通过研究找出此动点的变化规律,判定其在一个定直线上.

例1 平面直角坐标系xOy中,已知抛物线y2=2px(p>0)及点M(2,0),动直线l过点M交抛物线于A,B两点,当l垂直于x轴时,AB=4．(1)求p的值;(2)若l与x轴不垂直,设线段AB中点为C,直线l1经过点C且垂直于y轴,直线l2经过点M且垂直于直线l,记l1,l2相交于点P,求证:点P在定直线上．

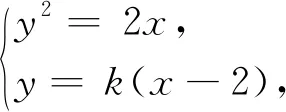
点评：根据已知条件,动点P是两直线l1,l2的交点,这是本题的重要特征,所以问题就转化为如何求得含参数k的直线l1和l2的方程,于是问题的解决比较容易了.

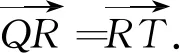
解析：(1)容易得到抛物线C的方程为x2=4y.

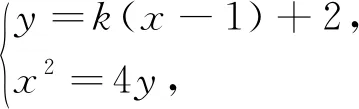
点评：此类问题的特点是,经过常规的推理和运算,可以用一个参数表示出所求的动点坐标,然后根据此坐标通过匹配和变形,求出动点所在的直线方程.

2、联立方程推出直线根据交轨法的思路,将动点看成是两直线(曲线)的交点,然后对两直线方程进行整体变形和运算,经过消元转化可直接得到定直线的方程.

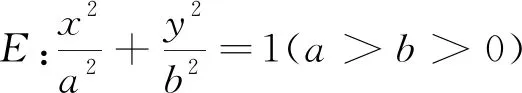
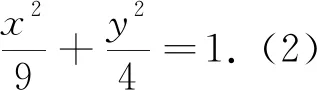
点评：本题中的几何条件比较多,如点B、C都在椭圆上,两点关于y轴对称等等,抓住这些可进行简化设点,也降低了消元难度,压缩了解题过程,减轻了解题的麻烦．

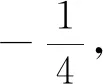
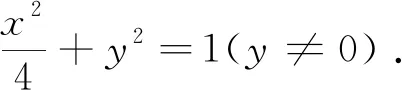
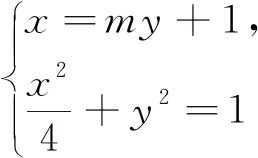
点评：在将两个方程联立后,如何化简、如何消参就显得非常重要了,此时必须关注所设的相关参数的意义,联想到直线与圆锥曲线相交的特点和特定变换模式,提供整体变形转化可解决问题.

3、转化思考挖出定直线在深刻理解题意的基础上,抓住题中的某一些关键条件,换一个方向重新解释题意,打开新的思路,这样就能获得破题机会.

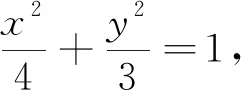
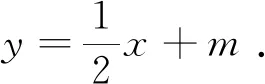
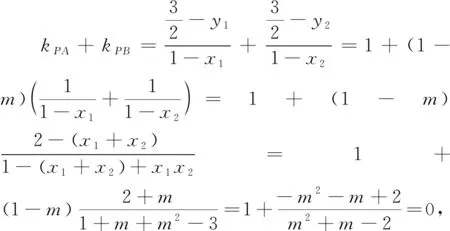
点评：由于题中所需确定的三角形的圆心在某定直线上,直接思考是比较困难的,但换一个思路,内切圆与三角形的内角平分线相关,并且定直线x=1与y轴垂直,故而可从寻找直线PA,PB的斜率关系人手.

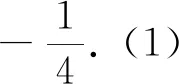
点评：运用待定系数法是解决相关参数的重要的方法,本题中利用条件建立了一个关于半径r的恒成立的式子,抓住存在定直线的实质,通过比较系数求出参数值,此法是解决定直线系数问题的重要方法.