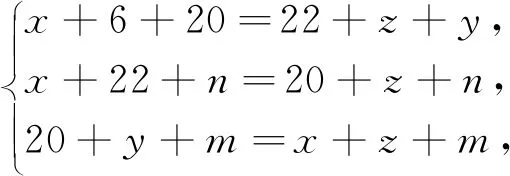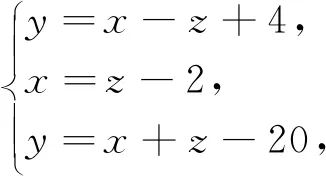分类解析中考试题中的创新题型
2023-05-10湖北省襄阳市第一中学441000杜晓霞
湖北省襄阳市第一中学 (441000) 杜晓霞 王 勇
《教育部关于加强初中学业水平考试命题工作的意见》要求考生对“新颖的信息、情境和设问,选择有效的方法和手段收集信息,综合与灵活地应用所学的数学知识、思想和方法,进行独立思考、探索和探究,提出解决问题的思路,创造性地解决问题.”随着新一轮课程改革的深入和推进,中考的改革使知识立意转向能力立意和素养立意,强化学科素养和关键能力的考查,推出了一批新颖而又别致,具有创新意识和创新思维的新题. 本文采撷中考题中的创新题型并予以分类解析,旨在探究题型规律,揭示解题方法.
1 定义新的概念
例1 (2022·上海市中考题)定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为2的等腰直角三角形,当等弦圆最大时,这个圆的半径为________.
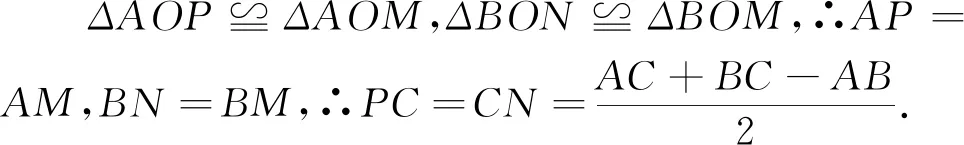
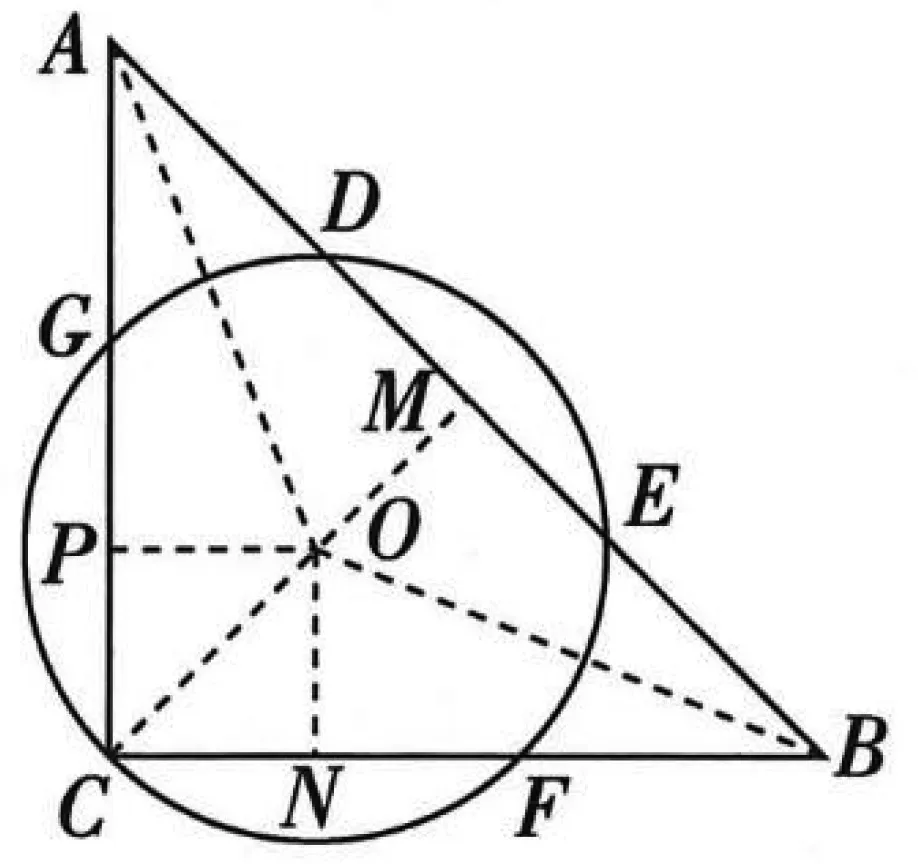
图1
点评:本题在理解“等弦圆”实质的基础上结合平面几何知识即可顺利解决问题.
2 约定新的运算
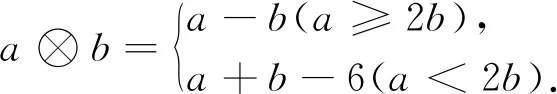
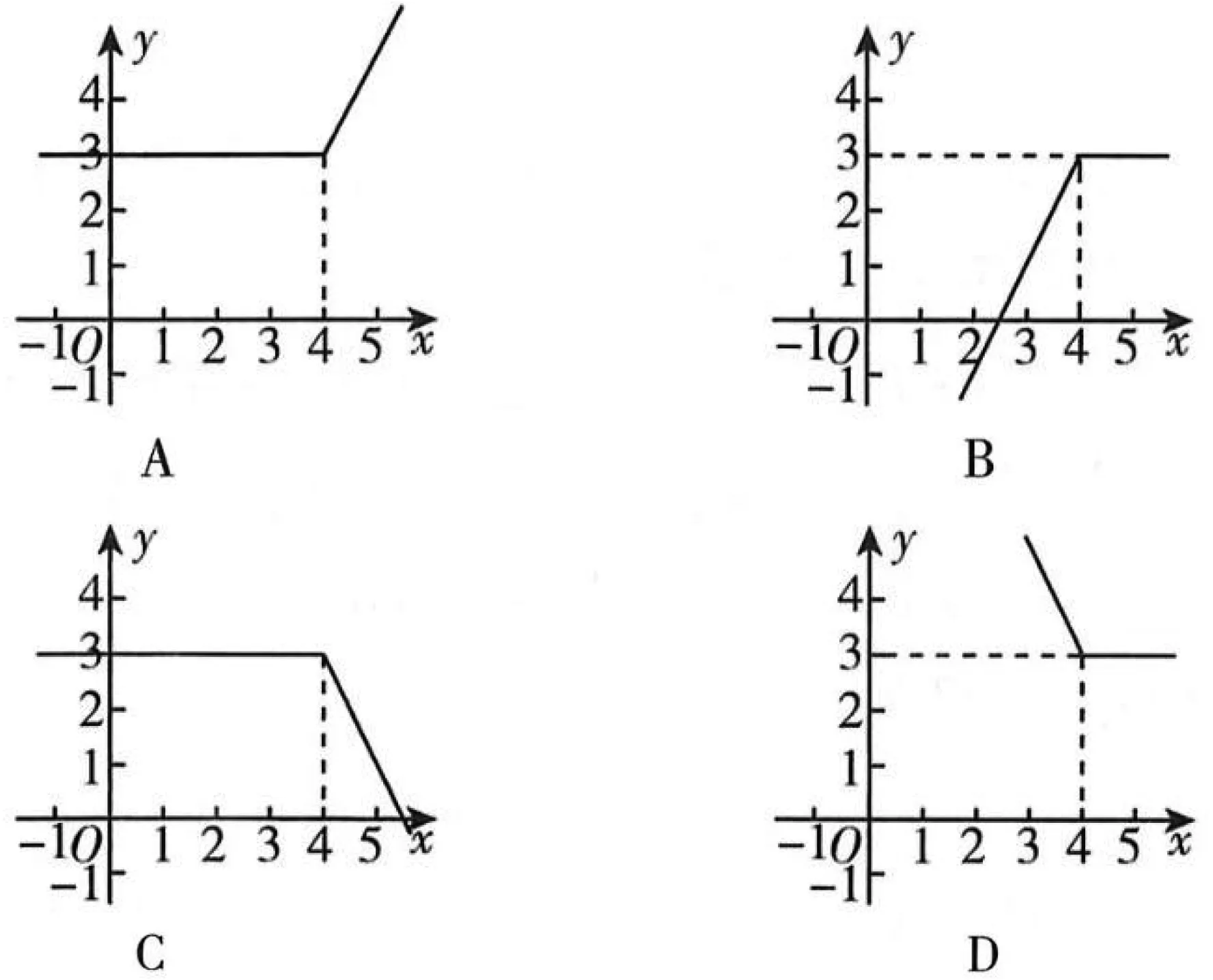
解析:当x+2≥2(x-1),即x≤4时,y=(x+2)⊗(x-1)=x+2-(x-1)=3;当x+2<2(x-1),即x>4时,y=(x+2)⊗(x-1)=x+2+x-1-6=2x-5. 综上所述,选项A中的图象符合题意,故选A.
点评:本题由约定的新运算可知所给函数是一个分段函数,具体求出解析式并结合选择支即可快速获解.
3 引入新的记号
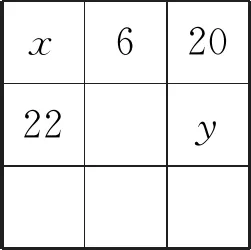
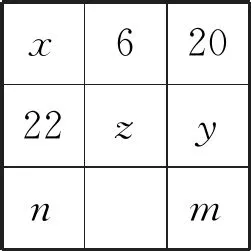
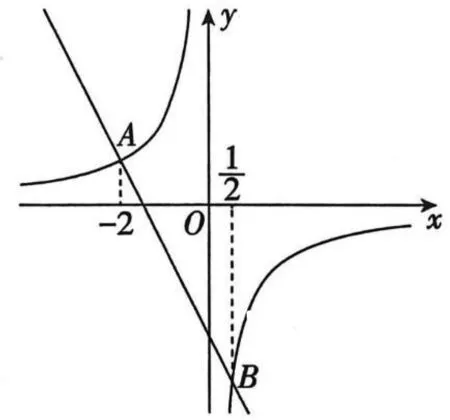
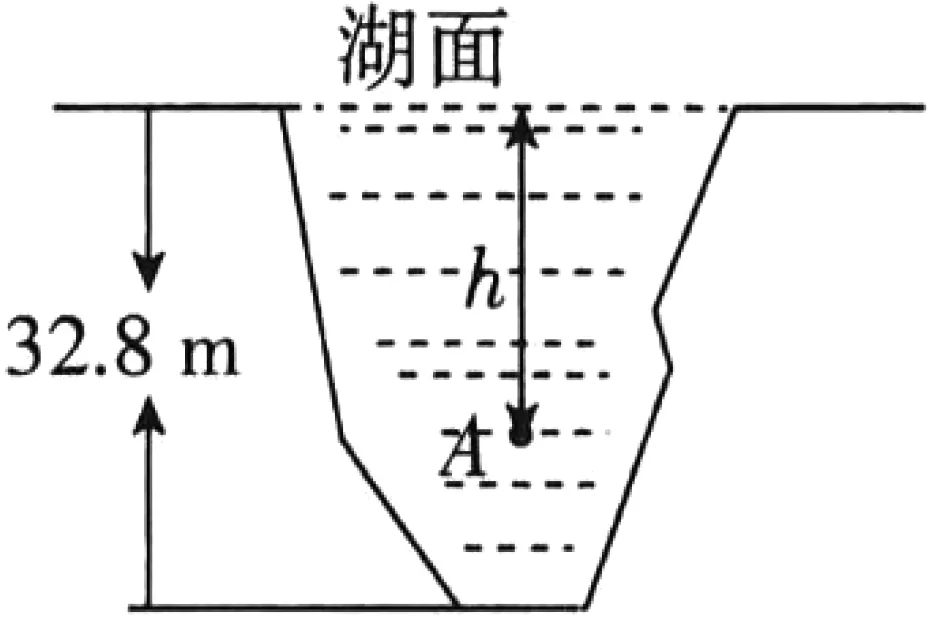
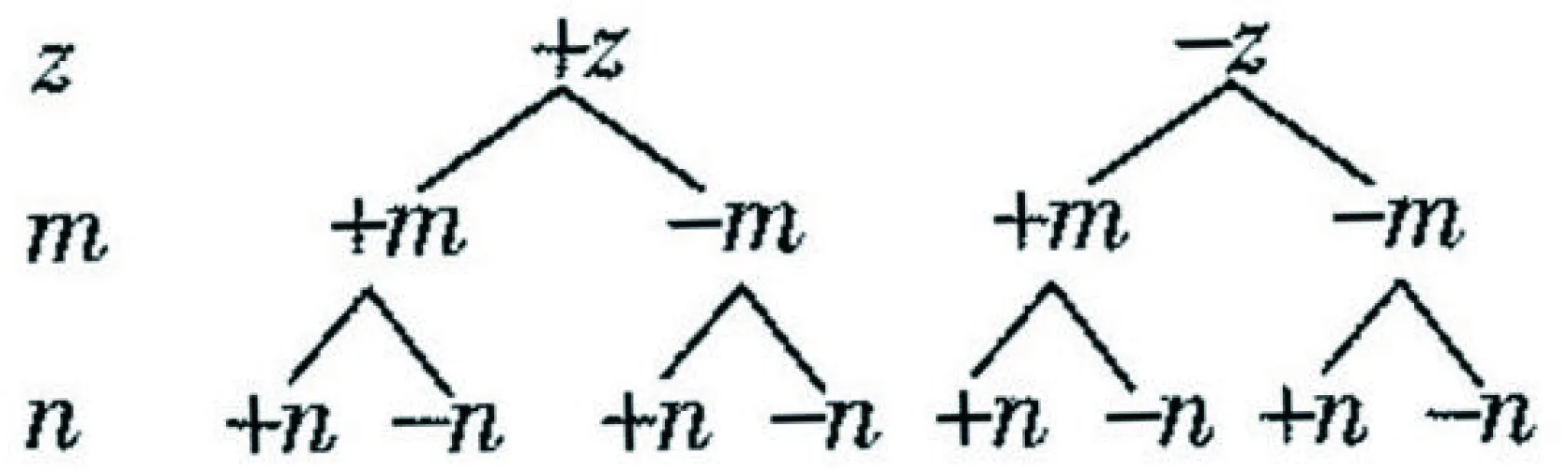
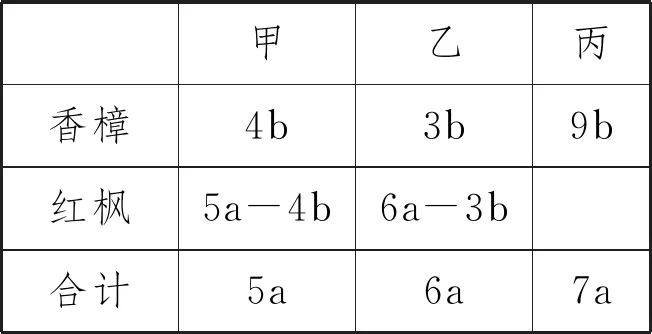
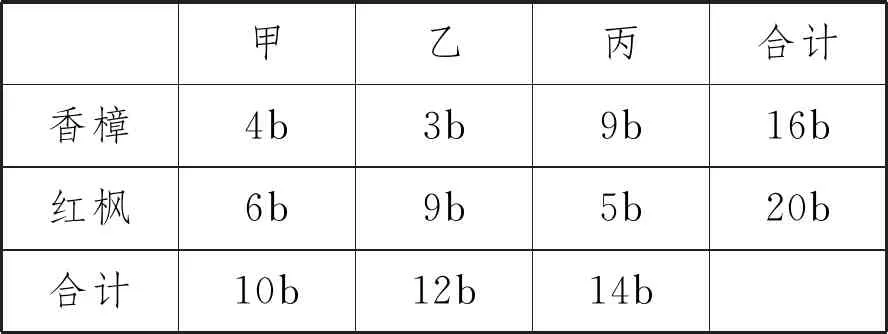
例3 (2022·赤峰市中考题)阅读下列材料:引入记号:min{a,b},当a≥b时,min{a,b}=b;当a 图2 解析:(1)易得(1)为①1,②-4. 点评:本题是“最值函数”记号,弄懂min{a,b}的实质内涵是解决第(1)问的关键,再结合数形结合思想和待定系数法即可轻松解决第(2)问. 例4 (2022·恩施州中考题)图3(1)是我国青海湖最深处某一截面图,青海湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=kh+P0,其图象如图3(2)所示,其中P0为青海湖水面大气压强,k为常数且k≠0.根据图中信息分析(结果保留一位小数),下列结论正确的是( ). 青海湖最深处某一截面图 A. 青海湖水深16.4m处的压强为188.6 cmHg B. 青海湖水面大气压强为76.0 cmHg C. 函数解析式P=kh+P0中自变量h取值范围是h≥0 D.P与h的函数解析式为P=9.8×105h+76 点评:本题是数学与物理的跨科综合题,考查数形结合思想、待定系数法,考查考生的运算求解能力. 例5(2022·重庆市中考题)在多项式x-y-z-m-n中任意加括号,加括号后仍只有减法运算,然后按给出的运算顺序重新运算,称此为“加算操作”. 例如:(x-y)-(z-m-n)=x-y-z+m+n,x-y-(z-m)-n=x-y-z+m-n,…. 下列说法:①至少存在一种“加算操作”,使其运算结果与原多项式相等;②不存在任何“加算操作”,使其运算结果与原多项式之和为0;③所有可能的“加算操作”共有8种不同的结果.其中正确的个数为( ). A. 0 B. 1 C. 2 D. 3 解析:当添加一个括号,且左括号在x前边时,右括号在任何一个位置,运算结果都与原多项式相等,故说法①正确. 由于不管在哪个位置添加括号都无法改变前两项的符号,因此运算结果与原多项式之和不可能为0,故说法②正确. 根据“加算操作”的原则,不会改变前两项的符号,改变的是后三项的符号,画示意图如图4所示,据图可知共有8种不同的结果,故说法③正确.故选D 图4 点评:本题给出的情境新颖别致,考查考生的阅读理解能力和逻辑推理能力. 例6(2022·重庆市中考题)为进一步改善生态环境,村委会决定在甲、乙、丙三座山上种植香樟和红枫.初步预算,这三座山各需两种树木数量和之比为5:6:7,需香樟数量之比为4:3:9,并且甲、乙两山需红枫数量之比为2:3.在实际购买时,香樟的价格比预算低20%,红枫的价格比预算高25%,香樟购买数量减少了6.25%,结果发现所花费用恰好与预算费用相等,则实际购买香樟的总费用与实际购买红枫的总费用之比为_________. 表(1) 表(2) 点评:本题是列方程解应用题,由于数量关系错综复杂,导致众多考生无法正确求解.本题采用设未知数并充分利用表格法方可顺利求解,此方法值得同学们细细品味和充分借鉴. 点评:本题以我国数学家秦九韶的“三斜求积术”为载体,考查考生的阅读理解能力和运算求解能力.弘扬和传承魅力无穷的数学文化,激发学生学习数学的乐趣和内在动力. 例8 (2022·武汉市中考题)幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图5 就是一个幻方.图6是一个未完成的幻方,则x与y的和是( ). 图5 图6 A.9 B.10 C.11 D.12 解析:设最中间、第三行最左侧、第三行最右侧的数分别为z,n,m,如图7所示,根据题意可得 图7 点评:本题以“幻方”为背景考查代数推理,合理设出未知数,紧扣“每一横行、每一竖列以及两条对角线上的3个数之和相等”列出方程组求解即可.考查考生的逻辑思维能力和运算求解能力.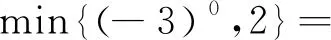
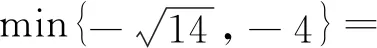
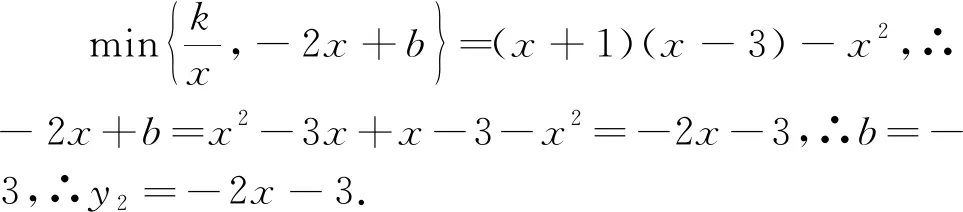
4 设置新的交汇
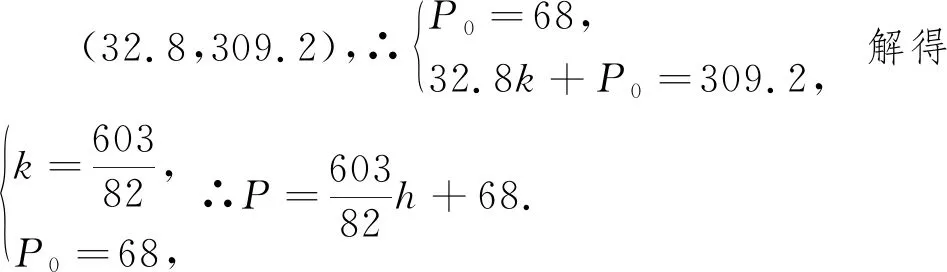
5 创设新的情境
6 建模新的应用
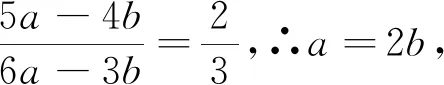
7 渗透数学文化