例析整体代换在一道三角函数问题中的运用

上海中学东校 (201306) 汪海鹏

三角函数图像性质问题一直是高考数学试题中的常考问题,在破解此类问题时,经常用到“整体代换”的思想方法.整体代换方法可以实现化繁为简、简便运算,对一些难度较高的三角函数问题可以达到事半功倍的效果.本文结合实例探析“整体代换”在三角函数问题中的应用.

1.问题呈现

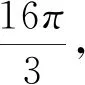
此题以三角方程为背景,题目简单清晰,看似是三角方程求解的内容,实质上融合了三角函数图像性质以及图像变换的知识.在具体的破解过程中,可以借助解三角方程、数形结合、分类讨论、整体代换等不同的思维来综合处理,从而有效切入,准确破解.

2.问题破解

(1)解三角方程思维

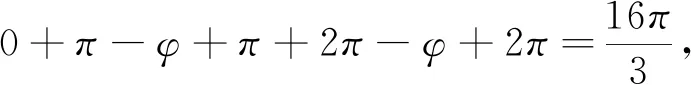
点评：利用条件对方程中的参数a进行分析代换,解三角方程得到通解,并结合φ的取值范围进行分情况讨论,进而解出不同范围内符合条件的φ值.

(2)三角函数思维

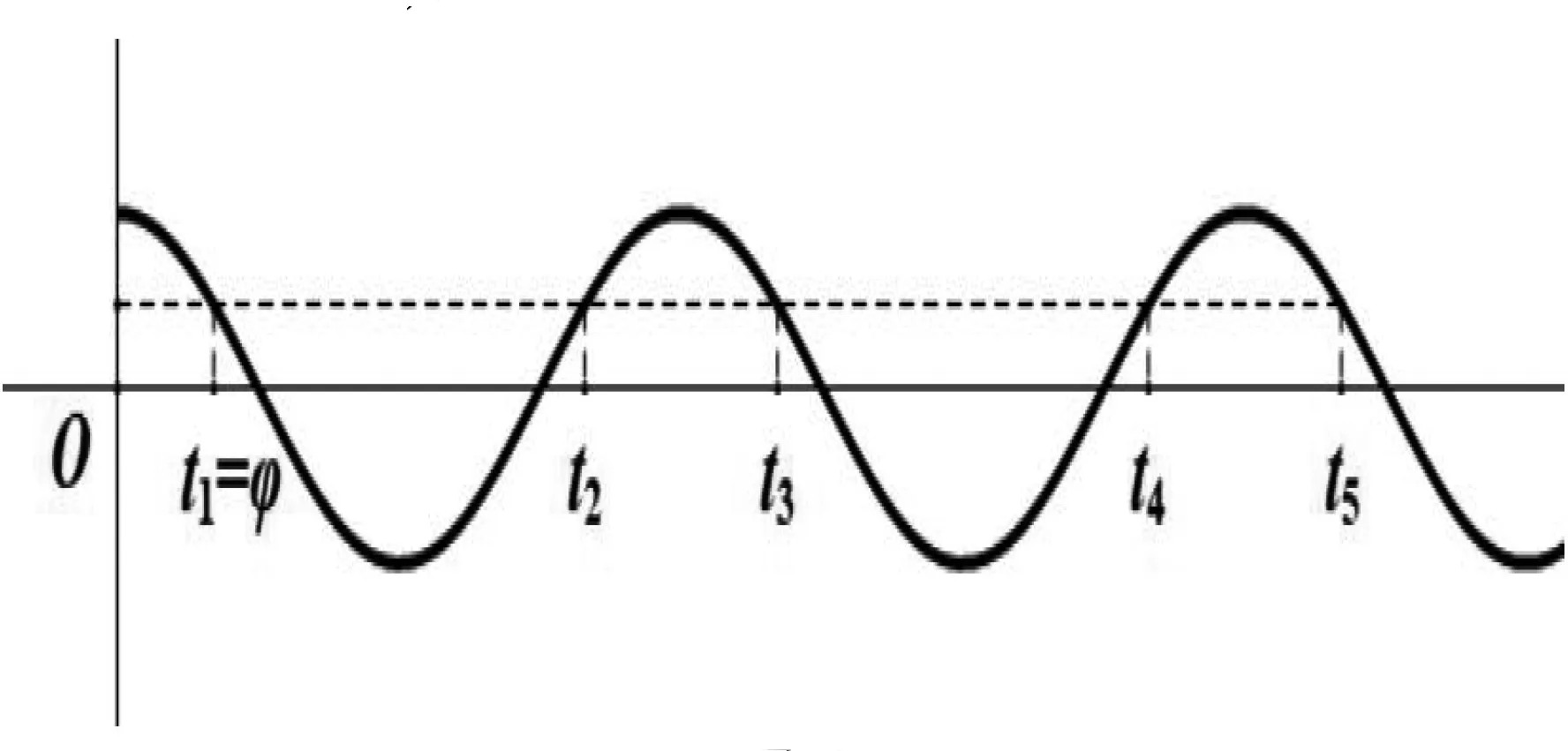
图1

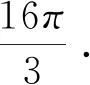
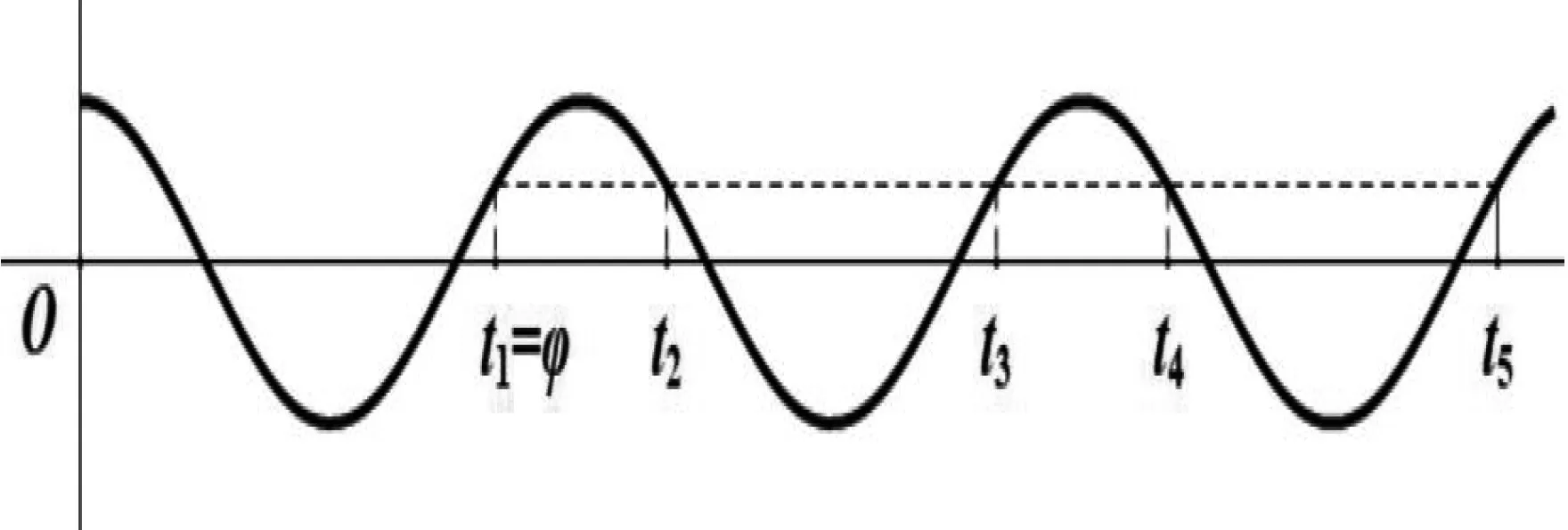
图2

点评：借助整体代换思维将原问题转化为余弦曲线上的问题,便于画草图进行数形结合,再结合函数图像的对称性质,对参数加以分类讨论,通过参数值的方程破解问题.

3.链接高考

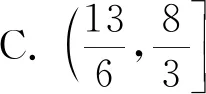
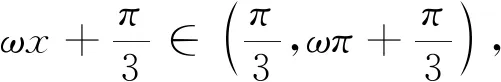
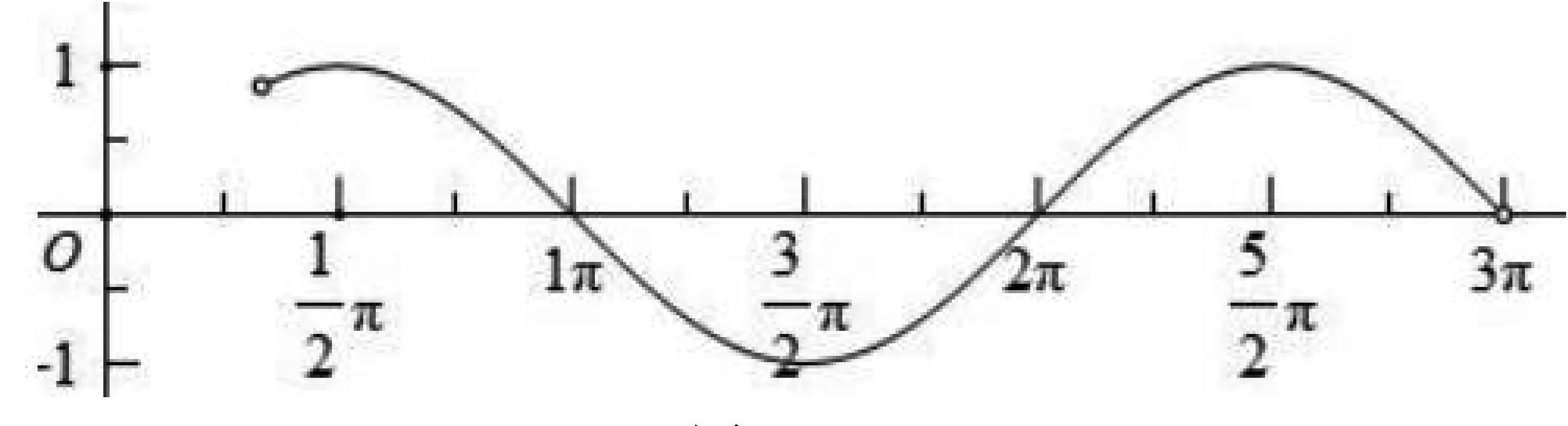
图3

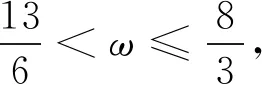
巧妙借助整体代换的思想,将问题转化到余弦曲线上,从而大大降低了作图难度,便于数形结合,得以正确求解.这种类型题目一般难度较大,重点考查学生应用所学知识分析和解决问题的能力.“整体代换”是解决三角函数图像性质问题的常用代数方法,通常再搭配数形结合的思想不仅可以使问题变得简单明了、容易下手,而且在解决问题的过程中减少了不必要的细节分析和画图的麻烦.