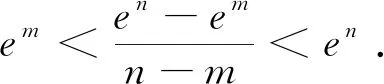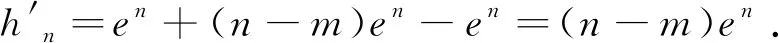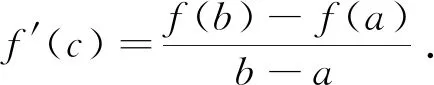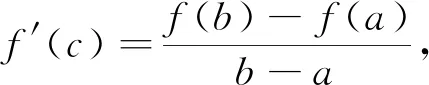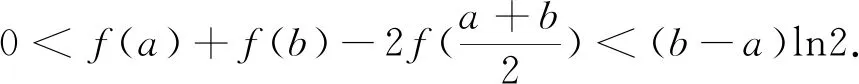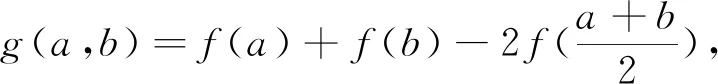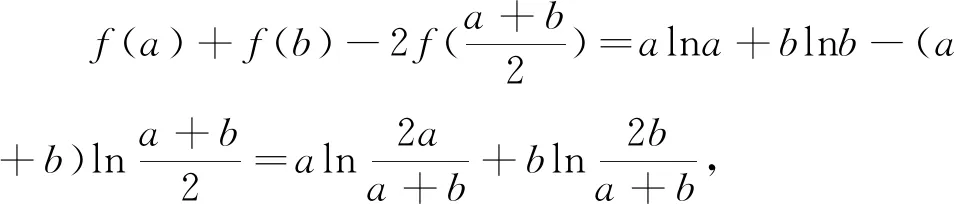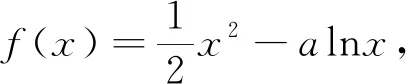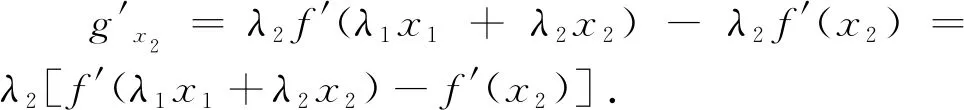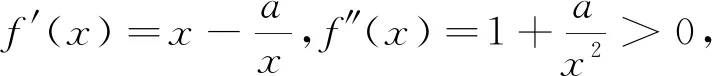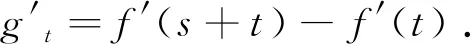用固定变量,分步递进法解决一类双变量函数问题

陕西省汉中市龙岗学校 (723103) 唐宜钟

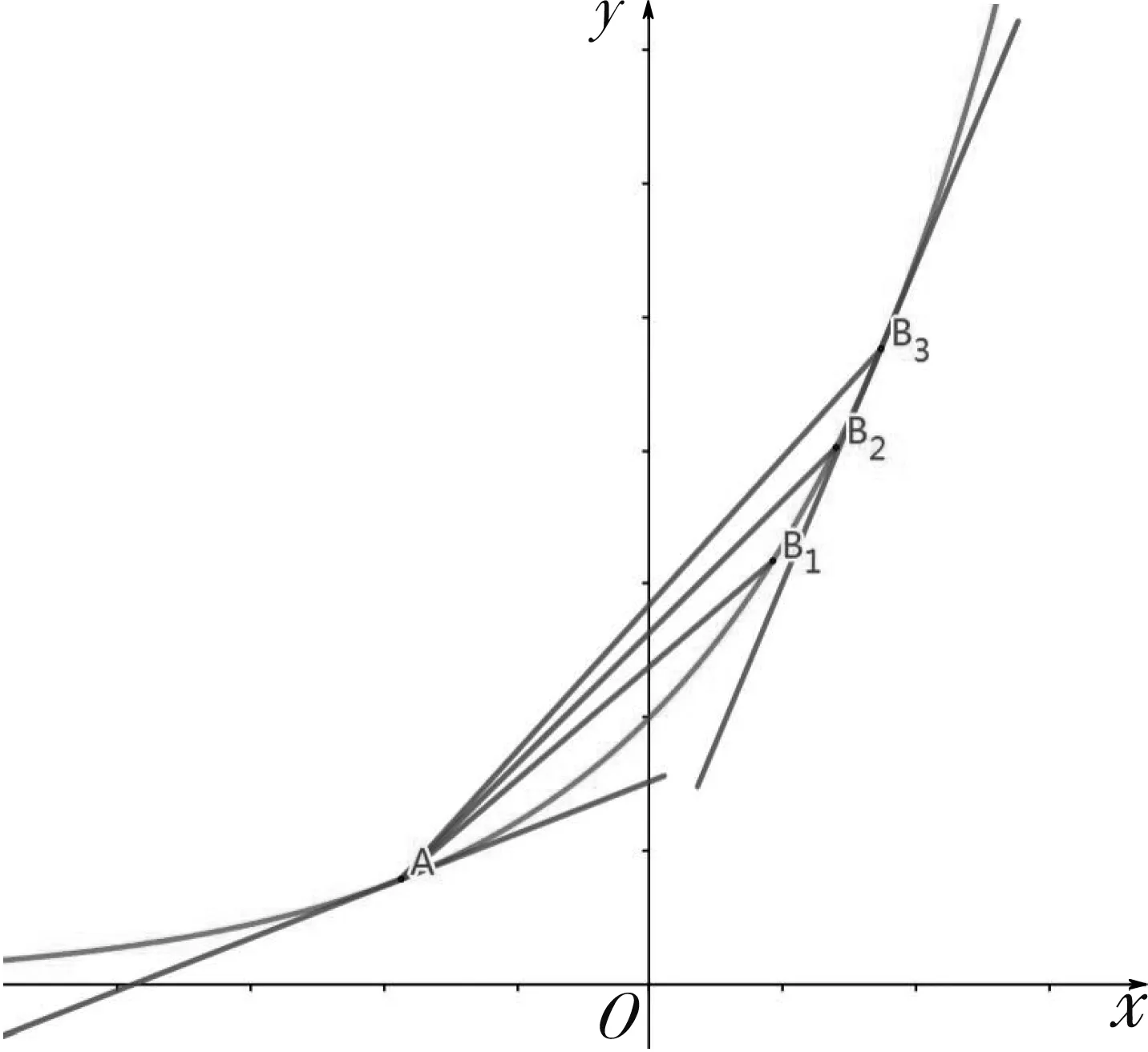
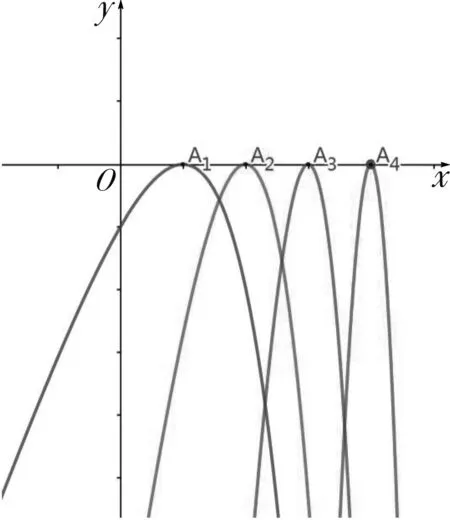
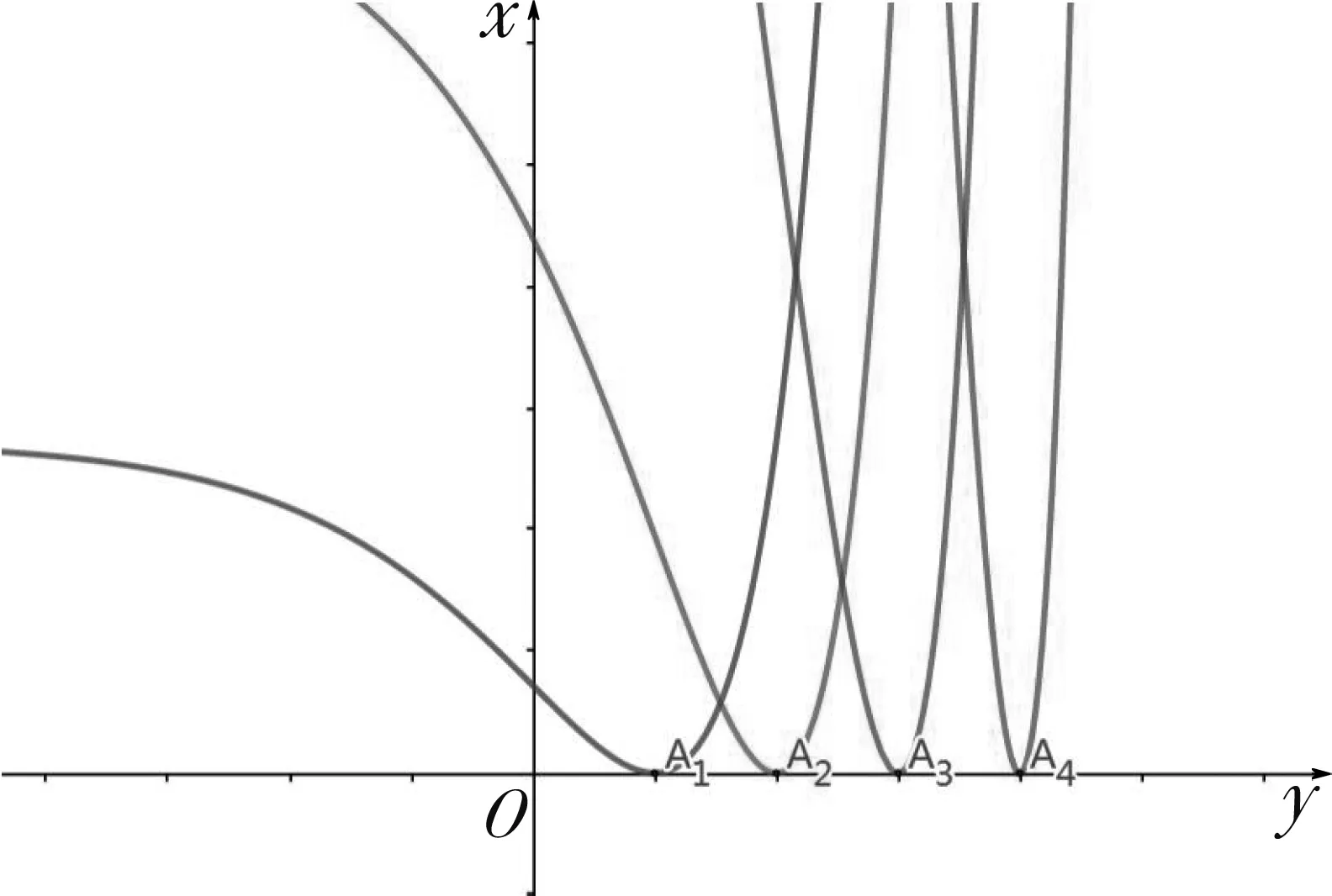
近年来,一类双变量函数问题在高考、模拟题中频频出现.这类问题可大致表述为:已知双变量函数y=f(s,t),其中s,t∈(m,n),证明:A

例1 已知函数f(x)=ex,A(m,em),B(n,em)(m

评注：本题可做如下理解.固定m,即点A固定.如图1,B离A越远,kAB越大.当B→A时,kAB越来越小,直至A,B重合时,kmin=f′(m).同理,固定n,即点B固定.当A→B时,kAB越来越大,直至A,B重合时,kmax=f′(n).

图1

对于函数g(m,n),mh(m,m).

图2

图3

评注：本题的背景是“琴生”不等式.在固定x1后,函数的单调性依旧无法得出,需借助二阶导,有一定的思维度.但当写出f′(λ1x1+λ2x2)-f′(x2),求二阶导就水到渠成.

例5 已知函数f(x)=exln(1+x)．证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).

评注：通过前面例证不难发现,对于大多数双变量函数y=f(s,t),其最值取等条件为s=t,而f(s,s)=0.但对本题而言,g(s,s)的值并不确定,还需计算φ(s)=g(s,s)的最小值.其转化路径为(s,t)→(s,s)→(0,0).

通过以上例证,不难感受到采用固定变量,分步递进的方式处理一类双变量函数问题流程固定,思维顺畅,计算简洁,几乎用不到任何变形技巧.但这类问题要求双变量在给定范围类可以自由取值,双变量之间没有等量代换关系.在实际做题过程中,需仔细辨别,不可盲目套用.