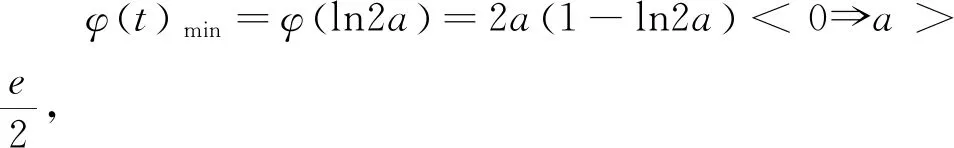巧用同构,破解函数方程、不等式综合问题*
2023-05-10湖南省长沙市周南中学410008易长保
湖南省长沙市周南中学 (410008) 易长保
湖南省长沙市第一中学 (410005) 张自力
数学中的同构,就是通过等价变形,将方程或不等式左右两边变成结构相同的式子,根据问题需要,找到与之紧密关联的特殊函数,再将关联的函数的基本性质迁移并运用于问题解决的过程,其“化繁为简”的效果受到广大命题者的喜爱,本文将从同构基础、同构应用、同构迁移三个方面进行阐述,力求达到巧用同构,破解函数方程、不等式等综合问题.
一、同构基础
我们在学习指对数运算性质时,曾经提到过两个这样的恒等式:
当a>0且a≠1时,有alogax=x(x>0),logaax=x.再结合指对数运算的性质,可以得到如下结论(x>0):
类型一:(和结构) 函数y=ex±x与y=x±lnx关联同构;这是因为y=ex±x=ex±lnex,y=x±lnx=elnx±lnx.
类型二:(积结构) 函数y=xex与y=xlnx关联同构;这是因为y=xex=exlnex,y=xlnx=(lnx)elnx.
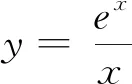
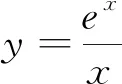
二、同构应用
问题一 利用同构解决不等关系
例1 (2020·新课标I卷理12)若2a+log2a=4b+2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 分析:本题呈现的是一个等式,右边适当变形得4b+2log4b=22b+log22b-1,进而根据两边特征同构,找到与之关联的函数,借助函数的单调性即可解决问题. 解析:因为2a+log2a=4b+2log4b,而4b+2log4b=22b+2log22b=22b+log2(2b)-1,所以2a+log2a=22b+log2(2b)-1<22b+log2(2b),观察结构特点,很容易找到对应的关联函数f(x)=2x+log2x(x>0),则f(a) 问题二 利用同构求函数最值 例2 已知f(x)=xex,g(x)=xlnx,若f(m)=g(n)=t(t>0),则mn·lnt的取值范围为( ). 分析:妙用指对关系,由mem=nlnn=elnn·lnn,找到同构函数f(x),借助f(x)的单调性得到m,n间关系,再借助g(x)单调性求得最值. 问题三 利用同构解决函数的零点或不等式恒成立问题问题 例3 已知函数f(x)=aex-ln(x+2)+lna-2,a∈R.(1)若f(x)仅有两个零点,求实数a的取值范围;(2)若f(x)>0恒成立,求实数a的取值范围; 分析:(1)由函数零点的定义,将方程进行变形,转化为ex+lna+x+lna=ln(x+2)+eln(x+2),找到同构函数h(x)=ex+x,由h(x)的单调性,将问题转化为lna=ln(x+2)-x,再构造函数φ(x)=ln(x+2)-x,x>-2,利用导数研究其单调性和φ(x)的最值问题,即可得到实数a的取值范围. (2)由(1),将问题转化为lna>ln(x+2)-x恒成立,构造函数φ(x)=ln(x+2)-x,x>-2,借助φ(x)最值,即可得到实数a的取值范围. (2)由(1)将问题转化为lna>ln(x+2)-x恒成立,求得φ(x)最大值为φ(-1)=1,故lna>1,得a>e,故实数a的取值范围为(e,+∞). 问题四 利用同构证明不等式 例4 (2021全国高考22题)已知函数f(x)=x(1-lnx). (1)讨论f(x)的单调性; 解析:(1)易求得f(x)在区间(0,1]上为增函数,在区间[1,+∞)上为减函数. 令f(x)=x(1-lnx),则有f(m)=f(n),不妨设m 要证m+n>2⟺n>2-m⟺f(n) 再证m+n 例5 已知函数f(x)=xex-2a(lnx+x)有两个零点,求a的最小整数值. 分析:f(x)=ex+lnx-2a(lnx+x),令t=x+lnx,则只需证明φ(t)=et-2at在R上有两个零点,根据函数的单调性求得最值,求得f(x)有两个零点的必要条件,最后通过切线放缩取值,验证充分条件,从而解决问题. 若a≤0,则φ'(t)>0,函数φ(t)在R上单调递增,至多只有1个零点,不合题意; 以上可以看出,对于函数方程、不等式综合问题,我们可以根据式子的特征,适当等价变形,巧用同构的方法来求解,可以避免复杂的导数运算和导函数符号的分类讨论,化繁为简,快速解决问题.
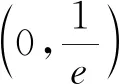
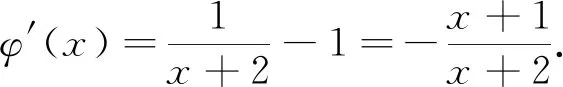

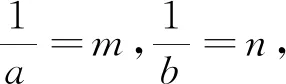
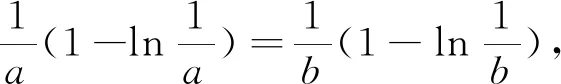
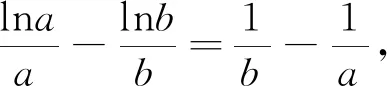
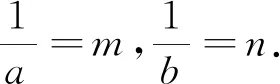
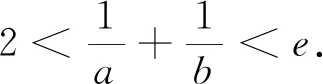
三、同构迁移