一道圆系方程的变式探究

广东省佛山市顺德区罗定邦中学 (528300) 陈 玲

在解析几何问题中,我们接触到的轨迹方程常常都是关于点的轨迹.当某种曲线(以圆为例)按照某种规律进行变化时,也可形成相应的轨迹(本文称其为“圆系”).那么这样的“圆系”会满足什么规律呢?

“圆系”方程,顾名思义即是满足某类条件的一系列的“圆”的方程.常见的构造“圆系”方程的技巧有如下几种:

(1)同心圆的圆系方程为(x-a)2+(y-b)2=λ2(λ>0)或x2+y2+Dx+Ey+λ=0.

(2)设直线l与圆C相交,则有过直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0.特别地,当l与C相切时,上述方程依然成立.

(3)与直线l:Ax+By+C=0上一点P(x0,y0)相切的圆系方程为(x-x0)2+(y-y0)2+λ(Ax+By+C)=0.

(4)设圆C1与圆C2相交,则过圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0.特别地,当λ=-1时,上方程则退化为过圆C1与圆C2交点的直线方程.

除了上述常见的构造圆系的技巧以外,通过描述圆心的轨迹以及半径的特征也可获得相应的圆系.武汉市2022届二月调研第11题便是一道以圆系为背景的试题,本文将对其进行深入分析,并探究相关的变式问题.

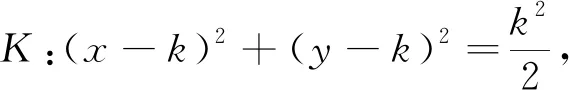
A.圆K过定点 B.圆K的圆心在定直线上

C.圆K与定直线相切 D.圆K与定圆相切

通过上述分析可知,对于圆K,存在定直线与其相切.上述解法主要是通过特殊值验证,再进行理论证明.那么,该结论的几何意义是什么呢?能够通过几何的视角求解呢?

利用上述分析,下面给出几道变式问题.

变式1在平面直角坐标系中,已知圆K:(x-k)2+(y-k)2=λk2(λ>0),其中k≠0,试判断是否存在定直线与圆K相切.

分析：类比上例,通过特殊值验证出所求直线恒过原点,故可设切线l:y=tx,利用切线的判定方法即可求得切线.

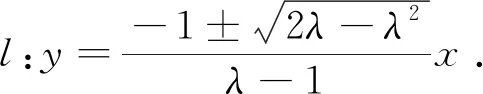
变式2 在平面直角坐标系中,已知圆K:(x-mk)2+(y-nk)2=λk2(λ>0),其中k≠0,试判断是否存在定直线与圆K相切.

分析：与变式1的解法相同,现仅给出结论如下:当λ=m2+n2时,仅存在一条直线与圆K相切;当λ>m2+n2时,不存在定直线与圆K相切;当λ

在上述问题中,圆K的圆心在一条定直线上,若将定直线转化为一般的圆锥曲线,所获得圆系会满足什么性质呢?

变式3 在平面直角坐标系中,已知圆K:(x-mcosθ)2+(y-msinθ)2=r2(m>0),试判断是否存在定圆与圆K相切.

解析:易知圆K的圆心所在的轨迹为x2+y2=m2.当r≠m时,存在两个圆x2+y2=(m-r)2,x2+y2=(m+r)2与圆K相切;当r=m时,存在一个圆x2+y2=(m+r)2与圆K相切.

基于此,我们可以命制出如下的变式.

解析：根据上述分析两圆分别为F1:(x+c)2+y2=(a-c)2,F2:(x-c)2+y2=(a+c)2.其中KF1=RK+a-c,即可知圆K与圆F1外切.因为圆心在椭圆Γ上,根据椭圆的定义,KF2=2a-KF1=a+c-RK.从而可得圆K与圆F2内切.

解析：两圆分别为F1:(x+c)2+y2=a2,F2:(x-c)2+y2=a2.其中KF1=RK+a,即可知圆K与圆F1外切.因为圆心在双曲线Γ上,根据双曲线的定义,KF2=KF1-2a=RK-a.从而可得圆K与圆F2内切.

变式6 已知抛物线Γ:y2=2px(p>0)的焦点为F,已知圆K的圆心在抛物线Γ上,其半径RK=KF,则存在定直线与圆K相切.

证明：设抛物线的准线为l,根据抛物线的定义KF=dK-l的距离.即可得圆K与准线l相切.

除了上述构造变式的方法外,我们还通过限制圆心轨迹的范围来获得特殊图象来命制试题.例如,如图1,已知集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}.由集合P中所有点组成的图形如图中阴影部分所示,中间白色部分形如美丽的“水滴”.下列说法正确的是( ).

图1

A.“水滴”图形与y轴相交,最高点记为A,则A的坐标为(0,1).

B.在集合P中任取一点M,则M到原点的距离的最大值为3.

分析：本题设计的圆系的圆心所在的轨迹为一段圆弧,通过选取特殊位置即可确定“水滴”的关键信息,答案为BCD,过程略.

一般地,圆K:(x-mcosθ)2+(y-msinθ)2=r2(r>m,0<θ<π)所围成的图象均可形成一个“水滴形”的图案.