“风扇模型”的认识与推广

广东省汕头经济特区林百欣中学 (515000) 王晓川

在圆锥曲线问题中,常常涉及到焦半径的性质与命题.若过同一个焦点的多条焦半径,当焦半径的端点为动点时,其形象类似于一个“风扇”,本文将此模型称为“风扇模型”,其中的焦半径称之为“扇页”.特别地,若相邻焦半径的夹角均相等,则称其为“标准风扇”.此模型在高考中的时常出现,值得探究.

一、“风扇模型”及相关定值

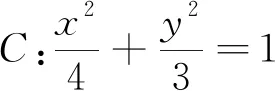
若将焦半径的个数称为“风扇”的级数,上述两题均为三级风扇的考察.通过比较可以看出,题1即为“标准风扇”模型的考察,而题2则是一般“风扇模型”的考察.解决此类问题的核心是利用横坐标以及倾斜角等因素表达出焦半径,再将其转化为其他量的运算.文[1]中利用极坐标为工具研究得出如下三条性质:

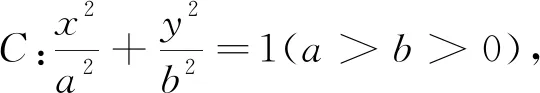
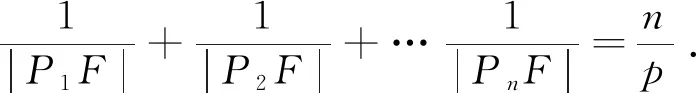
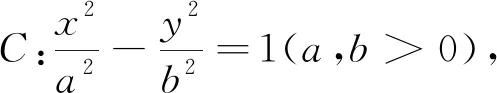
二、“扇页”线性组合后的最值问题

我们可从两个角度对该模型进行分析:一是改变“扇页”的组合方式,求解相应的最值;二是将上述圆锥曲线换成其他封闭的曲线,研究风扇模型是否存在定值,则得到标准“二级风扇”(即过焦点的焦点弦所形成的两个焦半径所形成的“风扇”)的线性组合性质.

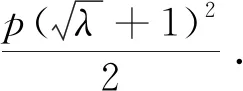
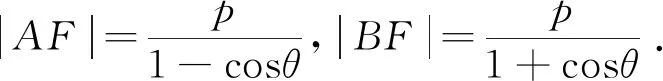
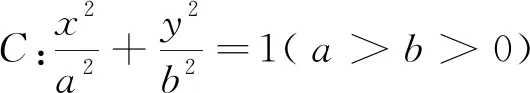
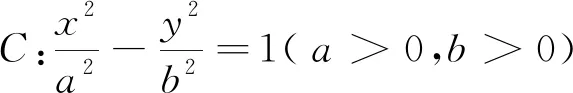
证明类同性质5,此略.

三、正方形内的“风扇模型”

(一)“一级风扇”

为了简化讨论的对象,设正方形ABCD的中心为原点O,设点P是正方形ABCD上的动点,讨论OP的变化规律.

如图2,设正方形ABCD的边长为2,AD,CD的中点为E,F.根据正方形的对称性,可仅考虑点P在ED上的运动规律即可.

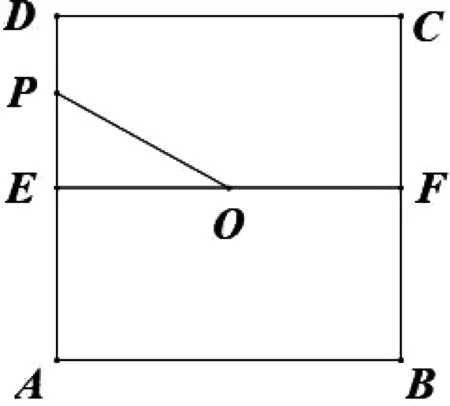
图2

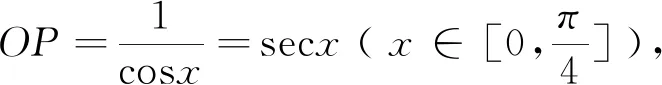
在近几年的高考试题中也出现了该模型的应用.例如,(2015高考新课标2,理10)如图3,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x．将P到A、B两点距离之和表示为x的函数f(x),判断y=f(x)的大致图像

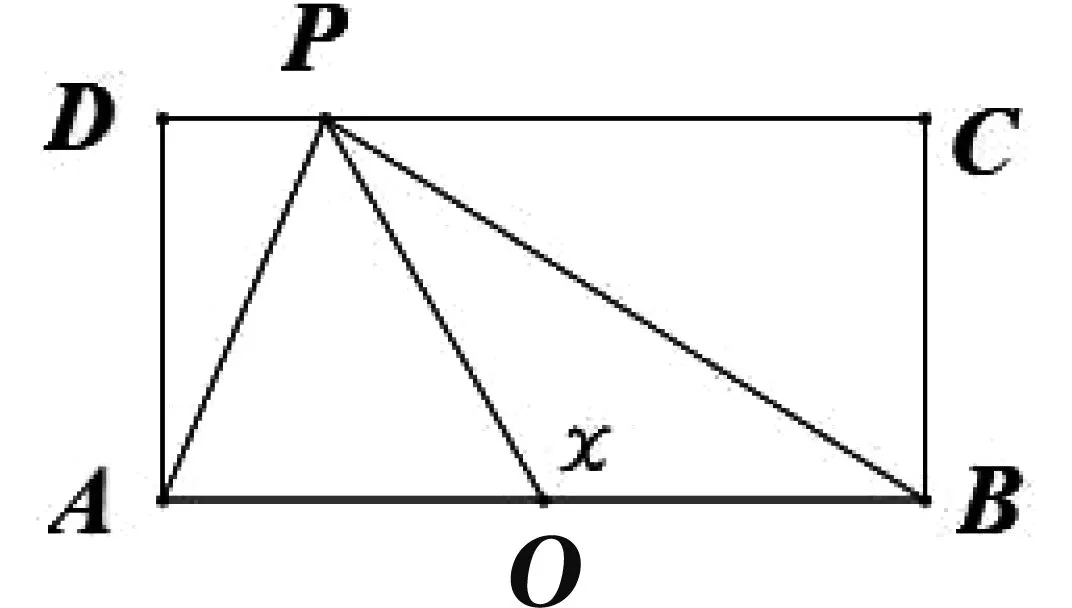
图3

(二)“三级风扇”

根据正方形的对称性,对于标准的“二级风扇”可视为“一级风扇”的2倍,其规律与“一级风扇”相同.接下来,考虑标准“三级风扇”的相关问题.

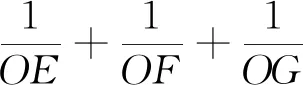
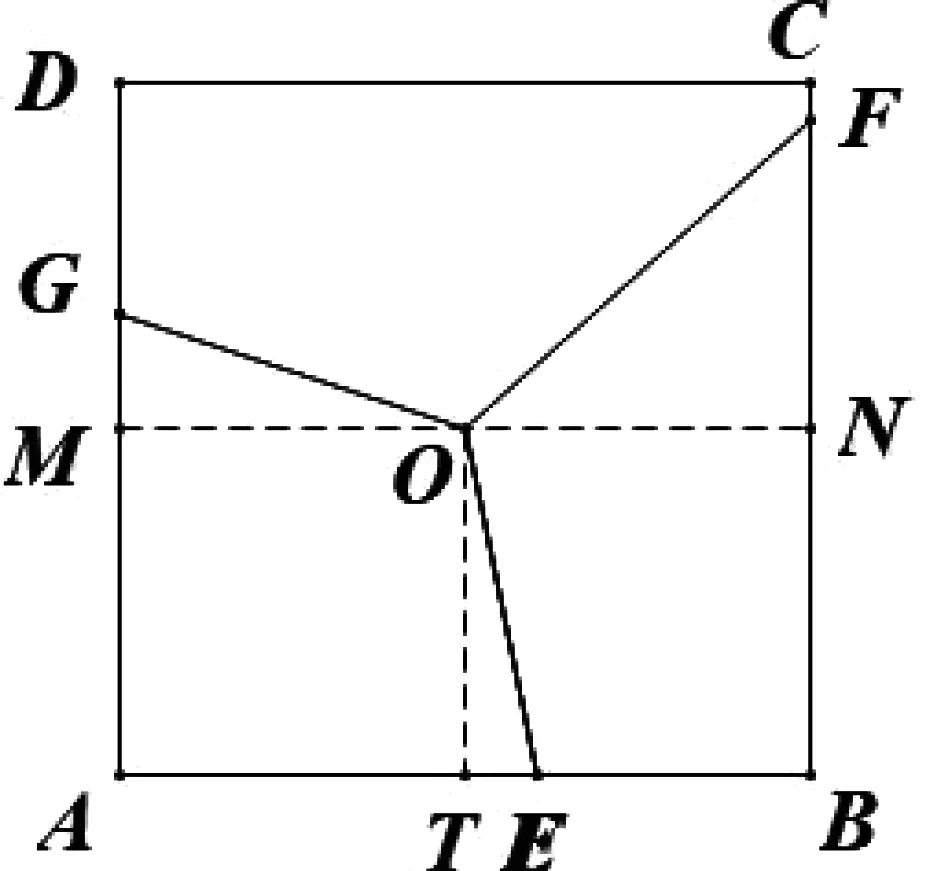
图4

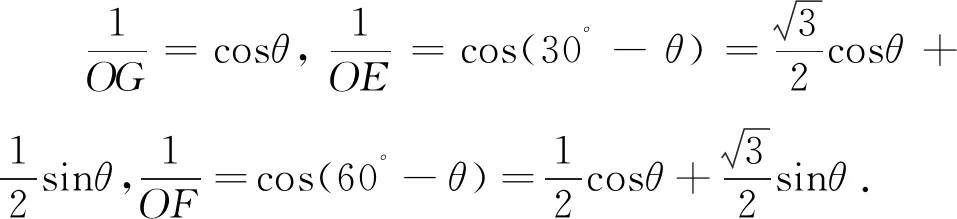
同理,可根据上述思路研究更多级的“风扇”,感兴趣的读者可作继续研究.需注意的是,当外围图形为正方形时,对应的“扇页”并不存在定值,但可根据该模型研究出很多衍生的问题,例如对上述“三级风扇”继续研究ΔEFG的周长及面积等问题.