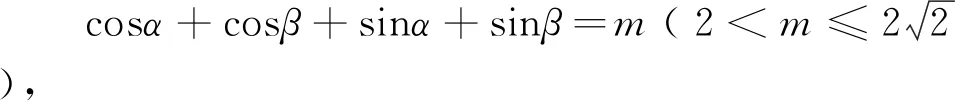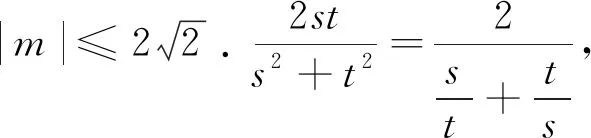一道源于教材的习题探究

广东省佛山市顺德区第一中学 (528300) 杨承根

教材是学生学习的主要材料,好的高考题应该是源于教材.所以在平时的教学中,我们应重视教材,用好教材.在笔者的教学过程中,就对一道教材上的习题进行了深入的探究,现将研究过程展示如下,以飨读者.

一、探究缘起

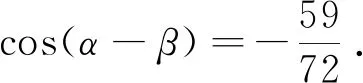
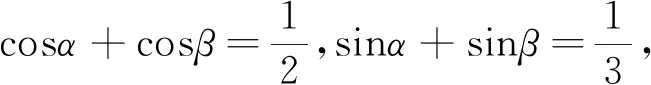
在上述解法中,计算过程均正确,错误的根源在于sin(α+β)正负值的判断.在上述解答过程中可知α+β,α-β的余弦值均为唯一值.而如何判断其正弦值的正负呢?一般解法在于求解出α,β的正、余弦值,再进行求解.此法的运算量太大,且忽略了三角函数的相关性质.为此,笔者从如下六个角度对该问题进行了分析.

二、解法分析

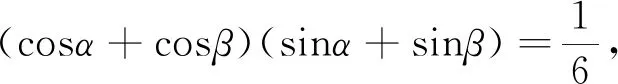
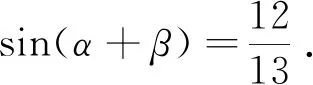
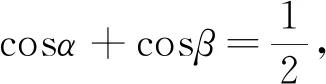
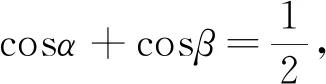
评注：上述四种解法的本质均值在对两个条件进行等价变形,充分地利用恒等变换的相关公式,要求学生熟悉相关的公式并能够灵活运用.

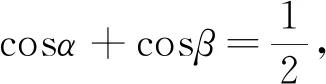
评注：该解法将三角函数问题转化为等差数列,最终通过解方程求得结果,形式虽然新颖,但其本质仍是利用同角函数的性质.其亮点主要在于沟通了两个知识板块之间的联系,但转化后的运算量较大,不易于推广至一般情况.

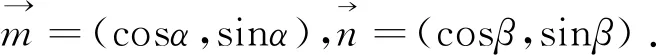
评注：与上述解法相比,该解法通过几何的角度进行解释,直观明了,运算量小,且易于推广.

三、背景探究及变式推广

前四种解法的关注点在于条件的变形,以及和差化积等公式的运用上.其本质上是相同的,但并不能说明所求式是否有两解.解法五属于构造证明,若继续求解可求出所有角的三角函数值,但也不易于推广.解法六通过构造向量及单位圆,从几何层面进行解释,可以很好的解释其存在唯一解的原因.我们还可以基于解法六探究该问题的一般形式.

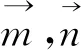
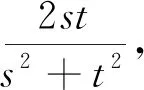
基于上述分析,还可编制如下变式.