精心设计问题,让知识自然生长*
——以微专题研学课例《同构》教学设计为例
2023-05-10江苏省如东高级中学226400朱明明
江苏省如东高级中学 (226400) 朱明明
同构作为一种重要的数学解题方法,在解决一些数学压轴试题时大显身手,以其精巧的结构同化构造化繁为简,起到“四两拨千斤”的效果.因此,同构方法也越来越引起广大师生的重视.然而,笔者发现,在教学实践中,大多老师往往给出若干种固定的同构模型,把同构方法作为一种变形技巧要求学生掌握,让学生通过套用现成的同构模型去解题.这种做法虽然有一定的效果,但由于学生并未真正理解知识源头与生成过程,在遇到陌生问题时学生往往手足无措,一筹莫展.笔者在教学中探索通过精心设计问题,让“同构”知识通过学生的自主活动自然生长,使学生在同构知识研学的过程中思维达到应有的深度,收到了较为理想的教学效果.现将教学案例记述如下,与同行共同探讨.
1.从简单问题入手,让学生感受同构方法魅力
先看两道大家熟悉的问题(投影):
问题1 已知两条直线a1x+b1y+1=0和a2x+b2y+1=0都经过点A(1,2),求经过两点P1(a1,b1),P2(a2,b2)的直线方程.
问题2 若2x-2y<3-x-3-y,则( ).
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
第1题在学生求解的基础上引导学生发现a1+2b1+1=0,a2+2b2+1=0两式的结构相同,进而依照此结构构造一个使得点P1(a1,b1),P2(a2,b2)的坐标均满足的方程x+2y+1=0.第2小题通过将条件2x-2y<3-x-3-y中的变量分离,得2x-3-x<2y-3-y(*),学生观察两边结构构造函数f(x)=2x-3-x,显然f(x)在R上单调递增,(*)即f(x)
2.问题深化,让学生理解同构的底层逻辑
投影例1,让学生先思考.
例1(1)(2022届南京、盐城高三二模)已知实数a,b∈(1,+∞),且2(a+b)=e2a+2lnb+1,e为自然对数的底数,则( ).
A.1 C.2a 引导学生进行思路分析:观察到所给条件中有两个变量,首先考虑将变量分离,即e2a-2a-1=2(b-lnb-1),注意到方程左边为指数式和多项式的形式,右边为对数式和多项式的形式,可以考虑指对互化.将等号右边的b改写为elnb,从而有e2a-2a-1=2(elnb-lnb-1).注意到式子的结构特征——相同结构,联想到构造函数f(x)=ex-x-1(x>0),利用f(x)在(0,+∞)上单调增且f(x)>0,得f(2a)=2f(lnb)>f(lnb),所以2a>lnb,即b 接着让学生再反思:为什么要将等号右边的b改写为elnb?学生发现目的是为了构造出结构相同的式子.那么,还有没有其它的构造方法?引导学生观察:刚才是将等号右边化为与左边相同的形式.能不能右边不变,将左边的式子向右边靠拢?即将2a改写成lne2a,然后构造函数g(x)=x-lnx-1(x>1)即可. 在解决了变式问题后,指对同构的本质就是转化——灵活运用两个恒等式x=elnx以及x=lnex将指对共存的式子化成同一种结构形态,从而确定同构函数,利用单调性等性质解决问题.变形过程中有时需要结合移项、通分、对两边同时加(或乘)某式、取对数等手段. 例2 (2020年山东卷理21题)已知函数f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范围. 思路分析2:(构造函数F(x)=xlnx) 通过本题分析引导学生发现,在指对共存型的恒成立问题中巧妙地使用同构法,能够大大地简化解题过程、回避繁琐的计算.思路1先根据指对式的一致性(互化)进行变形后,发现式子中局部的一致性,进而进行同构;思路2和3则是先通过局部运算对式子进行整理,然后再利用指对式的一致性进行变形得到同构形态.同构法重在观察,巧在构造,质在转化.从某种意义上来讲,指对的跨阶同构最根本的思想是转化与化归,从局部的运算、变形,到适当的配凑,最终达到转化成“同一结构”的目标. 同构作为一种“巧妙”的解题方法,实则通过分析代数式的结构特征,揭示式子间的内在联系,挖掘其中蕴藏的同型与共性,并通过构造相同(或相似)的结构模型实现问题的求解,从而同构法在解方程(不等式)、证明不等式、比较大小、数列乃至解析几何等方面都有着广泛的应用.本节课从教材习题出发,从简单的问题入手,让学生在感受同构的方法魅力的基础上将问题进一步深化,让学生在仔细观察其外形结构的基础上深入剖析其本质属性,理解同构的底层逻辑,有利于学生把握同构转化的内在本质;最后通过高考真题赏析,让学生领略同构的别样风采.这样的处理方式,让学生从知识的底层逻辑剖析,有助于培养学生观察能力、想象能力、构造能力和创新能力,有效提升学生的数学学科素养.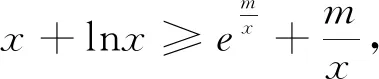
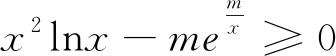
3.真题赏析,让学生领略同构的别样风采