对比中寻找差异 差异中达成共识——以一节微专题复习课为例

安徽省合肥市第四中学 (233000) 李 敏 管良梁

解三角形是高中数学教学的一个重要内容,也是高考的热点之一.解三角形周长范围问题是解三角形问题的一部分,由于涉及的知识点多,灵活性大,综合性强,往往成为学生的难点.因此,在高三二轮复习过程中,可安排一节微专题课.本微专题通过学生对一道例题分析、书写,回忆解决这类问题的两种方法,同时对学生练习中出现的不同解答进行对比,在对比中寻找不同解答的差异,对差异产生的原因进行分析,最终达成解决这类问题的共识.

1 例题解答

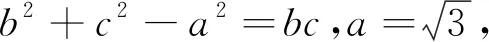
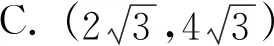
教师：哪位同学来说说你的想法?

学生1：利用余弦定理求得A的值,再利用正弦定理将b,c分别用sinB和sinC表示出来.根据条件和所求的A值,将C用B表示出来,最后用辅助角公式将b+c表示成关于B的三角函数.根据B的范围求得b+c的取值范围,这样就可以求得ΔABC的周长的取值范围.

教师：分析的很好,请把解答过程写在黑板上书写下来.还有其他的解法吗?

教师：分析的很好,也请你把解答过程写在黑板上.

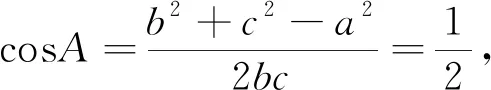
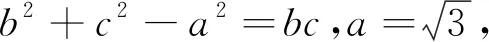
教师：通过两位同学的分析,我们在此回忆了求三角形的周长范围问题常规方法有两种:一是依据题意建立目标函数,利用目标函数的有界性求解;二是依据基本不等式的性质求解.

教师对两位同学的书写进行点评,针对学生1的解答过程强调B的取值范围,针对学生2的解答过程强调不等式等号成立的条件.

2 反馈练习

已知锐角ΔABC内角A,B,C所对的边分别为a,b,c,若a=1,2acosC+c=2b.

(1)求角A;

(2)求ΔABC周长的取值范围.

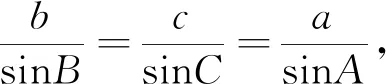
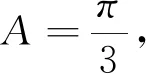
学生4的解答：(1)略(与学生3的解答基本一致).

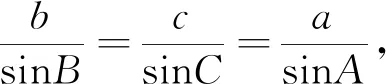
将学生3、学生4和学生5三位同学的解答过程用多媒体同屏展示,并进行对比.

教师：哪位同学来说说,同学3和同学4两位同学解答的差异?

学生6：方法上有差异,但是结果一致.

教师：同学4和同学5两位同学解答过程有什么不同?

学生7：方法一致,但是结果不同.

教师：通过对三位同学解答过程的对比,到底哪位同学的解答过程是正确的呢?

学生：(学生齐答)学生5.

教师：对比例题和反馈练习,已知条件有什么差异?

学生8：例题是在任意三角形下进行的,反馈练习是在锐角三角形下进行的,所以条件不同.

教师：任意三角形和锐角三角形,对我们解题有什么影响吗?

学生9：如果依据题意建立目标函数,利用目标函数的有界性求解的话,就需要注意角的范围.因为是锐角三角形, 所以三个内角都是锐角,根据这个条件缩小自变量(角)的范围.如果根据基本不等式的性质来求解的话,就需要注意受到三个角都是锐角的影响,两边之和不止大于第三边.如果在锐角三角形中还是应用两边之和大于第三边的话,就会使得b+c的范围变大.

教师：回答的很好,通过对学生4和学生5的解答的对比,很容易发现,锐角三角形使得两边之和的范围缩小了.我们也可以借助图形来理解锐角三角形中两边之和范围的变化.

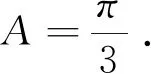
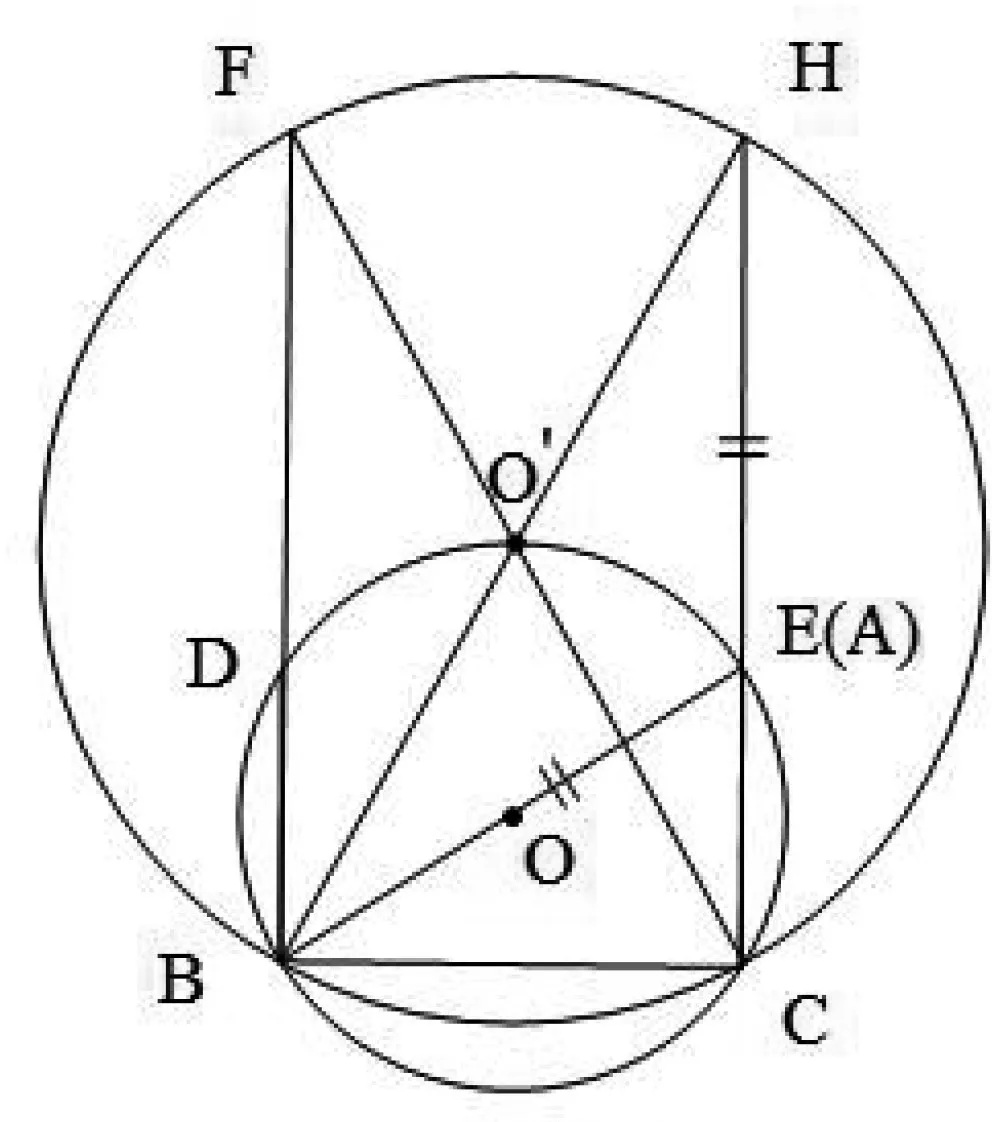
图1

教师：通过前面的对比、分析,你有什么感悟呢?

学生10：以后遇到这类问题时,如果是任意三角形两种方法都可以,最好是应用方法二,因为方法二的计算量要小一些.如果是锐角三角形,就应用方法一,这样准确率要更高一些.

教师：回答的很好.

3 教后反思

3.1 以学生为主体

通过一轮的复习,学生大都能掌握基本知识、基本技能、基本方法和基本思想,有了一定的解题能力.因此,在二轮复习中教师要放手,让学生自主学习.在学生解答出现问题时,教师要及时帮助他们分析问题所在,帮助他们把所学的知识连成线,铺成面,制成网,梳理出知识结构,使之有机的结合在一起.

3.2 认真细致审题

解题的第一步就是审题,认真细致的审题是成功解答的前提.很多学生不重视审题,很多时候还没有弄清问题就进行解答,导致解答错误而丢分.通过认真细致审题了解问题的条件和结论,通过认真细致审题充分挖掘每一个条件的内涵和隐含的信息,发挥条件的解题功能.

3.3 规范解答过程

答题时书写要规范整洁,注重解答步骤完整性,必要的证明过程和演算步骤不可缺少.在二轮复习中要将规范答题落到实处.要养成良好的答题习惯,做到答题规范,需要从点滴做起,重在平时坚持不懈.