中职阶段数学中Geogebra应用的一些案例分析

2023-05-06赵谊阳

科技风 2023年12期

摘要：本文旨在分析中职阶段数学中一些Geogebra应用教学案例，探究Geogebra在中职阶段数学应用中的特色及其优势，思考如何在中职学习阶段数学中更好地使用。

关键词：中职数学；Geogebra；教学案例；函数向量；立体几何

本文重点探讨的重点是Geogebra在中职阶段应用教学中的案例及其分析。与传统的教学手段进行对比，Geogebra软件在代数和几何上展现了强大的教学功能，在基础教育中的教学中有很强的应用能力。通过数形结合，学生可以直观地了解数学知识，并且在数学学习中激发中职学生学习数学的兴趣，在Geogebra的帮助下，可以更有效率地进行学习。

1 中职数学教学常用软件介绍

在目前的数学教育中，比较常见的数学辅助软件有mathtype、几何画板、mathmatica。其中mathtype用在平时编辑数学符号，它缺乏几何作图能力，有着不小的弊端。几何画板可以进行作图功能，但是在计算代数上相对有所缺失。mathmatica功能与Geogebra有些相似，但是操作系统过于复杂。Geogebra另一个最大的优势就是软件版权是免费的。

2 Geogebra软件介绍

Geogebra是一款结合代数、几何和微积分的动态数学软件，基于Geogebra软件在代数和几何上的强大功能，其在基础教育的教学中有很强的应用能力。

Geogebra軟件特点如下：

*可免费用于学习、教学和考评。

*功能强大、使用简单、交互性强。

*支持多种语言。

*以趣味的方式真正观察和体验数学和科学。

*可适用于各种课程或项目。

*在世界上有数百万人使用。

3 运用Geogebra软件教学案例

由于Geogebra软件的优势，必然有了让我们利用它上课的可能，这里我们提供一些本校老师在上课时，利用Geogebra软件的一些案例。

3.1 数形的完美应用——向量

Geogebra第三栏中专门有一“向量”图标，通过这一强大功能，为学生建立起向量的模型及其简单应用。

3.1.1 课本7.1平面向量的概念

Geogebra在本节课中的应用：Geogebra第三栏中专门有一个“向量”图标，通过Geogebra，我们可以很简单地用图标画多条向量，并且进行简单的区分，不同的向量之间通过什么进行区分？左图中的向量都是不相同的向量，利用软件的直观性，可以相对简单地体现向量的定义：有方向、有大小的量。通过度量向量长度展现向量的模。

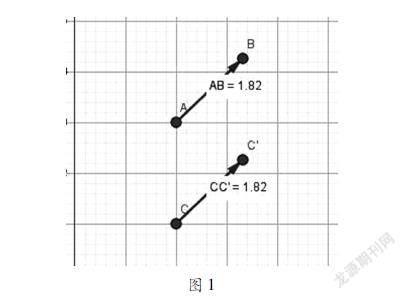
随后可以利用Geogebra软件中的“向量”图标建立相等的量（图1），再次体现向量的大小和方向，即引出相反向量。强调相等及相反向量的共同点——大小（模）相同。

在介绍平行向量和向量共线特点时，可以通过建立平行线，通过平移功能直观体现出平行，在通过向量确定端点的前提下，拉动终点，进行观察向量特征，得出平行向量只和方向有关，和大小无关的特点。

Geogebra在本节课中的应用思考：在向量概念一节课中，利用Geogebra充分体现了数与形的结合，并且还有着信息化教学中的精准，保证了数学的严谨性的同时，方便学生形成向量概念，显著提高了教学的效率。

3.1.2 课本7.2向量的线性运算——加减运算

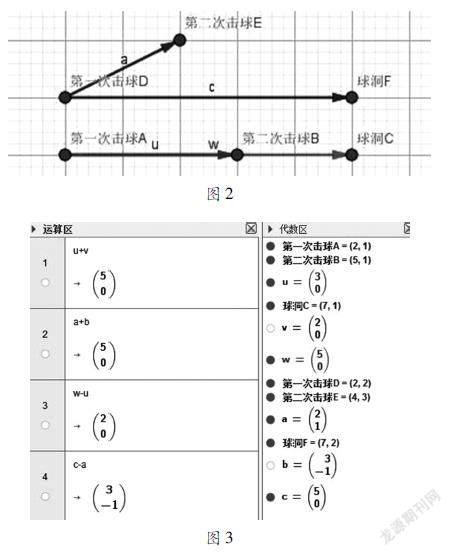
Geogebra在本节课中的应用：在向量的加法、减法运算中，我们要区分平行向量和非平行向量。在我校休闲体育专业中，曾经利用Geogebra演示了高尔夫比赛中的过程，体现了向量的加法特征的同时，彰显出向量在休闲体育专业中的应用。能够理解向量运算的本质，引入合理击球的概念、和向量——击球点到球洞、加向量——第一次击球和第二次击球，通过用Geogebra可以很直观描述出两个向量的和运算本质，如图1两种情况：平行的和向量：u→+v→=w→，不平行的和向量：y=x-12。通过击球建模向量配合Geogebra的图像展示向量的和计算。

学生对于认识图形是一种直观认识，而同样的图形，我们可以通过不同对应的变式引出减法的特征。如图2和图3，教师可以这样提问，观察左边的图形向量w（c）是正确的进洞轨迹，向量u（a）是第一次击球，问如何表示出第二次击球向量v（b）。对于学生而言，向量v是很容易出现概念的，而可以很容易让休体班的学生自己归纳出向量v是作为差向量出现的，v→=w→-u→/b→=c→-a→。在试着擦去另一个向量u（a），可以让学生归纳出另一个向量关系。最后在总结和向量和差向量关系的时候，利用Geogebra很容易由v→+u→=w→推出另两个v→=w→-u→和u→=w→-v→，得到被减向量和和向量之间关系。在建立了向量思维模型后，引入代数知识就相对比较简单了，达到了由形到数的转变。

Geogebra在本节课中的应用思考：向量加减的计算分为数的运算和几何意义。而难度较大的是几何意义，而Geogebra可以方便形象地进行教学和帮助学生建模，而在数的运算和单位向量的求解上更是便捷和准确。缺点就是利用了Geogebra后，运算难度降低，学生在思维上会产生一定的惰性。

球员比赛的击球路线，展示出击球及其轨迹并利用Geogebra用向量模拟。

3.2 图形中的美丽——立体几何

可以这么说，立体几何才是我们教师利用Geogebra的主场。本章节重难点是在认识棱柱、棱锥、圆柱、圆锥、球及其简单组合体的结构特征后，引导学生运用这些特征描述实际中简单物体的结构，从而使学生把学习的眼光从课堂延伸到更广阔的生活实际中去。可以利用Geogebra完成图形的建立，确定图形的大致结构寻找出对应的立体几何。在这里我们以我校陆老师在开设的一节三视图学习的公开课作为案例进行探讨和分析，如图4。

Geogebra在本节课中的应用：美术设计班的同学在设计亭子时遇到了困扰，利用数学三视图知识，结合Geogebra软件进行辅助指导完善学生作品。

在本节课中学生首先分组完成了通过收集亭子素材——素描亭子——Geogebra制作亭子，让亭子能够在电脑中具现出来。在这一过程中，学生在原有相对抽象的艺术形态素描里对亭子进行了进一步整理，在制作过程中虽然也有着很多不足，但是在互相帮助和指导中，学生明显对自己设计的亭子有了更多的了解。

回顧设计要求，再通过改变三视图的长、宽、高，利用Geogebra所作三观图一一对应，确保设计合理和达到标准。进一步修改亭子中占地面积——俯视图、可容纳休憩的人数对应椅子的坐宽——左视图、亭子的合理高度——主视图。学生的专业知识和问题充分结合了Geogebra的强大功能，利用数学知识处理实际问题。

Geogebra在本节课中的应用思考：通过Geogebra展示改善了教学内容的呈现方式，在3D绘图区，能够把立体几何图形完整、360度无死角地体现出来，让学生对于简单组合体有了更加直观的认识，并且可以通过建模后，处理一些比较简单的数学问题。

在整个立体几何章节中，Geogebra完全可以大展拳脚。Geogebra在画棱柱、棱锥、圆柱、圆锥、球及其简单组合体方面有着其独特性。首先，Geogebra在画立体几何图形时，有着多元化的特征，可以通过做底面直接拉成一个棱柱，同样也可以通过确定几个点分别确定底面和高制作棱柱。在作图过程中方法的多样性，让学生有多种选择之余，可以进一步了解图形的结构特征并反馈到作图过程中。其次，Geogebra作图能给学生和教学带来无比的便捷性，与手绘作图相比，速度有了明显提高。最后，Geogebra作图基于程序的特征有着百分之百的正确性。

3.3 数学的基石——函数

可能有人会很奇怪，为什么会把函数放在最后？因为函数是数学的基石，没有函数数学的骨架就没了。一个合格的数学辅助教学软件，函数可以说是必不可少的一部分，但是也是最能体现差距的一部分。让我们来了解一下Geogebra在中职教学中的应用。

Geogebra在课本3.3简单幂函数这节课中的应用：

本节课是在让学生预习了幂函数定义的前提下进行的，观察幂函数y=xa（-5

最后利用Geogebra再简单介绍y=x12、y=x-12的性质，帮助学生做一个简单补充。

课后作业要求每一个学生制作符合4种情况的Geogebra幂函数图像。

Geogebra在本节课中的应用思考：本节课，学生在绘制过程中利用Geogebra的快速呈现函数图像并且易于操作的特点，让学生在自己动手的前提下，充分感悟几个简单幂函数的性质，并且加深理解。

在函数教学利用Geogebra进行教学中，有如下几点全面性。

3.3.1 内容全面性

中职阶段的函数简单幂函数、指数函数、对数函数和三角函数，初中阶段的正比例函数、反比例函数、一次函数和二次函数，都能够在Geogebra上表示出来，通过软件能够简单明了地体现出函数图形和函数特征。Geogebra是学生构建模型的最好方法。

其中幂函数是最多变的函数，在实际教学中，我们完全可以通过滑动条改变指数，体现出不同幂函数的特征，帮助学生学习和归纳。

3.3.2 性质的全面性