铅蓄电池充放电建模与仿真

杜春雨 姜海龙

摘 要：根据铅蓄电池的结构与充放电特征，本文研究了铅酸蓄电池的三阶动态模型，并结合其充放电特性对模型进行了适度简化，建立了铅酸蓄电池的充放电模型。采用Simulink仿真软件，对不同环境温度下铅蓄电池充放电的全过程进行了仿真。仿真结果显示，本文提出的模型能够较准确地反映蓄电池在不同环境温度下的充放电特性，可为铅酸蓄电池建模仿真研究提供参考。

关键词：铅酸蓄电池；三阶模型；全过程仿真；Simulink仿真

中图分类号：TM411；TP183  文献标识码：A  国家标准学科分类代码：470.4017

铅蓄电池技术相对成熟、性能可靠、廉价、使用寿命长，维护工作相对容易。不但通常会作为潜艇水下电源、辅助电源和应急电源使用［1］，在变电站及二次电池市场中也占有举足轻重的地位。

蓄电池是一种具有较高效率的能源转换装置，经常被当作电力系统中的重要储能设备，其性能对潜艇安全具有重要影响［2］。从蓄电池使用角度看，影响蓄电池性能劣化的主要因素有：过充电、过放电、长期处于低荷电状态等［3］。

环境温度会影响蓄电池的充放电特性，对蓄电池开展动态仿真，有利于准确地把握蓄电池的性能。常用的蓄电池模型包括电化学模型和等效电路模型。在这3种模型中，等效电路模型最适合开展系统动态特性的仿真研究。本文采用简化后三阶动态等效模型对蓄电池进行建模，并对其在不同环境温度充放电过程进行仿真分析，研究蓄电池在不同环境温度下的充放电特征之间的关系，并通过Simulink对所建立的模型进行仿真验证，结果证明了本文所提模型的正确性。

1 铅蓄电池等效电路模型

等效电路模型是将蓄电池等效为由电压源、电流源、电阻、电感、电容等理想元件串并联所构成的等效电路，利用电路的电能分配关系，模拟蓄电池的充放电特性。目前常见的等效模型电路有：Rint模型、Thevenin模型、三阶动态模型和四阶动态模型［1］。

Rint模型是將蓄电池等效为理想电源和等效内阻的串联，其电路过于简单，无法反映出电池内阻随电解液、温度、电池容量的变化过程，只能用于不考虑SOC和温度的场合。Thevenin模型将内阻分为极化内阻和欧姆内阻，考虑了充电过程中的计划现象［5］，但是模型的参数都是参量，没有考虑SOC、温度和自放电的影响。四阶动态模型中涉及的经验参数过多，计算过于复杂［4］。

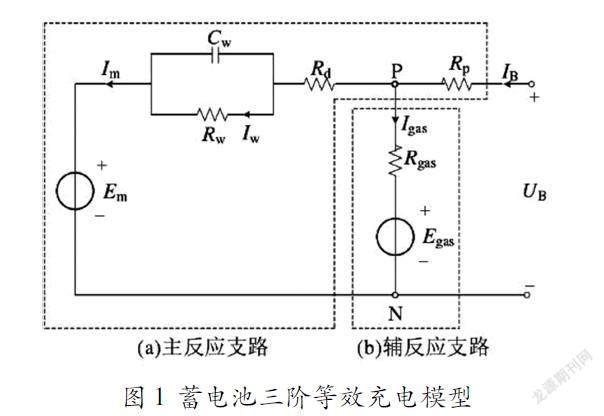
由图1可知，三阶模型包括主反应支路以及辅反应支路。主支路包括电动势Em、RC电路（由扩散电阻RW和扩散电容CW和组成）、电荷转移电阻Rd和欧姆极化电阻Rp。主反应支路反映了蓄电池在充放电时的电极反应、能量散发和欧姆效应。

蓄电池充电时，能量由电能转化为化学能。当充电几近完成时，蓄电池中的活性物质全部消耗完毕，开始发生水解反应，即电解析气反应。辅反应支路用来反映主要反映蓄电池的水解反映及自放电现象，图1中表示为Igas流过的支路，Rgas、Igas、Egas没有特殊的物理意义。

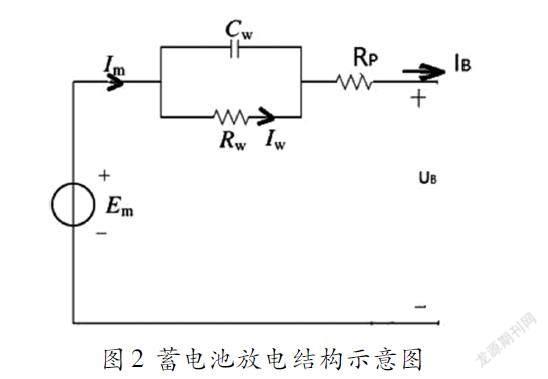
蓄电池放电时，Rd和Igas接近于0。因而，蓄电池的放电过程，可以不用考虑辅反应支路的影响。模型可以进一步简化，如图2所示：

2 铅蓄电池数学模型

2.1 蓄电池的动态模型

将蓄电池的电量Qe和电流Im作为状态量，根据图1中，RW和CW的关系，可以得到RC电路的二阶动态方程，见式（1）、式（2）。

dQedt=-Im（1）

dIWdt=1τ（Im-Iw）（2）

式中，τw=Cw·Rw为时间常数，一般取为7200s。Im=IB-Igas，放电时，Im=IB。

在蓄电池充放电的过程中，电解液温度会发生变化，从而影响电池的内部参数，因而需要对电解温度进行计算。假定电解液分布均匀，将电解液温度θ也作为一个状态量，得到温度的动态方程，见式（3）。

dθdt=1Cθ（PB-θ-θaRθ）（3）

式中，Cθ是比热容；Rθ是电池与环境之间的热阻；θa是电池在周围的环境温度；PB是电池内部电阻消耗的功率。

联立式（1）～式（3），可以得到蓄电池的三阶动态方程。

2.2 参数计算

要求解式（1）～式（3），需要求解PB、UB、Igas等参数。

根据图1的电路原理，蓄电池的损耗PB和端电压UB可以分别表示为式（4）和式（5）：

PB=I2BRP+I2mRd+I2wRw（4）

UB=IBRP+ImRd+IwRw+Em（5）

UB和IB分为蓄电池的端电压和电流，由外部的充放电电路决定。

依据能斯特方程［6］，蓄电池的电动势Em与随着荷电状态SOC增加而升高，并且与电解液的温度θ相关，可表示为式（6）：

Em=Em0-Ke（273+θ）（1-SOC）（6）

式中，Em0为蓄电池满电量（SOC=1）时，蓄电池的开路电压KE为经验系数。

电荷转移电阻Rd和欧姆极化电阻Rp与荷电状态SOC有关，扩散电阻RW与充电深度DOC有关：

Rp=Rp0［1+A0（1-SOC）］（7）

Rd=Rd0*exp［A21*（1-SOC）］1+exp（A22*Im/IBN）（8）

Rw=-Rw0ln（DOC）（9）

式中：Rd0，Rp0，RW0，代表蓄电池满电量时的电阻；A0，A21，A21都是常数，IBN是额定电流。DOC表示电池的充电深度，也可以用来表示剩余容量。

一般采用荷电状态SOC表示蓄电池的剩余容量，多采用安时计量法进行实时估算。假设蓄电池最初荷电状态等于SOC0，电池充满电时等于1，SOC可以表示为式（10）［78］：

SOC=SOC0-QeC（0，θ）（10）

蓄电池实际容量C（IB，θ）和实际工作电流IB、电解液温度θ以及蓄电池在参考情况下容量相关，具体表达式如下：

C（IB，θ）=KC1+θ-θfε1+（KC-1）（IB/IBN）δC（IBN，θN）（11）

式（10）、（11）中，C（0，θN）是电解液参考温度θN下的额定容量C（IBN，θN）是在额定电流IBN以及电解液参考温度θN下的参考容量，θf为电解液的冰点温度，Kc、δ、ε为经验系数。

电池充电深度DOC为：

DOC=SOC0-QeC（IB，θB）（12）

主反应回路中，在计算电阻的时候，考虑了SOC和DOC的影响，这两个参数都是温度的函数，因而，所构建的模型考虑了温度对蓄电池内阻的影响。

2.3 辅反应支路

辅反应支路用来仿真铅酸电池的电解析气反应。充电将完成时，蓄电池会发生水解反应，析气电流Igas呈指数函数变化，可表示为式（13）～式（15）：

Igas=GgasUPN（13）

Ggas=Ggas0exp［UPNUP0+AP（1-θB/θf）］（14）

UPN=UB-IB·RP（15）

其中，Ggas0、UP0、AP均为经验参数。

3 蓄电池的充放电模型

蓄电池的充放电模型如图3所示，包括：主反应支路、温度模型、辅反应支路、参数计算模块和电量与容量模型。主反应电路是（1）、（2）、（4）、（5），对RC电路进行动态仿真；温度模型是（3），对电解液温度进行仿真；电量模型是（10）～（12），计算荷电状态SOC和充电深度DOC；参数模型是（6）～（9），计算蓄电池的内部阻抗。

模型的输入为外电路的充放电电压UB（电流IB）和环境温度，输出为电解液温度θ、荷电状态SOC和充电深度DOC。蓄电池充电包括恒压充电、恒流充电和涓流充电等3种模式。采用恒压充电时，UB为定值；采用恒流和涓流充电时，IB为定值。

4 仿真结果

在25℃、40℃、50℃的环境温度下，分别对蓄电池进行全充、全放的仿真，结果如图4、图5所示。

图4是蓄电池的全充过程。图中t1，t2，t3分别代表充电的3个阶段。t1阶段是恒流充电阶段，最大充电电流15A；t2阶段是恒压充电阶段，最大电压3.7V；t3是涓流充电阶段，电流为0.3A。模型根据SOC的大小，自动进行充电方式的切换。当SOC在0～60%之间，处于t1阶段；SOC在60%～90%之间，处于t2阶段；SOC在90%以上时，处于t3是涓流充电阶段。

根据仿真结果，在恒流充电阶段，SOC和温度的上升较平稳，这与充电电流是恒定的有关。进入恒压充电后，由于充电电压和蓄电池压差相差较大，充电电流急速增加，电解液温度和SOC随之急增；随后蓄电池与充电电压的压差减小，充电电流变小，电解液温度上升到最高点后开始下降，SOC趋于饱和。

电池温度与环境温度有关，环境温度越高，电解液的温度越高，其充电速度越快，与蓄电池的特性一致。

图5是蓄电池的放电过程，采用0.3A左右放电，放电时间与环境温度有关，环境温度越高，放电越快。

结语

对铅酸蓄电池建模时，需要考虑环境温度、电池结构和荷电状态等多种因素，尤其是环境温度会影响蓄电池内部参数，导致充放电的特征发生变化。此外不同的充电方式下，蓄电池的特性也不尽相同，三阶模型较准确地反映了铅酸蓄电池的结构和特性，为后续研究奠定基础。

参考文献：

［1］徐峰.潜艇用铅酸蓄电池综述［J］.船电技术，2011，31（12）：6061.

［2］侯世英，房勇，孙韬，等.混合储能系统在光伏发电系统功率平衡中的应用［J］.电网技术，2011，35（5）：183187.

［3］宋雷鸣，牟晓卉.浅析影响铅酸蓄电池使用寿命的主要因素和注意事项［J］.電源世界，2009（1）：5556.

［4］王仕龙，宋小冰，杨齐家，等.基于DIgSILENT的蓄电池建模仿真［J］.通信电源技术，2017，34（02）：1719+28.

［5］黄鑫，蓝贤桂.铅酸蓄电池内阻参数等效电路建模及其仿真［J］.电子世界，2020，24（39）：8486.

［6］李军徽，焦健，严干贵，等.铅酸蓄电池三阶动态模型的仿真研究［J］.东北电力大学学报，33（1）：103108.

［7］Stefano Barsali，Massimo Ceraol.Dynamical Models of LeadAcid Batteries：Implementation［C］.IEEE Transaction on energy conversion，2002.

［8］Massimo Ceraolo.New Dynamical Models ofLeadAcid Batteries［C］：IEEE Transactionon Power System，2000.

作者简介：杜春雨（1992— ），男，汉族，山东青岛人，硕士研究生，研究方向：装备保障；姜海龙（1971— ），男，汉族，黑龙江鹤岗人，博士，教授，研究方向：装备保障。