基于迁移学习的辐射源个体识别分类方法

刘 振,陈阿磊,李世飞,袁俊泉,黄 亮

(空军预警学院,湖北 武汉 430019)

0 引 言

辐射源个体识别(SEI)[1-3]技术是针对同一型号、批次及工作方式的不同辐射源,综合分析并提取能有效区分辐射源个体的特征,通过高性能的分类算法来识别具体的辐射源个体的一种方法。在复杂战场信号环境中,可以通过截获各辐射源信号的细微特征来区分信号源个体,进一步锁定并监视辐射源,同时对判定通信网络的组成也能提供有力支撑,具有重要的军事应用前景。在民用方面,为了有效管理频谱环境,相关管理部门需要定位识别那些非法的电磁辐射源个体,如何从众多辐射源中识别出非法辐射源个体则十分关键。

当前,辐射源个体识别技术的研究大多都是在提取特征后,采用传统机器学习进行分类识别的[1-2]。在现实中,辐射源个体特征受时间、空间、应用条件等因素的影响,不同时间段某一辐射源设备具体组网方式、使用情况都不相同,不同时间段获取的数据往往并不完全服从相同分布。在这种情况下,传统机器学习难以取得可靠的分类识别效果。迁移学习[4-6]不需要传统机器学习的这种假设,能够从与目标域不同但相似的源域数据中挖掘有用知识并迁移到目标域学习中,因而得到了广泛的关注和研究。立足于辐射源个体识别应用特点,本文对基于迁移学习的SEI技术开展研究,提出了基于迁移学习的辐射源个体识别分类方法。

1 基于模糊近邻密度聚类和重采样的TL-FNDCReK算法

1.1 迁移学习框架及分析

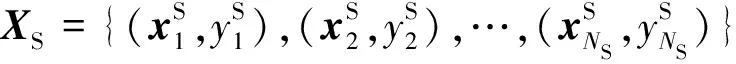
如图1所示,圆形和方形表示2种类别,黑色点表示已标记的训练数据,空心点表示未标记的测试数据。在图1(a)中,由于训练数据与测试数据的分布结构不同,直接使用训练数据学习的分类模型对测试数据进行分类识别,往往具有较高的错误率。基于聚类分析和重采样的迁移学习方法不仅不需要直接估计域分布,且能够修正不同类型的域间差异[7]。图1(b)～(d)给出了迁移学习过程:图1(b)首先通过对整个数据集进行聚类分析,寻找数据结构信息;然后,图1(c)按照一定的策略对每个聚类子类进行数据筛选,选取与测试数据集分布尽可能相似的数据用于分类模型的学习;图1(d)使用重采样的训练数据所得到的模型分类识别效果有了较好的改善。

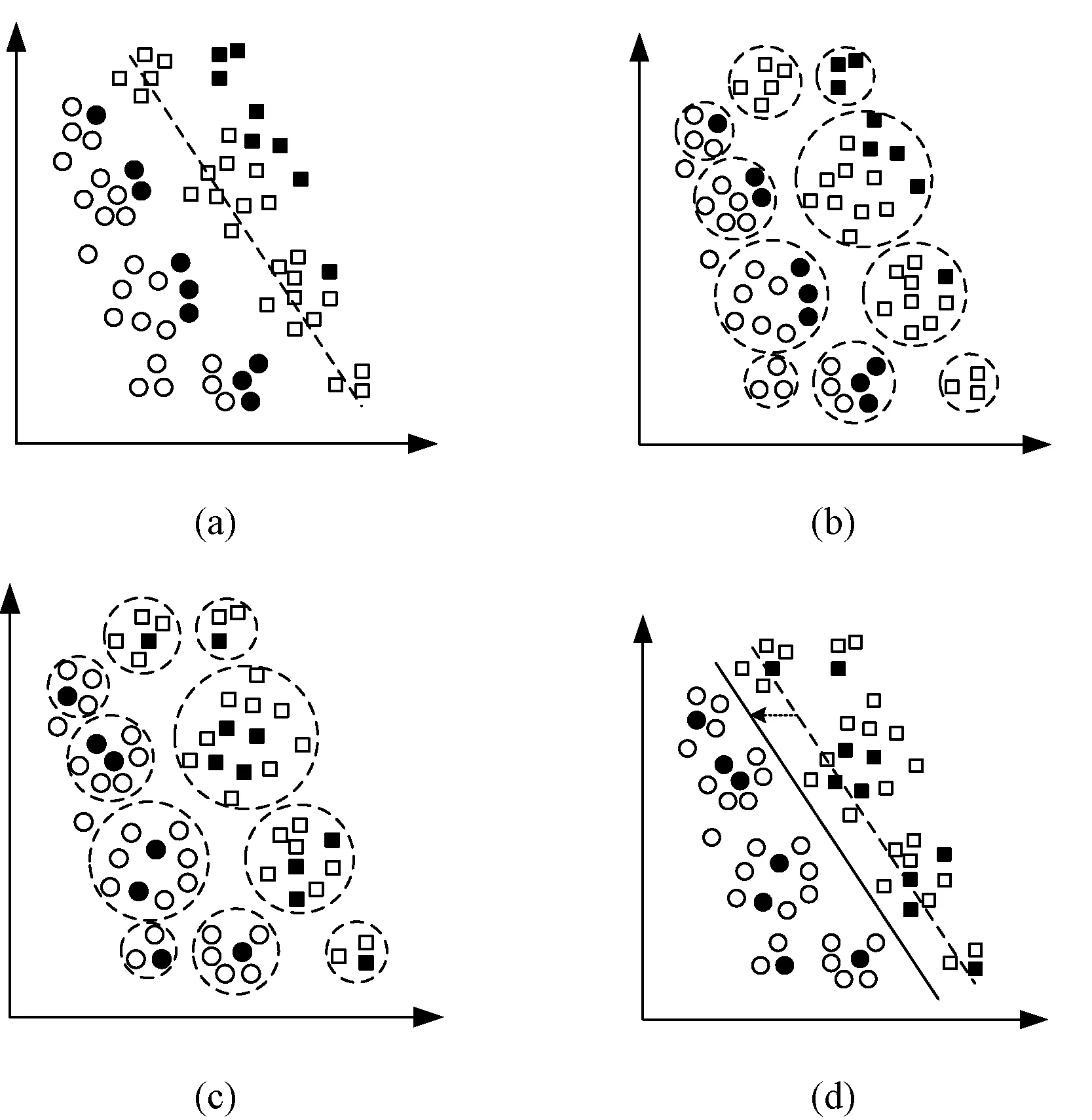
图1 聚类分析与重采样的迁移学习基本思路

如图1(b)所示,通过在总数据集X上进行聚类分析来探求数据的固有结构信息,理论上可以采用任何具有良好性能的聚类算法,如同样使用该迁移学习框架的BRSD(Bias Reduction via Structure Discovery)算法[7]就采用了基于DBSCAN(Density Based Spatial Clustering of Application with Noise)的聚类分析。

DBSCAN算法不用预先设定聚类子类个数,能够挖掘不规则子类数据结构,具有更好的聚类性能。其主要思想是:从某一个核心点开始,然后最大化它的密度可达区域,从而形成一个内部只有核心点和边界点且2点之间密度可达的新子类。如何在整个数据集中发现核心点对DBSCAN聚类的效果十分关键,通常定义近邻个数大于阈值的数据xi为核心点,即满足式(1)的数据点:

(1)

式中:近邻基数C(xi)用于衡量xi近邻集合的大小;门限值T可以通过所有数据点的近邻基数平均值进行估计;M(xi,xj)表示xj对xi的近邻归属度:

(2)

式中:d(xi,xj)表示数据xi与xj之间的距离;r为近邻半径,可利用有标记数据进行近似估计[7]。

如果xj在xi的邻域内,则M(xi,xj)=1;否则为0,故而M(xi,xj)又称为离散近邻归属度,如图2所示。

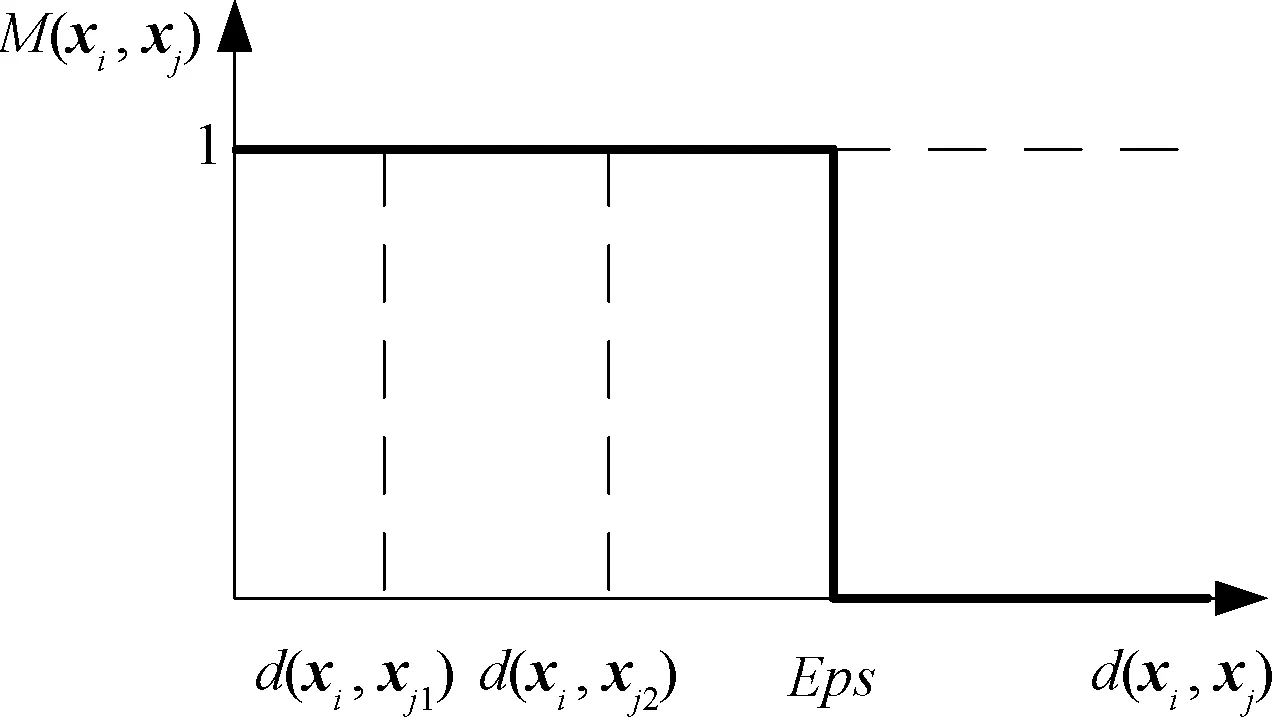
图2 离散近邻归属度

如图2所示,由于没有考虑邻域内数据的距离差别,邻域内所有数据的作用都是相同的,故而无法区分它们的差异性。在图3中,大的实线圆表示邻域边界,xi1和xi2的近邻个数相同但近邻分布不同。由式(1)和式(2)可知,xi1和xi2的近邻基数是相同的,但可以明显看出它们的数据结构不同。利用离散近邻归属度表征近邻关系会造成数据近邻结构信息的丢失,而这种信息可能会对学习具有重要的作用。在图3(a)中,尽管xj和xk都非常靠近邻域边界,它们的离散归属度却完全不同。若邻域半径变为r1,则xi1的近邻基数就会从10变成20;而若邻域半径变为r2,近邻基数会从10变成1,很可能导致xi1从核心点变为非核心点。离散近邻归属度会使算法对参数r的取值过于敏感,进而对不同分布形状和密度的数据鲁棒性较差。但是参数r一般是很难精确得到或估算的,也就导致无法保证算法的性能。

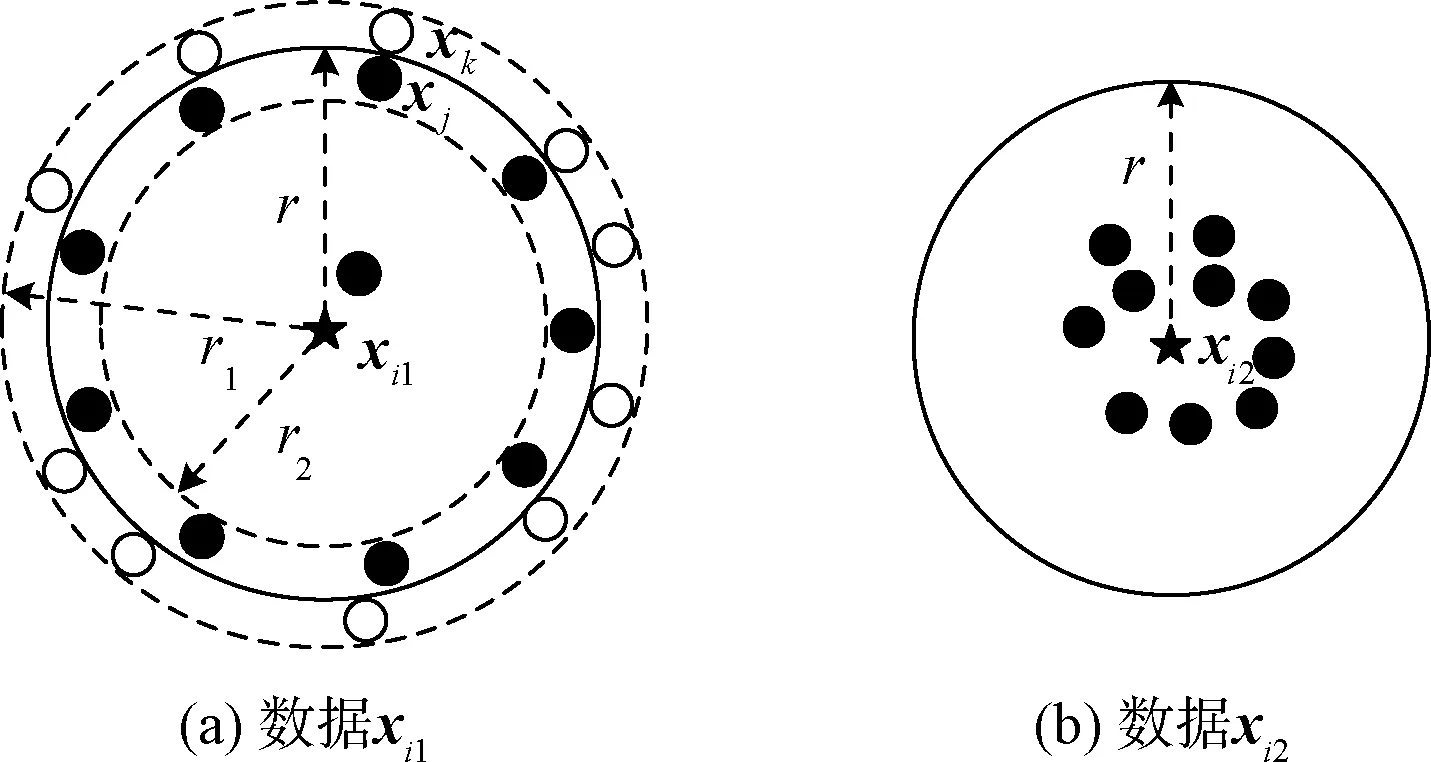
图3 不同数据分布的近邻归属度

1.2 基于模糊近邻密度聚类的数据结构信息挖掘

由于聚类算法的性能对数据结构信息的挖掘至关重要,针对离散归属度在挖掘数据结构信息时存在的缺陷,提出一种基于模糊近邻密度聚类与重采样的迁移学习算法(TL-FNDCReK)。该方法使用模糊近邻归属度[8]代替离散近邻归属度,以更好地挖掘数据结构信息用于目标域的学习。式(3)给出了一种线性模糊近邻归属度:

(3)

式中:β(β>0)用于调节近邻归属度对距离的敏感度,为了使M(xi,xj)在[0,1]内,β一般计算如下:

β=(1-m0)

(4)

式中:m0∈[0, 1],表示恰好处于邻域边界上的数据的近邻归属度。

在邻域内,M(xi,xj)对距离的敏感度与m0的取值成反比。图4给出了线性模糊近邻归属度的示意图。

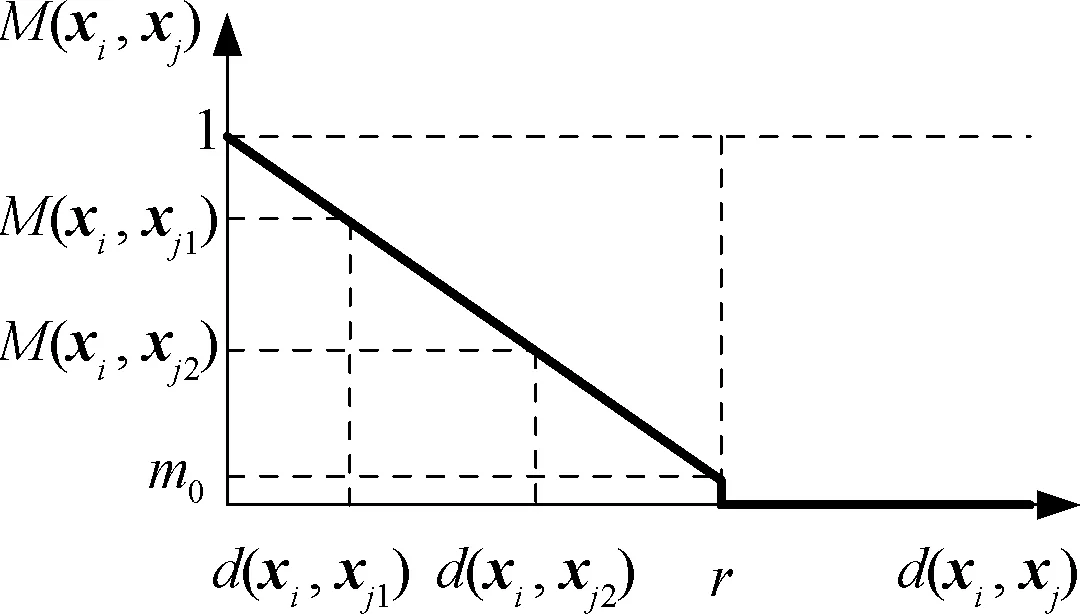
图4 线性模糊近邻归属度

通过式(3)和式(4)的定义,可以看出:邻域内数据点的模糊近邻归属度随着其与中心数据的距离不同而不同,越靠近中心数据,其模糊近邻归属度也越大,据此能够较好地区分邻域内数据的差异性。在图3中,xi2的近邻基数也会大于xi1的近邻基数,更加符合实际的数据邻域结构信息。并且,在图3(a)中,如果m0趋于0,则靠近邻域边界的数据点无论在邻域内外,其模糊近邻归属度都趋于0,参数r的微小变化就不会对整个学习过程造成大的影响,有助于提高算法对参数r的鲁棒性,进而能够适应不同分布形状和密度的数据。

此外,考虑到数据之间可能会存在非线性关系,导致数据距离与近邻归属度的关系也可能是非线性关系,此时线性模糊近邻归属度可能就无法适用。因而,式(5)给出一种非线性的模糊近邻归属度,即指数模糊近邻归属度:

M(xi,xj)=

(5)

式中:调节M(xi,xj)对距离敏感度的参数β(β>0)计算如下:

(6)

式中:m0=(0, 1],表示在邻域边界上的近邻归属度。

图5给出了指数模糊近邻归属度的示意图。

1.3 基于数据标记可信度和代表性的新训练样本重采样

假设对数据集X进行聚类处理,得到聚类子类{C1,C2,…,CNC},其中子类个数为NC,第i个子类的数据个数为NCi。然后进行重采样时,在每个子类Ci中优先选择标记可信度高、数据代表性高的数据[7],选取数据的个数比例一般为源域样本数与总样本数的比值NS/N。首先,从每个子类中选择一定数目(大于NCiNS/N)的标记可信度较高的数据。然后,再从中选择NCiNS/N个数据代表性较高的数据加入到新训练样本集。在遍历完所有聚类子类后,便完成了整个新训练样本的选择过程。数据xi的标记可信度Rl(xi)为:

(7)

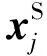
数据代表性Rp(xi)为:

(8)

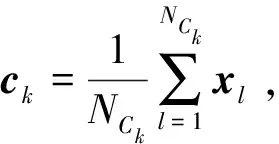
由式(7)和式(8)可以看出,数据的标记可信度和代表性的计算其实就是一种相似性度量,是通过距离dist(·)来表征的,dist(xi,xj)越小,则xi与xj就越相似。BRSD算法计算dist(xi,xi)采用的是曼哈顿距离:

(9)

式中:xik表示第i个数据向量的第k个分量;d表示数据的特征维数。

distM(xi,xj)的值越小,则xi与xj之间相似性越高。

曼哈顿距离应用在早期的计算机图形学中,将其用于衡量数据间的相似性则未必合适。图6给出了在二维情况下,使用曼哈顿距离表征数据间相似性的示意图。可以看出,相同相似度区域呈现菱形分布的特点,但这种分布使得与中心原点距离相同的2个数据点(图中的2个黑点)却与中心点具有不同的相似性。

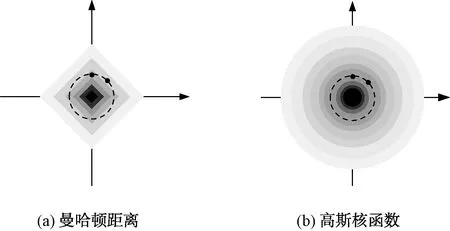
图6 基于曼哈顿距离和高斯核函数的数据相似性

针对曼哈顿距离不能很好地度量数据间相似性的不足,将高斯核函数用于数据相似性度量,使用式(10)代替1/(dist(·)+ε)进行相似性度量:

(10)

式中:参数σ用于控制高斯核函数的径向作用范围,一般取所有数据距离的平均值即可;sG(xi,xj)值越大,则xi与xj之间相似性越高。

高斯核函数具有更大的作用范围,并且能够实现数据的非线性映射,将原始低维特征xi和xj映射到具有无限高维的φ(xi)和φ(xj)。这种高维映射的特性,使得原本在原始低维空间不可分的数据能够在高维空间中线性可分,因此高斯核函数比曼哈顿距离更适合用于衡量数据间的相似性,尤其在数据维度高或线性不可分时。图6(b)给出了二维情况下的基于高斯核函数的数据相似性示意图。

基于上述分析,表1给出了TL-FNDCReK迁移学习算法的基本流程。

表1 TL-FNDCReK迁移学习算法的基本流程

2 基于迁移学习的辐射源识别分类方法

如图7所示,本文将第1节提出的TL-FNDCReK迁移学习算法用于辐射源个体识别。

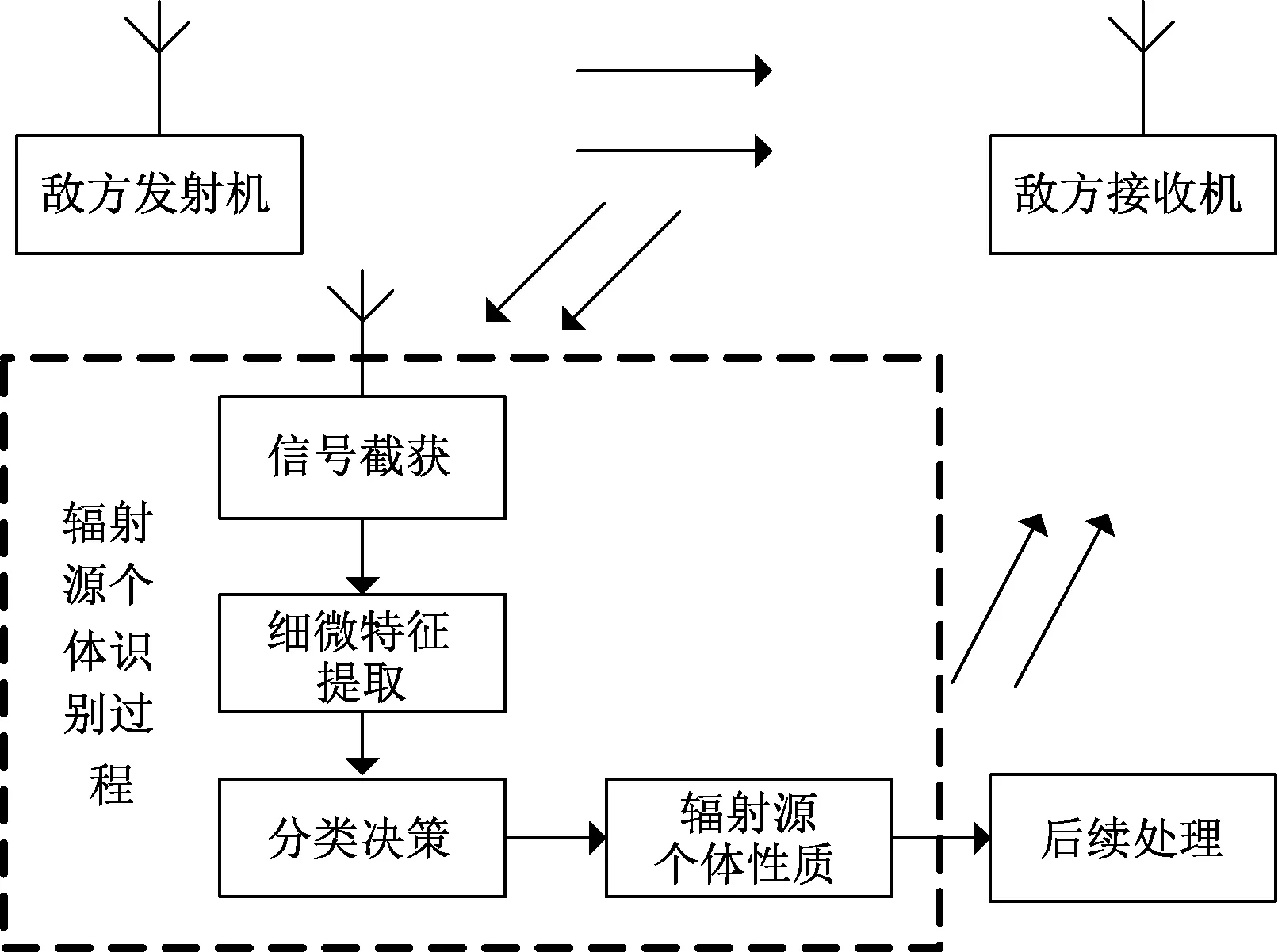
图7 辐射源个体识别框架

截获到敌方辐射源的信号后,接下来的任务是提取能够表征辐射源细微特征的特征参数。经过提取大量辐射源细微特征进行对比,最终本文选取了包括非线性、非平稳和非高斯特征在内的3大类、6小类特征,具体为:包络盒维数[9]、信息维数[9]、Lempel-Ziv复杂度[9]、高阶R特征[10]、高阶J特征[11]、Hilbert时频能量参数[12]。图8举例给出了对某电台辐射源数据所提取的特征。

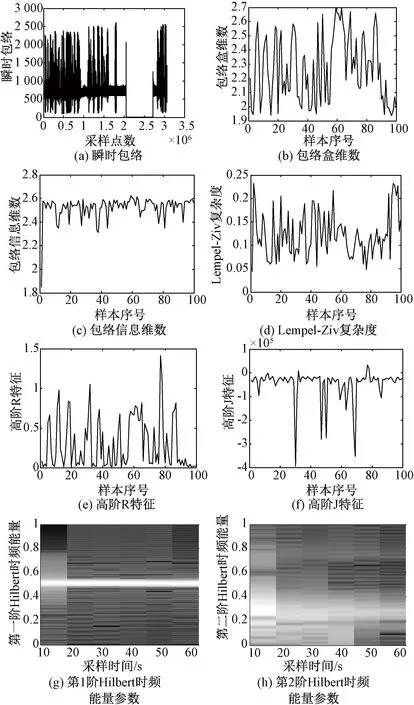
图8 电台辐射源信号特征

如何利用提取的信号特征对辐射源个体进行有效识别是分类决策要解决的问题。在现实中,辐射源个体特征受时间、空间、应用条件等因素的影响,不同时间段某一辐射源设备具体组网方式、使用情况都不相同,不同时间段获取的数据往往并不完全服从相同分布。然而,传统机器学习的前提假设是数据始终符合相同分布,否则就难以达到可靠的分类识别效果。迁移学习不需要传统机器学习的这种假设,能够从与目标域不同但相似的源域数据中挖掘有用知识并迁移到目标域学习中。在分类决策阶段使用迁移学习训练分类模型,将有助于提高对辐射源个体识别的性能。为此,将本文第1节提出的TL-FNDCReK迁移学习算法用于辐射源个体识别的分类决策,提出了一种基于迁移学习的辐射源个体识别分类方法。在分类决策阶段,基于迁移学习分类决策的数据处理流程如图9所示。

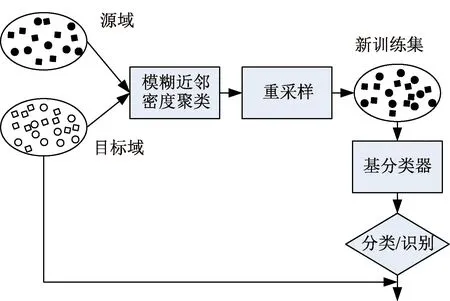
图9 基于TL-FNDCReK的数据处理流程图

3 实验结果分析

本文实验采用的数据为外场实测电台辐射源数据。

3.1 实验数据

采集了2部不同工作频率、不同说话人、不同传播环境的同类型调频电台实测数据。电台型号、批次相同,工作频率为160 MHz和410 MHz。采用3个不同说话人形成基带话音调制,分别在近距离有直达波和远距离无直达波的传播环境进行接收,接收机信道带宽为100 kHz,发射信号带宽为25 kHz,以204.8 kHz的采样频率进行采样。采集到辐射源信号后,提取第2节所述的信号特征用作后续的分类决策。

3.2 实验结果

在迁移学习实验设置中,将160 MHz工作频率的1号说话人远距离无直达波电台话音数据集作为目标域,并从每类数据中随机选择100个样本作为目标域测试数据。源域则选择与目标域不同的数据集:410 MHz工作频率的1号说话人远距离无直达波数据(Source 1)、160 MHz工作频率的2号说话人远距离无直达波数据(Source 2)、160 MHz工作频率的3号说话人远距离无直达波数据(Source 3)或160 MHz工作频率的1号说话人近距离有直达波数据(Source 4)。选定源域数据集,再从每类随机选择NS=r′×100个数据作为源域数据,其中r′为源域训练样本数与目标域测试样本数的比值,实验中r′的取值范围为[0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]。为了验证所提算法对采用不同基分类器均有较好的性能提升,分别使用2种基分类器进行实验:C4.5决策树和朴素贝叶斯(Naïve Bayes)。为简化表述,将基于线性模糊近邻归属度和基于指数模糊近邻归属度的TL-FNDCReK算法分别用TL-Linear、TL-Exp表示。

将所提算法的2种类型TL-Linear、TL-Exp与Baseline和BRSD算法进行对比实验。其中,Baseline表示直接使用源域数据作为训练集训练基分类器,然后对目标域数据进行分类识别,不存在迁移学习过程。表2～表5分别给出了选择不同源域数据时,20次重复独立实验的识别准确率平均结果。不同方法间的识别率最大值用加粗字体表示。每个表格的最后一行给出了每一方法对训练样本个数的识别率平均值。

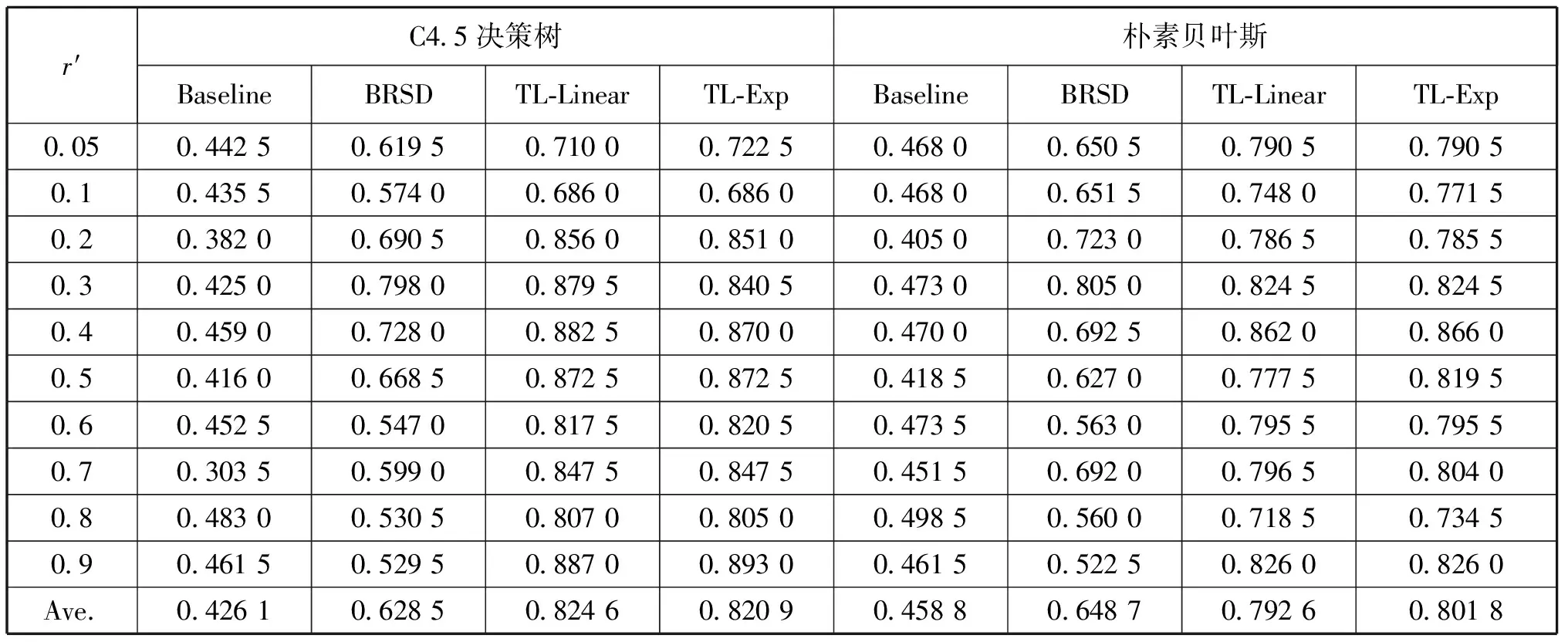
表2 源域数据采用Source 1数据集的分类识别率

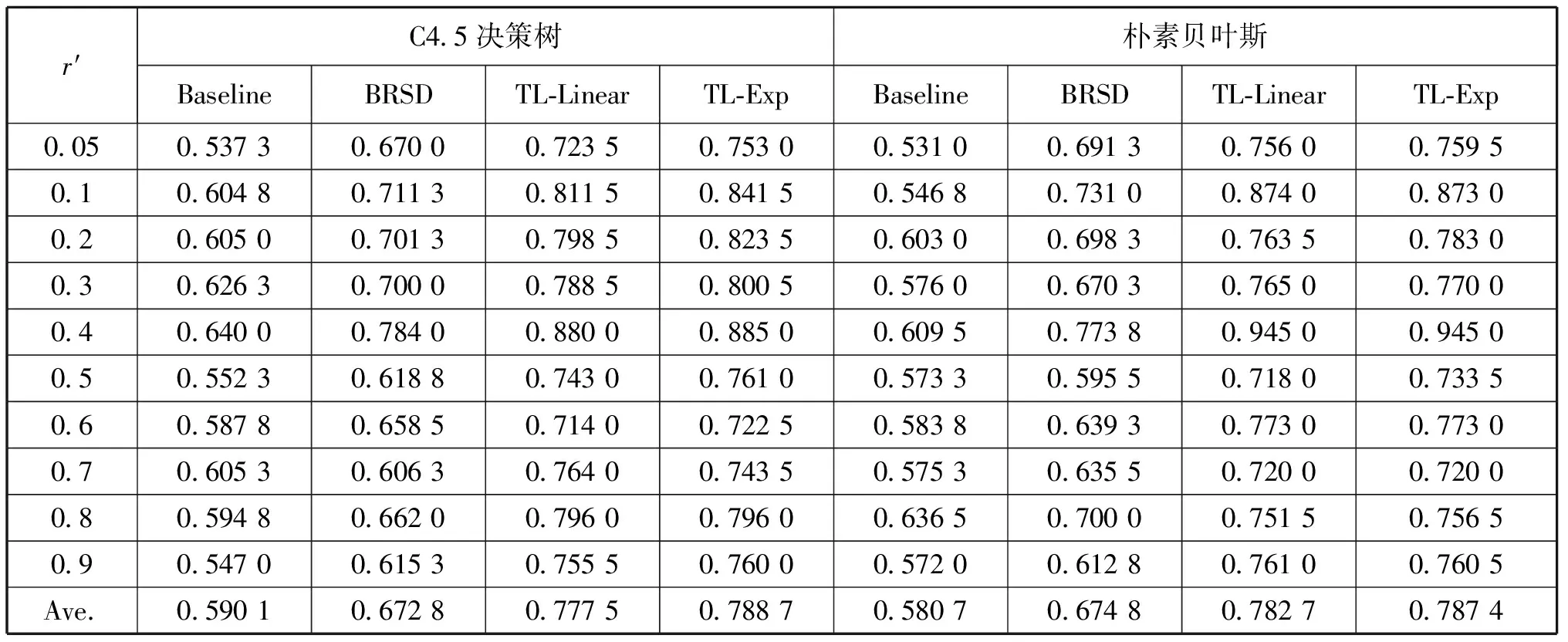
表3 源域数据采用Source 2数据集的分类识别率

表4 源域数据采用Source 3数据集的分类识别率

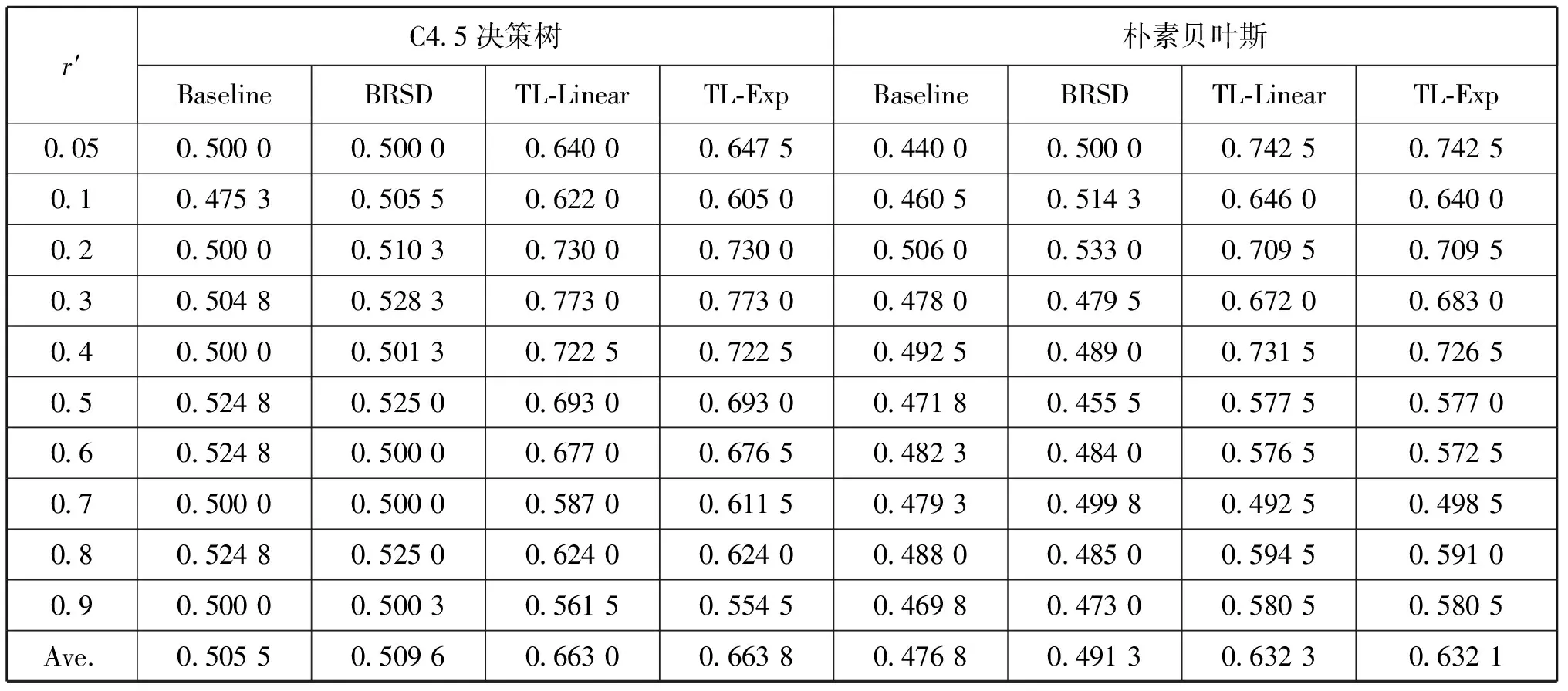
表5 源域数据采用Source 4数据集的分类识别率

通过表2～表5可以看出,TL-FNDCReK(TL-Linear和TL-Exp)在大部分情况下都能够有效地提高识别率,这主要归功于其能更好地挖掘数据结构信息。Baseline直接使用源域数据而没有考虑域间差别,其识别率大多数情况都很低。基于频率变化、说话人变化(Source1、2、3)的识别率要高于传播环境变化(Source4)的识别率,这可能是因为近距离有直达波的信号特征与远距离无直达波的信号特征差别较大、可用于迁移的共同知识较少造成的。通过比较还可以发现,在TL-FNDCReK 2种类型中,TL-Exp的识别效果要略优于TL-Linear。总之,相比于Baseline和BRSD,TL-FNDCReK能够取得更高的识别率,较好地完成了SEI任务。

图10给出了训练样本不同个数时的平均识别率,可以看出,所有方法的识别率并不随着源域样本个数的增加而单调提高,甚至会有所下降。这种现象的一个可能解释是:由于域间差异,从源域能够迁移到目标域的有用信息是有限的。当源域数据达到一定数量时,源域就无法提供更多的有用信息,相反还会对目标域的学习造成干扰。

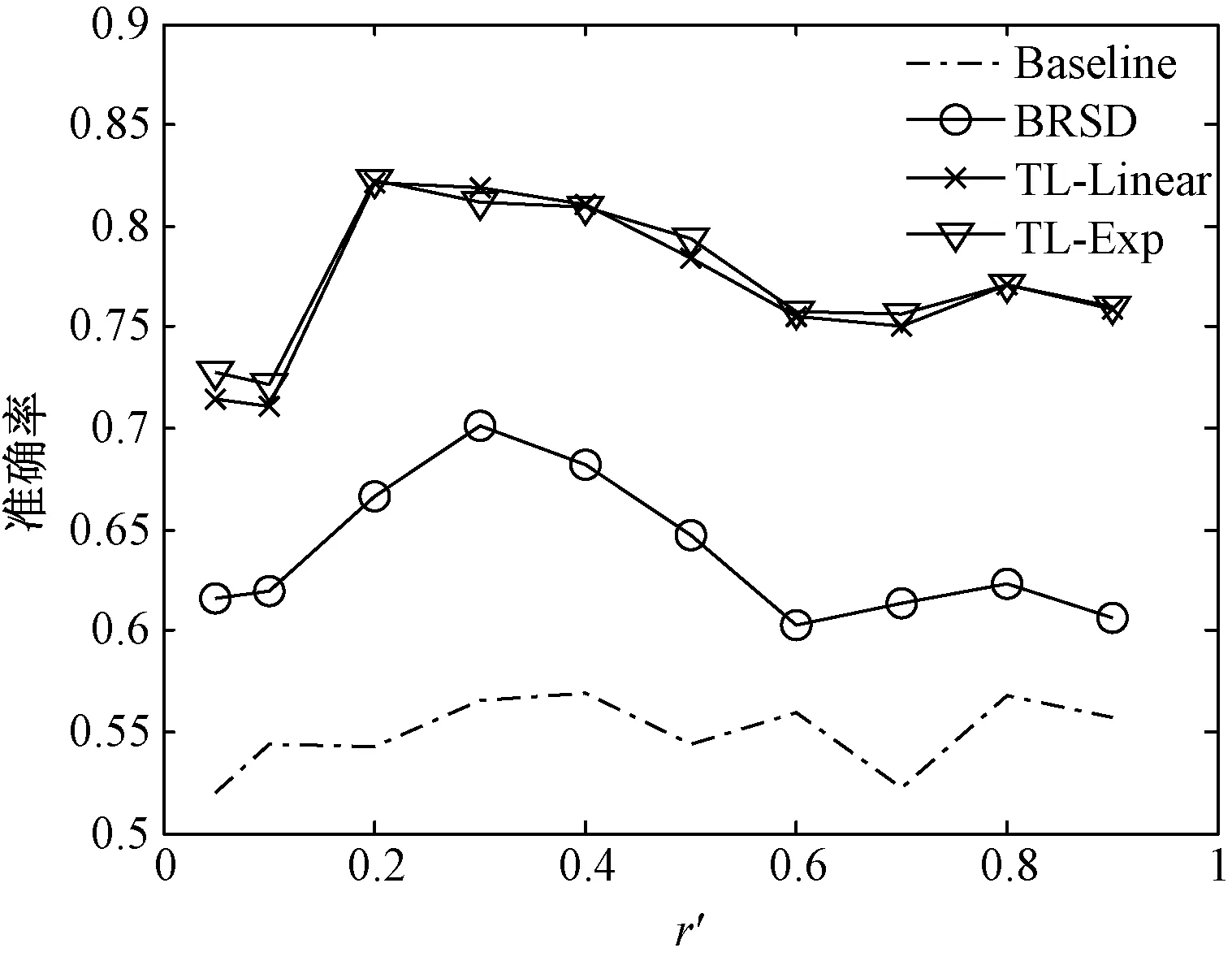
图10 不同训练样本比例的平均识别率

3.3 参数选择

在TL-FNDCReK的聚类分析过程中,模糊近邻归属度的主要参数为m0,下面实验分析m0对算法的影响。图11给出了源域数据为410 MHz工作频率的1号说话人远距离无直达波数据,r′=0.2,基分类器为朴素贝叶斯分类器,m0分别取10-10、10-6、10-5、10-4、10-3、10-2、0.1、0.5、1的识别准确率。

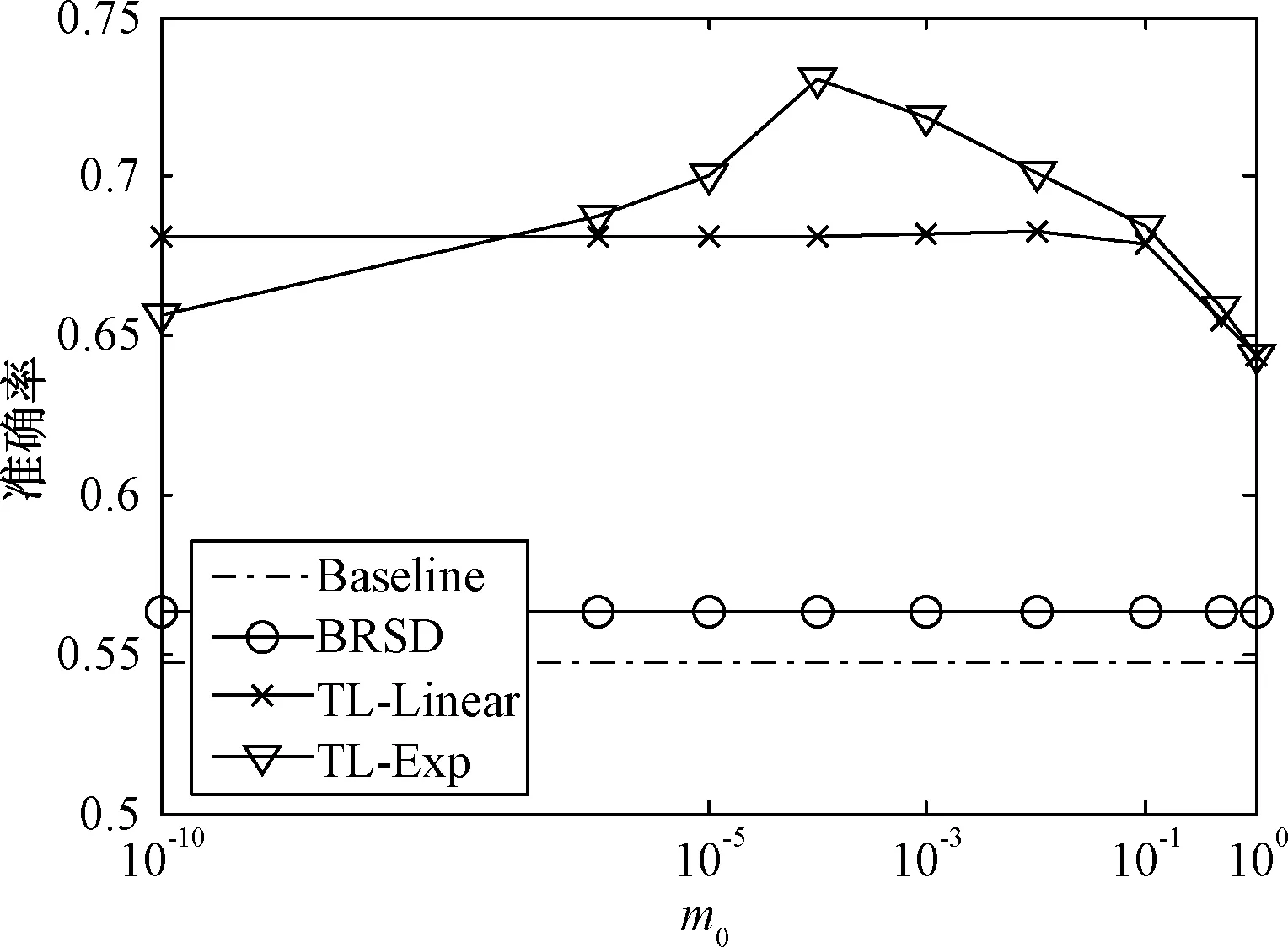
图11 参数m0对算法的影响

由于Baseline和BRSD使用的离散近邻归属不存在参数m0,其识别率与m0无关。当m0趋于0时,TL-Linear的识别率趋于稳定,而TL-Exp却一直在变化。这种差别是由它们的模糊近邻归属度的性质不同决定的。如图12(a)所示,在m0趋于0时,线性模糊近邻归属度也都趋于相同,因而TL-Linear的识别率能够趋于稳定。而不论m0如何趋近于0时,指数模糊近邻归属度都有明显的区别,如图12(b)所示。当m0取非常小的正数时(如m0=10-10),处在r邻域内相当大区域里的数据的指数模糊近邻归属度都近似为0,即m0取值过小不仅改变了指数模糊近邻归属度的性质,而且使实际起作用的r值变小。因此,在TL-Linear中,m0一般取0值即可;在TL-Exp中,同时考虑m0对近邻归属度和r的影响,m0的取值一般不能太小,通常取[10-3,10-1]范围内即可。

图12 m0对模糊近邻归属度的影响

4 结束语

立足于辐射源个体识别应用的特点,本文提出了一种基于迁移学习的辐射源个体识别分类方法。该方法通过聚类分析和重采样从数据集中选择新训练样本用于目标域学习,使用模糊近邻密度聚类提高对参数选择的鲁棒性及不同分布数据的适应性,并使用高斯核函数度量数据间的相似性以提高新训练样本选择的可靠性。通过实测数据实验,验证了该算法的性能。此外,在实验结果的基础上,通过理论分析,对源域样本个数对识别性能的影响进行了分析,并指出了模糊近邻归属度的重要参数m0的选取范围。目前,TL-FNDCReK方法仍有进一步研究的方向,如更加有效地估计参数r,更有效的重采样策略等。