基于数据重构的杂波抑制方法

马艳艳,洪 伟,齐永梅

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引 言

雷达作为战场上的“眼睛”,自20世纪在战场上应用以来,成为各个国家重点研究的对象,在现代战争中占据非常重要的地位。随着侦察、电子对抗等技术的发展,雷达的工作环境越来越复杂,要实现雷达对危险目标的跟踪,首先要降低虚警概率和漏警概率,解决杂波、干扰等因素对目标检测的影响[1]。杂波有多种类型,分为地物等静止杂波和云雨等运动杂波。当杂波不运动时,若雷达在运动平台上,雷达接收到的杂波也是有一定速度的。

目前比较成熟的杂波抑制方法有动目标指示(MTI)、动目标检测(MTD)、杂波图检测技术[1]。MTI技术对固定杂波的抑制效果很好,但像海杂波这种有一定频谱宽度的杂波,经过对消处理后,依然会有杂波残留[2]。

基于MTI发展的MTD技术,通过快速傅里叶变换(FFT)滤波器组可以抑制有一定谱宽的杂波,可以通过自适应扣通道技术去除有一定速度的目标,但当杂波的中心频率和目标相近时,往往会造成目标的丢失。

杂波图检测技术自20世纪90年代发展以来,日趋成熟,已经广泛在装备上使用,并通过多种试验,但杂波图检测技术需要存储多个雷达天线周期的数据,对存储能力和计算能力有较高的要求。

目前,大量关于重构算法的研究应用到雷达上[3]。文献[4]提出了使用稳健字典学习的方法重构雷达高分辨距离像,通过试验验证了重构后的雷达高分辨距离像(HRRP)识别率效果更好。文献[5]提出了一种基于经验模态分解(EMD)-CLEAN算法的飞机目标识别方法,数据经过变换后,重构特征,完成特征提取的功能。文献[6]针对微弱目标图像的检测难题,提出了基于稀疏表示的杂波抑制方法,通过计算超完备字典的系数和原子向量对图像进行重构,可以实现杂波的自适应抑制,进而提高信杂比,提高检测性能。文献[7]提出了一种基于概率主成分分析的重构方法用于人和车辆的分类,通过概率主成分分析模型对雷达回波进行建模,然后使用贝叶斯信息(BIC)准则自适应选择噪声门限,基于实测数据进行的对比试验表明,所提重构算法在信噪比为15 dB时较重构前的算法其识别率提高了15个百分点。文献[8]针对海面目标提出了多种稀疏算法。首先对数据进行重构,然后进行目标检测,实验结果表明,重构后的数据提高了目标的检测概率。文献[9]针对传统方法中抑制干扰分量时卫星导航信号损失的问题,提出了基于奇异值分解的抗干扰方法,通过实验验证了新方法可以在剔除干扰的同时有效保留卫星导航信号,提升了抗干扰能力。

通过以上文献梳理,本文提出一种基于奇异值分解的数据重构方法,利用特征值对应谐波能量的理论,抑制掉杂波对应的特征值,保留信号的特征值,实现杂波抑制的功能,基于实测数据进行的与常规信号处理方法对比的实验表明了所提杂波抑制方法的有效性。

1 基于奇异值分解的数据重构

将雷达反射回波表示为信号、杂波及噪声叠加的形式:

x(t)=c(t)+s(t)+w(t)

(1)

式中:t代表某次采样时刻;c(t)表示杂波;s(t)表示信号;w(t)～CN(0,σ2)代表接收到的噪声。

对雷达回波数据进行奇异值分解:

(2)

式中:N表示窗长;xi为第i次滑窗得到的数据;X表示1个相参处理间隔的采样数据经过滑窗得到的矩阵。

那么奇异值分解表示为:

X=UΣVT

(3)

式中:U=[U1U2…UN];V=[V1V2…VN],为特征向量矩阵;Σ=diag{λ1λ2…λN},为特征值对角矩阵。

首先,对特征值矩阵的特征值从大到小排列,即:

(4)

经过门限判决后,特征值对应的对角矩阵需满足以下条件:

(5)

式中:Th为杂波门限。

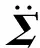
于是将去杂波后的信号表示为:

(6)

数据重构算法进行杂波抑制的基本思路是,当目标能量大于杂波时,把奇异值分解的特征值按照从大到小的顺序排列,结合杂波特性通过实验选择1个合适的门限。当特征值大于该门限时,认为特征值对应的分量是由目标产生的,该特征值保留;当特征值小于该门限时,认为对应的特征值是由杂波产生的,将其置为零。利用新的特征值矩阵和特征向量矩阵重构雷达时域回波信号,则重构后的信号即为去除杂波的时域信号。

2 实验验证

2.1 数据介绍及处理流程

本文实验所用数据为某型雷达在海面工作时录取的实测数据,雷达发射线性调频信号,相参积累点数为16,目标2个,本文实验数据为基带数据做过舰速补偿和脉压处理后得到的数据,录取的数据为高信噪比的,故本文不考虑噪声的影响,只验证杂波抑制性能。

数据处理流程如图1所示,由4个步骤实现。

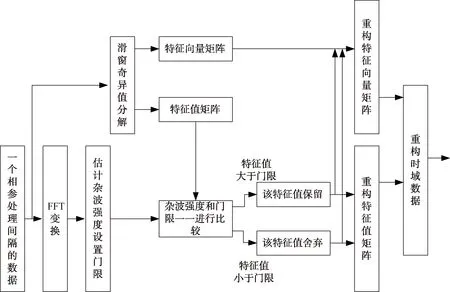
图1 数据处理流程

第1步,对一个相参处理间隔的数据做快速傅里叶变换,根据指令字选择要扣除的通道,用于估计杂波的强度φ,设置相应的系数k来确定杂波门限kφ,本文根据实验效果取k值为1/8;

第2步,对一个相参处理间隔的数据滑窗得到矩阵,对矩阵做奇异值分解,得到特征值矩阵和特征向量矩阵;

第3步,将门限和特征值进行比较,依照式(4)和式(5)准则构建新的特征值矩阵和特征向量矩阵;

第4步,利用式(6)重构时域数据,对重构后的数据进行传统的MTD和恒虚警率(CFAR)处理后,得到视频数据。

2.2 试验结果

图2所示横坐标表示16个多普勒通道。图2(a)目标在第8个通道,第2～4个通道为杂波;图2(b)目标在第6个通道,第1～3个通道为杂波。从图2重构前和重构后的对比图可以看出,当目标和杂波的最大幅值相近时,重构方法依然可以抑制杂波,只是目标的频谱有所展宽,能量有所损失。

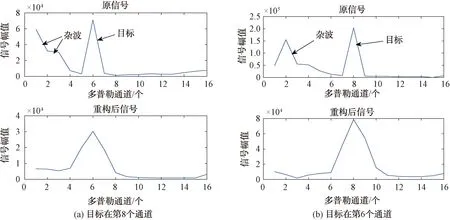
图2 目标和杂波幅值相近时重构前后杂波抑制效果图

图3(a)所示为目标在第11个通道,第2个通道为录取数据中的杂波,第6个通道为人工加入的能量比目标低的杂波。从重构前后的对比图可以看出,当目标和杂波的能量差异较大时,重构方法可以在抑制杂波的同时有效保留目标信息。图3(b)所示为只包含杂波无目标的情况,第1～3个通道为杂波,由对比图可知,杂波可以被很好地剔除掉。

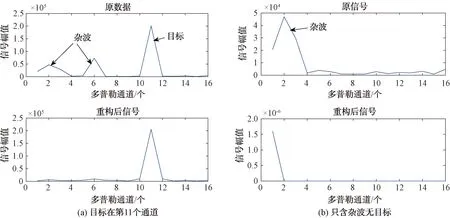
图3 目标和杂波幅值相差较大时重构前后杂波抑制效果图

图4(a)所示为基带数据经过常规信号处理(MTD、CFAR算法处理)之后的视频图,图4(b)为时域数据先经过本文所提方法进行初步杂波抑制之后,再采用常规信号处理(MTD、CFAR)算法的视频图。2种方法都可以将2个目标检测出来,但图4(b)比图4(a)的杂波少了很多,对比结果证明了本文所提杂波抑制方法的有效性。

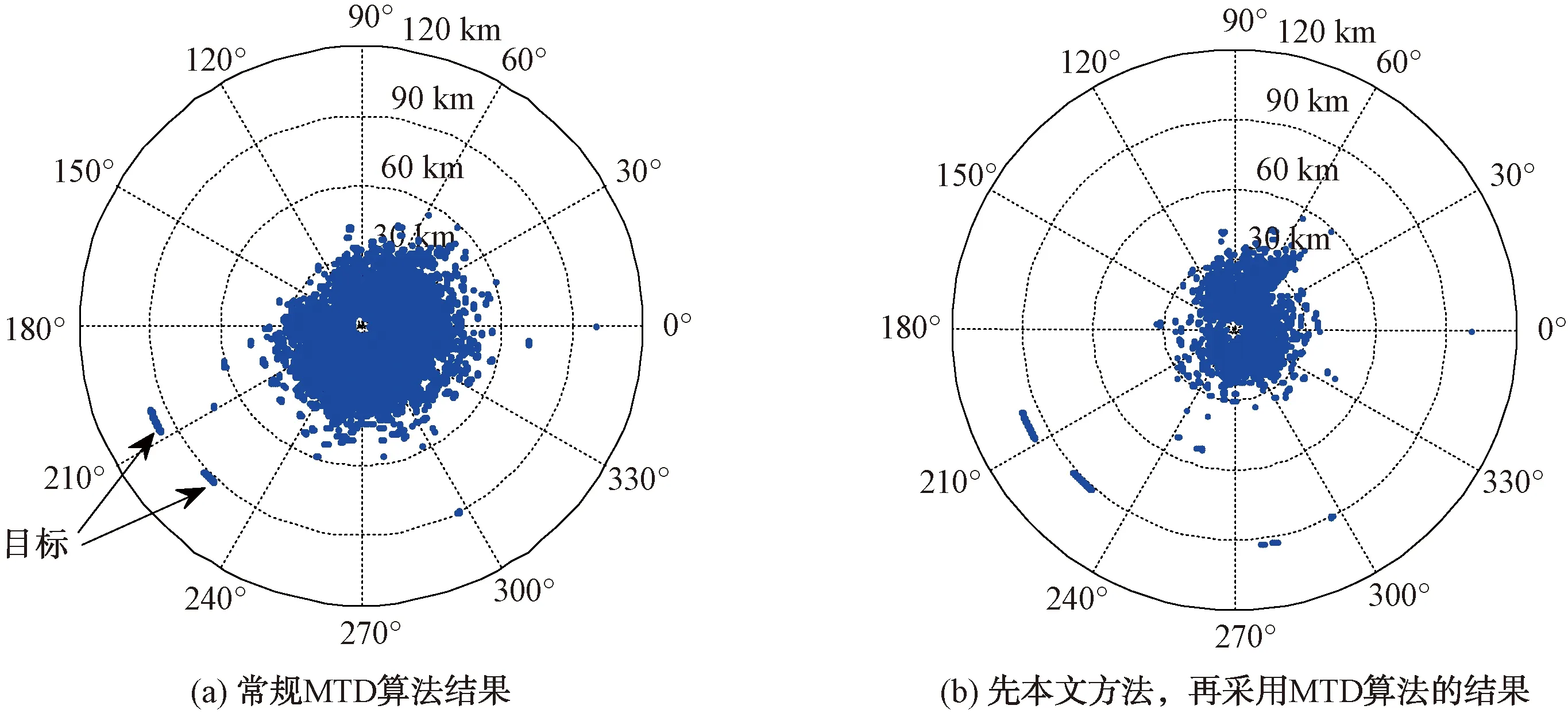
图4 对比效果图

3 结束语

目前成熟的MTD技术在进行杂波抑制时,根据指令进行不同通道的扣除,当杂波频率和目标频率相近时,扣除部分多普勒通道的处理方法可能导致目标损失较大或杂波抑制效果不理想。本文针对该问题,提出一种基于数据重构的杂波抑制方法,对重构后的时域数据再采用常规的MTD和CFAR处理方法。基于实测数据进行的对比实验表明,采用本文所提方法处理后得到的视频数据,杂波得到了较好的抑制。