孔隙率对五元陶瓷体系材料热导率的影响
2023-04-19陈宇慧姜鹏洋张若琳孙家祥张百强张永海
陈宇慧,姜鹏洋,张若琳,孙家祥,张百强,张永海
(郑州轻工业大学 能源与动力工程学院,郑州 450000)
在高温推进和能源发电系统中,复杂的热化学和热机械环境通常要求使用不同性能的材料组合。材料的组合能够同时优化机械、热性能和耐腐蚀性能,从而实现设计和系统性能的突破[1]。航空航天领域常用热障涂层对热端部件进行防护,目前应用最广泛的陶瓷层材料是YSZ(yttria-stabilized zirconia,YSZ)。随着航空航天技术的发展,对推重比的要求越来越高,发动机燃烧室的温度也随之提高,未来发动机燃气温度极有可能超过2000 ℃,而材料表面温度也会超过1500 ℃,因此对热端部件的防护材料也提出了更高的要求[2-3]。YSZ 在超过1200 ℃时不仅会发生相变,随着使用时间的延长,材料晶粒也会发生烧结导致涂层的致密度提高,孔隙率降低,热导率增大,不能有效地对热端部件实行防护[4-6]。因此开发耐高温,低热导的新型隔热陶瓷材料迫在眉睫。新型隔热陶瓷材料需要具备以下特点:(1)材料本身具有低的热导率;(2)热力学稳定;(3)能产生具有一定比例且结构稳定的孔隙[7]。
热导率是热障涂层材料重要的热物性参数之一。稀土氧化物掺杂制备低热导率热障涂层是目前主要研究趋势之一。Zhao 等[8]通过实验测得致密的8YSZ 在1000 ℃下的热导率为2.3 W·m-1·K-1;Wang 等[9]研究表明ZrO2掺杂CeO2、Nd2O3等材料可以降低材料的热导率,提高相稳定性,但抗高温烧结性能的改善不明显。在此基础上,学者们[10-13]分别通过Al2O3、CeO2、Gd2O3、Sc2O3等多种稀土氧化物共掺杂ZrO2代替Y2O3的单一掺杂,形成了具有多点位错、晶格缺陷、互补效应的新型陶瓷材料,可有效抑制相变,提高热稳定性,降低热导率,同时提高材料的结合强度、耐磨性和断裂韧性。对于锆酸镧(La2ZrO7)材料同样有研究人员研究其掺杂性能,如Shen 等[14-16]分别研究了Ce4+、Gd3+和Sm3+对La2ZrO7涂层性能的影响,发现掺杂会导致La2ZrO7涂层的晶格常数发生变化,晶体结构发生畸变,并使晶体相更加稳定,使La2ZrO7涂层结构发生更好的变化,从而获得更低的热导率、与基底更加匹配的热膨胀系数、更好的热冲击寿命和热循环寿命。以上研究发现,掺杂离子与Zr4+半径的差异越大,则会形成更多的氧空位和高浓度的晶格缺陷,致使声子散射增强,材料的热导率降低。近年来,由五种或五种以上氧化物组成的高熵陶瓷(high entropy ceramics,HEC)受到越来越多的关注,高熵陶瓷具有低热导率、良好的高温稳定性、慢扩散速率和严重的晶格畸变等特性,其特点是金属元素在阳离子位置存在固有的原子无序,导致成分复杂,晶格畸变显著[17]。目前的低热导陶瓷材料除YSZ,只有ZYTO 体系具有相变增韧和铁弹增韧的特性,但其稳定相区狭窄、Ta 易偏析很难实际应用。本工作则是在ZYTO 体系的基础上引入Ti4+替换部分Zr4+,Er3+替换部分Y3+制备出高熵陶瓷,通过对比(ZrYTaErTi)O 陶瓷在不同配比下的热物理性能,对该体系陶瓷进行筛选,以寻得具有低热导、高温相稳定的陶瓷材料。分子动力学(molecular dynamics,MD)模拟作为一种有效的材料微观分析手段,在材料的热物性研究方面取得了较大的进展,为研究材料的热物理性质提供强有力的手段。目前分子动力学模拟低热导率研究最广泛的掺杂材料是6~8YSZ[18]、烧绿石结构的La2Zr2O7和Gd2Zr2O7(GZ)[19-20]等,这些材料热导率低的原因是具有高浓度的点缺陷,如取代原子所产生的氧空位等。Schelling 等[21]通过MD 模拟计算了YSZ 的热导率,并与实验数据进行比较,发现其模拟是可行的。在此基础上,Wang 等[22]通过MD 模拟ScYSZ材料的导热系数,来探究掺杂元素对YSZ 热导率的影响,发现掺杂Sc3+元素可以降低YSZ 的热导率。此外赵梦甜等[23]研究了纳米孔对YSZ 材料热导率的影响,发现孔隙的存在可以增强声子散射并进一步降低块体YSZ 的热导率。
本工作研究200 ℃到1200 ℃内(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O(x=0.2、0.544、0.672、0.796和0.92)陶瓷材料样品的热导率。用氧离子在系统中的均方位移(mean square displacement,MSD)描述氧离子在陶瓷样品内的振动强度来反应热导率的变化。研究不同孔隙率与元素含量对(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 热导率的影响。
1 实验方法及模拟
1.1 实验方法
选取ZrO2(99.99%)、Y2O3(99.99%)、Ta2O5(99.99%)、Er2O3(99.99%)和TiO2(99%)粉末作为原料。通过固相反应法制备(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O(x=0.2,0.544,0.672,0.796和0.92)复合材料,配比如表1。

表1 材料组成(摩尔分数/%)Table 1 Composition of material(mole fraction/%)
首先将粉末与丙醇混合,并在球磨机中研磨10 h,然后在120 ℃下干燥12 h。将测量热导率的样品在220 MPa 下压制成粒料,置于高温炉中1600 ℃下烧结20 h,然后将烧结的粒料加工成所需的尺寸(ϕ12.7 mm×1 mm)。在1500 ℃下进行热蚀刻2 h 以测量烧结样品的晶粒尺寸。通过JEMARM200F 型扫描电子显微镜观察材料的微观结构,观察前需将陶瓷样品材料的测试面进行喷金处理。
使用LFA427 型激光闪光仪测量样品的热扩散率,测量范围为20~1100 ℃,间隔为100 ℃。在热扩散率测试之前,在样品的前后表面沉积一层石墨薄膜,用于热吸收激光脉冲。每个样本在相应的温度下测量三次,每100 °C 记录一次数据。利用阿基米德排水法测定样品的密度。导热系数由式(1)获得:
式中:λ为导热系数;α为样品的热扩散率;ρ为样品的密度;Cp为比热。
复杂化合物的比热Cp在初始100~500 ℃时是由差示扫描量热仪测得,随后600~1000 ℃的温度则是根据Neumann-Kopp 定律,通过拟合计算得到的,拟合公式如式(2)所示:
式中:a、b和c均为拟合常量。
固相合成法制备的陶瓷试样烧结后不可能是完全致密的,因此热导率的计算值需要进一步修正,修正公式如式(3)所示:
式中:ρpore是烧结样品内部的孔隙率,λ0为完全致密样品的导热系数。
1.2 模拟方法及模型
利用大型分子模拟软件包LAMMPS 模拟(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O(x=0.2、0.544、0.672、0.796 和0.92)陶瓷材料的热导率。在模拟中,用Born-Mayer-Buckingham 对势和静电相互作用来描述原子间作用力。其中,由库仑项和Ewald项组成的长程相互作用描述静电相互作用,Born-Mayer-Buckingham 对势用来描述短程相互作用[24-25],对势函数的具体描述如式(4)所示:
式中:rij是第i个离子与第j个离子的相互作用距离;qi、qj是第i个离子与第j个有效离子的电荷,对于O2-、Zr4+、Y3+、Ta5+、Ti4+和Er3+分别为-2、+4、+3,+5 和+3;Eij表示体系的总能量,其他参数如Aij、Bij和Cij从文献[26-27]中获得并列于表2。

表2 原子间的势参数Table 2 Parameters for the interatomic potentials
用Material Studio8.0 构建了6×6×50 的t-ZrO2单胞,如图1 所示。Y3+、Ta5+、Ti4+和Er3+离子在构建模拟模型时随机取代Zr4+离子,并产生相应数量的氧空位以维持电中性。在模拟过程中,原子的初始速率是从给定温度下的Maxwell-Boltzmann distribution 中随机选取的。该系统采用Langevin方法对温度和体积进行控制。时间步长设为0.0001 fs,牛顿运动方程采用Velocity-Verlet 算法求解。以热导率的计算为例,所谓的“初始弛豫”计算分别在NVT 和NVE 系综下各进行200000 步(200 ps)以获得平衡系统,平衡模拟单元在模拟温度T(200、400、600、800、1000 ℃和1200 ℃)下进行600000 步达到平衡状态,然后收集热力学信息进行热导率的计算。

图1 物理模型Fig.1 Physical models
傅里叶定律计算导热系数,可用式(5)描述:
式中:λ为导热系数;J为热流;为温度梯度;A为传热面积。
图2 给出了热传导模型,其中中间层被定义为换热区域,左端是热板,右端是冷板。换热区域垂直于超级单体的Z轴。一般来说,固体材料的导热系数取决于自由电子、声子和光子。根据动力学理论,可得出对于(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O陶瓷材料,其内部热输运是由声子载能的定向运动决定[28]。

图2 热通量示意图Fig.2 Illustration of heat flux
2 结果与讨论
2.1 样品表征
烧结样品的晶粒尺寸是影响材料相结构和热物理性能重要参数之一,因此,对五种样品进行了SEM 表征,热蚀刻后的烧结样品的SEM 形貌如图3 所示。通过Image J 软件对五种样品的孔隙率进行计算,发现所有样品的孔隙率均低于5 %,致密度较高,所有样品的晶粒尺寸均大于0.8 μm。

图3 S1~S5 的SEM 图(a)S1;(b)S2;(c)S3;(d)S4;(e)S5Fig.3 SEM morphologies of S1-S5(a)S1;(b)S2;(c)S3;(d)S4;(e)S5
材料参数见表3。文献[29]研究表明,热导率对晶粒尺寸存在依赖性。其原因是晶界对声子平均自由程谱的限制。对于较小的晶粒,平均自由程大于晶粒尺寸的声子更容易散射,从而降低传导热能的能力。

表3 材料S1~S5 的参数Table 3 Parameters of S1-S5
2.2 热导率
S1~S5 块体材料热导率如图4 所示,其中,S5 样品的热导率最高,均出现在900 ℃条件下(实验热导率约为4.889 W·m-1·K-1,模拟热导率约为6.567 W·m-1·K-1)。对比发现,通过模拟得到的热导率数值要大于实验的结果。造成这种结果的其中一个原因是多元陶瓷体系实验样品中含有大量的点缺陷、裂纹、晶界和气孔等。模拟结果与实验结果相比,模拟结果比实验结果大的原因是MD 模拟中理论模型只考虑了氧空位,没有加入点缺陷、裂纹、晶界和气孔等缺陷,导致模型相较于实际样品更加致密,没有晶界散射,使声子散射中心变少,因而热导率较模拟值更低。声子的平均自由程较实验值越大,则热导率比实验值也越大。声子的平均自由程可用式(6)描述为[28]:
式中:li(ω,T)为 声子-声子的平均自由程;lp(ω)为点缺陷散射所减少的平均自由程;lb为晶界散射所减少的平均自由程。
根据式(6)可知,点缺陷、晶界和位错等缺陷的存在导致声子的数量增加,提高了声子碰撞的概率,进一步增强了声子的散射,改变了声子的初始传热方向并释放其能量。同时碰撞引起能量损失,声子的传输发生减弱或终止,导致(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 陶瓷样品声子的平均自由程减小,热导率降低,声子散射与热导率成反比。S5 的热导率最大,是因为S5 掺杂氧化物的量在几组样品中最少,具有更少的氧空位,使得S5 的声子散射较其他组弱,声子的平均自由程大。由于原子间距较窄,较小的晶格参数可能会阻碍声子传输,热导率的模拟结果比实验结果要大得多[30]。模型尺寸(约10~20 nm)比实际样品的尺寸小得多。计算模型的尺寸限制也导致热导率相差较大[8,31-32]。
从图4(b)可以看出,S5 的测量值相较于其他几组,增加的幅度较大,这是由于实验热导率是通过样品的热扩散率、比热与密度的乘积计算获得。其中S1~S5 的热扩散率变化不大,而S5 样品的比热在400 ℃以后出现剧增。结合图3 可以看出,造成这种变化的原因是S5 试样内部存在较多的裂纹和孔隙有关。

图4 (ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 材料的热导率(a)模拟结果;(b)实验结果Fig.4 Thermal conductivities of(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O materials(a)simulation results;(b)experimental results
除缺陷外,声子数量与温度也有关系。通常情况下,声子数与温度成正比,声子数与温度之间的关系可用式(7)表示[33]:
式中:n为声子数;kB为 玻尔兹曼常数;T为温度。
通过对比图4(a)、(b)可以发现,在200~900 ℃的范围内,模拟与实验得到的热导率的趋势基本相同,都是从200 ℃开始随着温度的增加热导率升高,且均在900 ℃下达到峰值,因此模拟研究是可行的。根据公式(7)可知,在低温条件下,随着温度的增加,声子数量逐渐增多,改善了声子之间的散射强度,随着温度的增加声子的平均自由程也在增加,使声子传热的能力增强,热导率随着温度的增加而增加,而在温度升高到一定值时,声子的平均自由程会达到极值,热导率趋于平缓。
热导率模拟结果反映出该模型声子平均自由程达到极限时的温度为900 ℃。在900 ℃以后,S1~S5 的热导率开始随着温度的升高而降低。热导率的变化曲线在900 ℃出现了一个拐点,这是由于在温度达到900 ℃后,温度的增加会使声子的平均自由程减小[34]。同时,温度的升高使得声子获得更多的能量,从而使声子与缺陷发生碰撞的几率大大增加,声子散射增强,热导率出现下降趋势。在声子的平均自由程达到最低时,热导率会降低到其极限值。这与文献[35]中所描述的,即对于一般固态晶体材料,热导率随温度的增加呈现先上升达到峰值后降低到某一极限值的趋势一致。
2.3 氧离子的均方位移
氧离子位移的平方与时间呈线性关系。用材料体系中迁移的氧离子位移来判断系统中氧离子的振动强度。(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 体系中S1~S5 试样的氧离子在900 ℃时的MSD曲线如图5 所示。可以看出(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 体系的MSD 斜率在900 ℃时的关系为:S5>S3>S1>S2>S4。结果表明:在900 ℃时,(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 体系中S5 的氧离子比其他几组样品的氧离子有更强烈的振动,传热特性更强,导热系数最大。
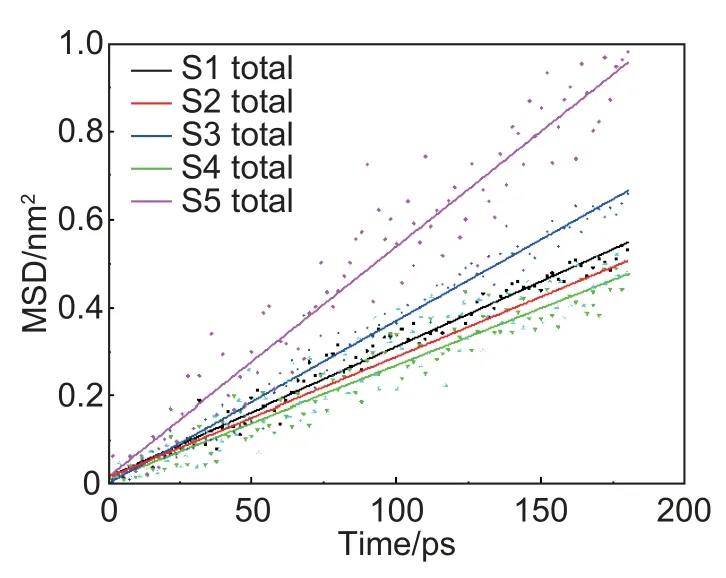
图5 900 ℃样品S1~S5 中O2-均方位移Fig.5 MSD of O2- in samples S1-S5 at 900 ℃
2.4 孔隙率
孔隙率是影响陶瓷材料热导率的重要因素之一。为了研究孔隙率对(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 体系材料热导率的影响,通过在样品模型上面开均匀的通孔,来探究其不同孔隙率下的各样品的热导率。
通过移除(ZrYTaTiEr)O 模型中选定区域内的原子来生成孔隙。孔沿模型的中心线排列,形成多孔(ZrYTaTiEr)O。模型结构如图6 所示,孔隙情况如表4 所示,所有开孔样品在相同温度下各样品热导率随温度的变化如图7 所示。由于S5 模拟的热导率结果与其他几组样品相比,受温度影响多大,因此这里不讨论孔隙率对S5 热导率的影响。
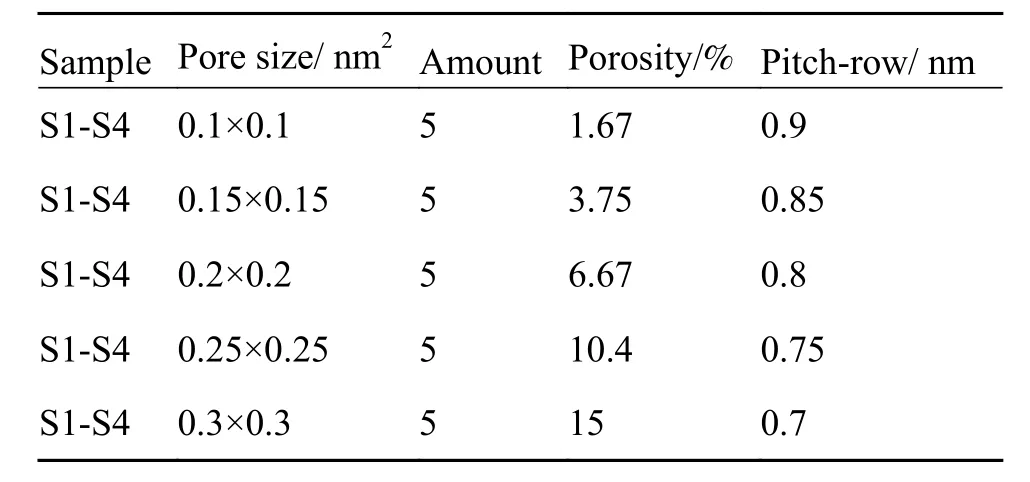
表4 (ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 多孔体系Table 4 (ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O porous system

图6 开孔后的模拟模型图Fig.6 Simulation model after opening hole
不同孔隙率下S1~S4 在200~1200 ℃的热导率变化如图7 所示,可以发现含孔隙的样品中,不同温度条件下热导率大小关系均为:S3>S1>S2>S4,这与块体样品的热导率在各温度下的大小关系一致,但含孔隙样品的热导率随温度变化趋势开始发生变化,即从200 ℃开始,样品的热导率随着温度的升高而逐渐减小。产生这样的原因由公式(5)可以看出,声子数量随温度的升高而增加,同时由于样品中孔隙的存在,同样可以增加声子的数量,并且孔隙这种缺陷可以增加声子碰撞的概率,改变声子的传播方向,释放能量后使得热导率下降。即孔隙的存在增大了其附近的声子散射,降低声子的平均自由程从而降低热导率。
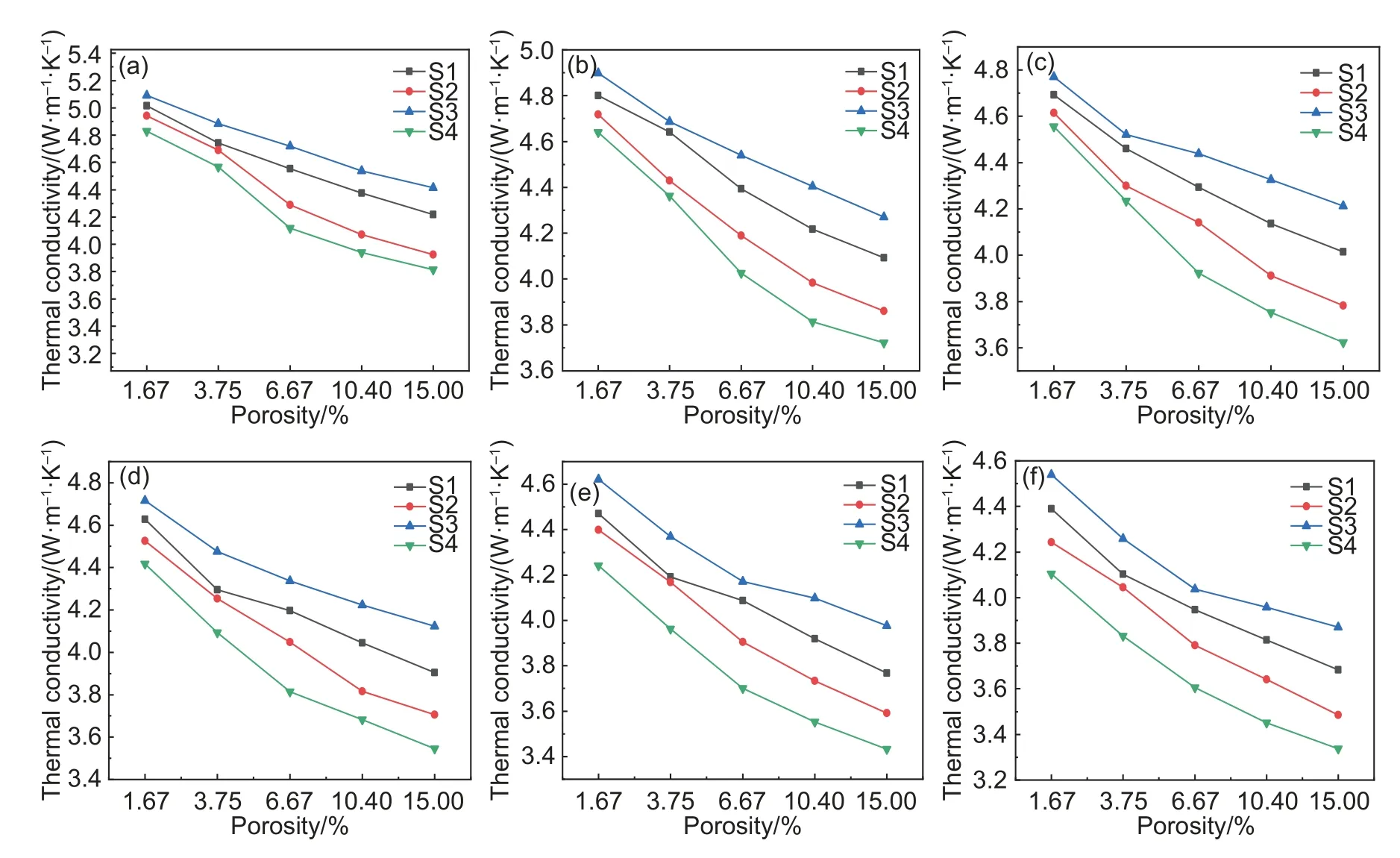
图7 不同孔隙率下S1~S4 在200~1200 ℃的热导率变化图(a)200 ℃;(b)400 ℃;(c)600 ℃;(d)800 ℃;(e)1000 ℃;(f)1200 ℃;Fig.7 Thermal conductivities of S1-S4 at 200 ℃ to 1200 ℃ with different porosities(a)200 ℃;(b)400 ℃;(c)600 ℃;(d)800 ℃;(e)1000 ℃;(f)1200 ℃;
通过对比相同温度下各样品热导率随孔隙率增加的变化趋势,可以发现,在固定温度下,随着孔隙率的增加,热导率下降,但前后下降的幅度(斜率)有所不同,即从孔隙率为1.67%开始,随着孔隙率的增加,热导率开始出现缓慢下降的趋势,在孔隙率达到6.67%后,热导率随孔隙率的增加而下降的趋势开始趋于稳定,因此可以推测在孔隙率为6.67%前后,元素组成与孔隙率对热导率的影响存在竞争关系,即在孔隙率小于6.67%时,热导率受孔隙率的影响程度不大,主要是由元素组成决定热导率,而在孔隙率大于6.67%时,主导热导率的因素转为孔隙率,因此热导率随孔隙率增大而降低。
3 结论
(1)通过比较实验和模拟的块体(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 陶瓷材料的热导率发现,(Zr0.796Y0.051Ta0.051Ti0.051Er0.051)O 的导热系数最低(900 ℃实测为1.935 W·m-1·K-1,900 ℃模拟为(6.123 W·m-1·K-1),隔热效果最好。
(2)通过比较样品模拟与实验的热导率,发现其在200~900 ℃的趋势相同,即都从200 ℃开始持续增加,在900 ℃达到峰值,可以说明此模拟是可行的。
(3)对于不同孔隙率下的(ZrxY(1-x/4)Ta(1-x/4)Ti(1-x/4)Er(1-x/4))O 陶瓷材料,孔隙与样品的元素组成对热导率的影响存在竞争关系,孔隙率偏小时元素组成对热导率的影响起主导作用,而孔隙率大于某一定值时,孔隙成为主要影响热导率的因素,即存在临界值。而在本研究中此临界值为6 .67%。
