主元法在导数问题中的应用
2023-04-15李振涛王淑玲
李振涛 王淑玲
(北京市顺义牛栏山第一中学)
主元法是指在利用两个或多个参数求解问题的过程中选择其中一个参数作为研究的主要对象,并将剩余的参数视为常量的思维方式.主元法在导数中的应用是把问题转换为关于主元素的公式,如方程或函数,这可以降低问题的复杂性,使其变得简单起来.
一、利用轮换式确定主元
含参问题是高考的必考题型,含有多个参数也是常见的题目,主元法是处理多元问题的一种重要方法.当参数的地位相等时,就可以看成是多项式中的轮换式,可以把其中的任意一个参数当做主元,另外的作为参数,这样可以降低问题处理的难度,是一种有效的方法.
【例1】(2022·北京卷·20节选)已知函数f(x)=exln(1+x).
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
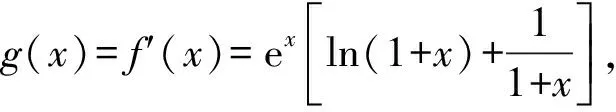
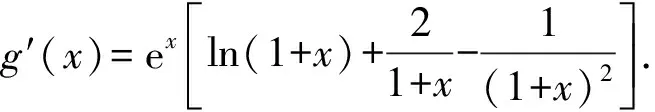
因为x≥0,所以ln(1+x)≥0,
所以g′(x)>0在[0,+∞)上恒成立,
所以g(x)在[0,+∞)上单调递增.
(Ⅲ)由于题目中s和t的地位相同,
所以以s为主元,t作为参数,
建立关于s的函数.
当然也可以t为主元,
s为参数建立关于t的函数.
证明:原不等式等价于f(s+t)-f(s)>f(t)-f(0),
令m(x)=f(x+t)-f(x)(x,t>0),
即证m(x)>m(0).
由m(x)=f(x+t)-f(x)=ex+tln(1+x+t)-exln(1+x),
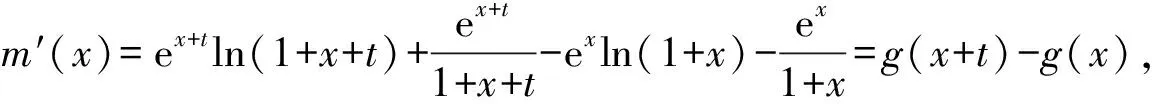
由(Ⅱ)知g(x)在[0,+∞)上单调递增,
所以g(x+t)>g(x),所以m′(x)>0,
所以m(x)在(0,+∞)上单调递增.
又x,t>0,所以m(x)>m(0),
所以对任意的s,t∈(0,+∞),
有f(s+t)>f(s)+f(t).
二、主元构造法
在导数问题中,由于大多数函数的图象不是轴对称图形,导致函数在某条直线两侧变化率不同,因此讨论这类问题时通常会出现两个变量,如何建立两个变量之间的关系,并统一成一个变量就是解决这类问题的关键,通过主元构造法就可以解决此类问题.

(Ⅰ)若f(x)≥0,求a的取值范围;
(Ⅱ)证明:若f(x)有两个零点x1,x2,则x1x2<1.
【解析】(Ⅰ)由题可知f(x)的定义域为(0,+∞),
令f′(x)=0,得x=1,
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,
则f(x)≥f(x)min=f(1)=e+1-a.
若f(x)≥0,则e+1-a≥0,即a≤e+1,
所以a的取值范围为(-∞,e+1].
(Ⅱ)证明:由(Ⅰ)知要使f(x)有两个零点,
则f(x)min=f(1)=e+1-a<0,即e+1 令t=x-lnx,x>0, 则f(t)=et+t-a有两个零点x1,x2等价于关于x的方程t=x-lnx有两个不相等的实根. 令h(x)=x-lnx, 易知h(x)在(0,1)上单调递减, 在(1,+∞)上单调递增. 不妨设0 又因为h(x)在(1,+∞)上单调递增, 所以F(x)在(0,1)上单调递增, 而F(1)=h(1)-h(1)=0, 即若f(x)有两个零点x1,x2,则x1x2<1. 【例3】(2019·全国Ⅲ卷理·20)已知函数f(x)=2x3-ax2+b. (Ⅰ)讨论f(x)的单调性; (Ⅱ)是否存在a,b,使得f(x)在区间[0,1]的最小值为-1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由. 【解析】(Ⅰ)由题意得f′(x)=6x2-2ax=2x(3x-a). ②当a=0时,f′(x)=6x2≥0对任何实数x恒成立, 所以f(x)在(-∞,+∞)上单调递增. 当a=0时,f(x)在(-∞,+∞)上单调递增; (Ⅱ)满足题设条件的a,b存在. (ⅰ)当a≤0时,由(Ⅰ)知, f(x)在[0,1]上单调递增, 所以f(x)在[0,1]上的最小值为f(0)=b, 最大值为f(1)=2-a+b, 当且仅当b=-1,2-a+b=1, 即a=0,b=-1时,满足题设条件. (ⅱ)当a≥3时,由(Ⅰ)知, f(x)在[0,1]上单调递减, 所以f(x)在[0,1]上的最大值为f(0)=b, 最小值为f(1)=2-a+b, 当且仅当b=1,2-a+b=-1, 即a=4,b=1时,满足题设条件. (ⅲ)当0 最大值为f(0)=b或f(1)=2-a+b. 与0 这与0 综上所述,当a=0,b=-1或a=4,b=1时, f(x)在[0,1]的最小值为-1,最大值为1. 在解决双变量问题时,利用主元法是一种比较好的方法,如果是对称轮换式,可以比较容易的以其中一个变量为主元,另一个变量为参数,建立一个函数关系,从而解决问题.如果函数是非轴对称问题,则利用非对称关系,将两元问题逐渐转换成一元问题,构造新函数从而解决问题;或者利用函数的单调性确定主元,再利用分类讨论解决问题.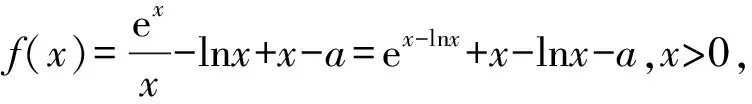

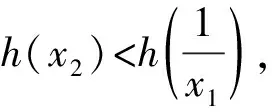
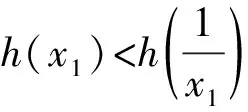
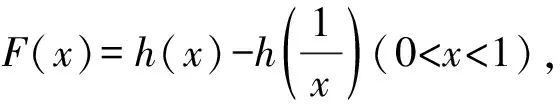
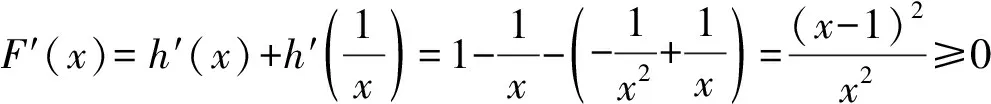
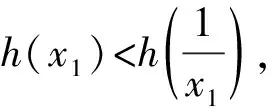
三、由单调性确定主元


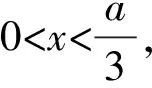
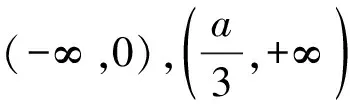

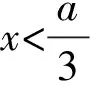
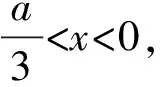
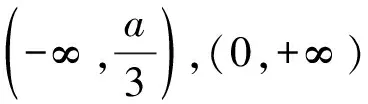
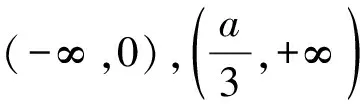
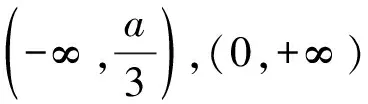
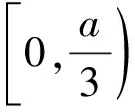
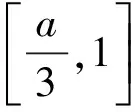
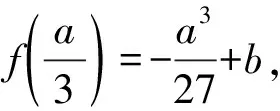


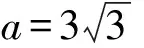
四、总结提升
