探索例题教学,深化思维过程

2023-04-14钟淑民

数学教学通讯·初中版 2023年3期

[摘要] 数学教学中教师常常采用例题教学让学生实现举一反三的能力，并渗透数学思想方法，以达到提升思维能力的目的. 例题教学不能停留于当前问题的解决，应该从一道题的解决推广到一类题的解决，使学生真正收获数学思维和思想.

[关键词] 例题教学;思维过程;举一反三

作者简介：钟淑民（1967—），本科学历，中学一级教师，从事初中数学教学与研究工作.

数学知识的学习中常常会用到“举例说明”的方法，即教师以例题进行教学引导学生学习一种解题方法或者某一知识点，因此这一教学方法的第一要务是提升学生运用新知解决问题的能力，加深学生对新知的理解，学习运用新知的技能，但是“举例说明”的方法如果止步于此，是远远不行的，这只是例题教学的初级阶段.

数学学习还要求学生能够“举一反三”，通过教师的例题教学“举一”，运用方法独立解决问题实现“反三”. 因此教师挑选例题时应该选择具有典型性和较大扩展空间的习题，才能更好地实现学生“举一反三”. 下面笔者通过教学实践谈一谈如何更好地进行例题教学，与各位同行交流.

优化例题教学过程，提升思维能力

在一次复习课中，笔者提出了一道非常典型的试题，现在将教学过程实录如下：

例1 直线a的一侧有两个定点A和B，如何在直线a上确定一点P，使得PA+PB最小？

（这个问题使学生纷纷陷入了思考）

生1：我想起来了，老师讲过这种题. 只要作直线a的垂线AM，垂足为M，再将AM延长到A′，使得AM与MA′相等，将A′B连接起来，那么线段A′B和直线a的交点就是我们要求的点P！（生1一边说一边演示，如图1所示）

这时其他学生慢慢想了起来，七嘴八舌地说：“哎呀，老师讲过，我怎么忘了呢！”

（此时笔者继续追问）

师：为什么这样做能使PA+PB最小呢？

生（异口同声）：因为两点之间线段最短.

师：为什么A′B的长最短，PA+PB就最小呢？

（学生开始窃窃私语，然后提到：根据证明可以得到PA与PA′相等，所以PA与PB的和等于A′B，如果A′B的长最短，那么PA+PB就最小）

师：那我们再思考一下，点P是唯一的吗？怎么才能证明直线a上的其他点不能满足这个条件呢？

（这时学生面露难色，他们没有想过这个问题）

本题虽然难度不高，但是设计精巧，内涵丰富，它具有在实际问题中构建数学模型的参考价值，同时含有对称变换思想方法的应用，还蕴含着几何中对“最值”问题的逻辑论证思路……这些内容是这道例题值得渲染的亮点，也是选择和讲解这道例题的内在价值.

因此，在本题的教学过程中，教师除了要让学生知道解法外，还要让学生体验数学思想方法的应用，从而提升思维能力，将这一解法在其他试题中进行推广，学会知识的迁移和运用，这才是解决这道例题的深层次的目的[1].

在教学过程中，教师还可以通过设置“问题串”的方式，引导学生参与问题解法的探究讨论，实现认识的升华.

优化教学过程：

师：这道题的目标是解决线段“最短”，那么在你学过的哪些几何知识中，见过“最短”的结论？又是怎样论述的呢？

生2：我们学过“两点之间线段最短”这个结论，还有一个结论是“直线外的点与这条直线上所有点之间的线段，垂线段最短”.

师：很好，这道题研究的也是“最短”，那么与你提到的这两个定理有什么区别？

生2：题目中的“最短”是两条线段的和，即一条折线段的最短，这是不一样的.

师：很好，这就是我们需要解决的问题. 我们知道，点A与点B之间最短的距离是线段AB的长，但是这与直线a上的点P是无关的，让我们无法找到解决问题的方法. 现在我们能否将问题分解一下，来推动问题解决呢？

生3：假设将点A移动到直线a的另外一边，那么线段AB与直线a就有了交点，这样是不是就有点P了……

师：很好！但是要怎样移动点A？要移动到直线a另外一边的哪里呢？

（学生开展集体讨论，纷纷发表自己的意见）

生4：作线段AA′与直线a垂直，垂足為M，并且使AM与MA′相等，通过证明△AMP与△A′MP全等，得到线段AP与A′P相等.

师：讲得太好了，这样就知道AP与PB的和等于A′P与PB的和，问题就转化成了A′P+PB何时是最小的.

生5：我们连接点B和点A′，与直线a的交点就是问题所求的点P！

师：这样我们似乎找到了正确的解法，但还有一个问题没有解决，点P是唯一的吗？怎样才能证明直线a上的其他点不能满足A′P+PB最小？

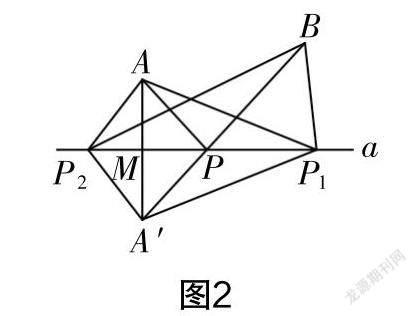
生6：如图2所示，假设直线a上有点P和点P，我们可以用一样的方法证明AP与A′P相等，AP与A′P相等. 通过三角形三条边的关系可以证明AP+BP，AP+BP都大于AP+PB.

师：看来我们只需要证明直线a上不是点P的任意一点相应的两条线段之和都大于AP与PB的和，就能够说明只有唯一的点P可以使AP+PB最小.

通过这样的方法，学生不仅学会并理解了本题的解法，而且通过亲身体验探究，以及参与寻找解题方法的探索过程，掌握了解题分析和思考的方法，初步认识了推理“最值”的逻辑方法，这些都为实现“举一反三”打下了坚实的基础[2].

强化例题解法理解，提升“举一反三”的能力

解决几何问题时经常需要添加辅助线，变换图形后再解决. 添加辅助线可使图形的位置移动，而图形的角、线段等大小不变或者按比例发生变化，它能促进问题得以解决，这样能使学生对辅助线的认识更加清晰，提高其解决几何问题的能力.

上述问题的解决过程中，学生认识到通过作线段AA′与直线a垂直（垂足为M），使得线段AM与MA′相等，这一辅助线构造了全等三角形，实际上是为了找到点A的对称点A′. 要探究“最小”的问题，当点A移动的同时，点P也会在直线上移动，需要保持AP与A′P相等. 因此，通过作辅助线进行图形变换，从更高层次的思维上来说是构造全等的或者成比例的线段.

教学中教师要提高学生作辅助线变换图形的能力，首先要培养学生对辅助线和图形的敏感度，增强学生认识和理解各类辅助线的意义，以及图形变换的意义和作用. 同时，教学中教师要通过例题讲解，引导学生以多种角度运用知识，进一步夯实对知识的理解，加深印象. 例如，笔者通过上述例题讲解示范后，列举习题进行检测，能考查学生对知识的掌握程度.

例2 桌球在桌面上滚动时，碰到台边会改变方向，向另一个方向沿着直线继续运动，由此可以知道它的变化规律：入射角与反射角相等. （如图3所示）

（1）如图4所示，桌球台内有一个位于点N处的白球和一个位于点M处的红球，请问将白球往桌球台边哪点撞击，可以通过反弹击中红球？

（2）如图5所示，桌球台内有一个位于点P处的红球和一个位于点Q处的白球，请问将白球向桌球台边哪点撞击，通过两次反弹可以击中红球？

列举例2的目的是让学生进一步理解和体验例1中的思想方法的运用，体验图形转换对解决问题的关键作用，使学生形成解决类似问题的重要思想策略.

例2与例1具有相同的性质和解决思路，学生能够仿照例1很快获得解决例2的路径，从而激发学习兴趣，增强学习数学的信心. 笔者发挥了教师应有的主导作用，组织学生探究和辨析解题方法，使学生能够根据入射角与反射角相等的原理，从第（1）问联想到轴对称变换，从第（2）问提升思维深度产生更加灵活的变化，学生在这一问中找到了解题方法，收获了成功的喜悦，激发了学习兴趣[3].

为了提升学生“举一反三”的能力，笔者加入了变式练习，让学生运用例1的解法去解决与例1的表象相距较远的问题.

例3 ∠AOB的边OB上有一个定点P，请在∠AOB的边OA上求一点Q和边OB上求一点R，使得PQ+QR最小.

（1）如图6所示，根据定理“直线外的定点与直线上所有点连接的线段中，垂线段最短”，可得点P到OA的最短距离是垂线段PQ的长，同理点Q到OB的最短距离是垂线段QR的长，此时PQ+QR最小. 以上说法正确吗？请说一说你的理由.

师：我们学过有关距离“最短”的定理，但是没有定理能够保证最小值的和一定也是最小值，因此上面的说法需要我们进行研究. 根据解答例1的经验，研究折线段的长最短的问题，需要我们将折线段向直线段靠拢，再进行比较. 因此，我们作以OA为轴的轴对称变换，得到射线OG′和点R的对称点R′，可知QR与QR′相等，这样PQ+QR等于PQ+QR′（如图6所示）. 同学们，仔细观察一下，你发现了什么？

生7：我发现，连接PR′，它与OA相交于点K，可以得到PK与KR的和等于PK与KR′的和（PR′），因为PR′小于PQ与QR′的和即PQ与QR的和，所以PQ+QR不是最小的.

师：你说得太精彩了，这样我们就证明了“最小值的和等于和的最小值”这个说法是不对的，同时也告诉我们数学猜想需要通过证明才能作为推理论证的依据.

（2）请你正确解答例3，并验证你的答案.

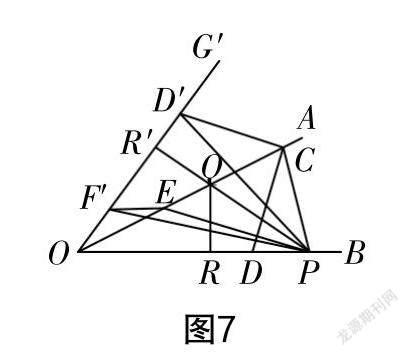
生8：在研究第（1）问的基础上，我们知道了经过对称变换后，原来的折线转化为了点P与射线OA、射线OG′上的点连起来的折线，如图8中的折线PEF′，PCD′，它们的长大于PF′，PD′的长，并且大于垂線段PR′的长. 设PR′与OA相交于点Q，点R与点R′关于OA对称，此时R使得PQ+QR最小，是我们要求的目标.

探究例3，是对例1的解法的深层次扩展，加深了学生对数学思想方法的认识，拓宽了学生的视野，奠定了学生在更加广阔的范围里使用这一思想方法的基础.

下面笔者继续安排例题发展这种解题能力，提高学生对移动图形的规划能力和变化方式的选择能力，以及学生灵活解题的能力.

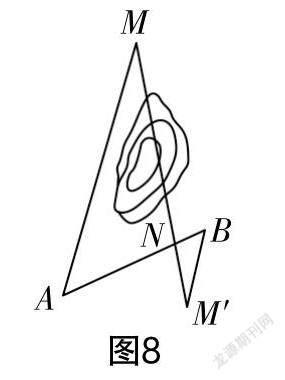
例4 如图8所示，从观测站A观测到北偏东方向有采油竖井M，距离为3.6千米，在采油竖井M的南面山丘后有一油罐车转运站N，它与观测站A的距离为1.2千米. 现要从转运站N处修一条输油管道到采油竖井M，但由于中间隔着山丘而无法直接测量距离和方向，请你设计一种方案，确定输油管道的长和方向.

例5 如图9所示，有一张三角形纸ABC，角C已经被撕掉了，怎样才能作出角C的平分线呢？请你想一想有哪些作法，并进行证明.

上述例4和例5属于同一类问题，解答目标较为隐蔽，通过图形变换使隐性的问题转变为显性的问题是解题的必然路径，教师除了要引导学生用轴对称方法外，还要帮助学生学会通过中心旋转和大小放缩等方法进行图形变换.

通过这些问题的分析和解决，学生能够实现从例1到例5的解题经验和知识的迁移，并根据具体的情况利用图形变换解决更多问题.

教学反思

例题教学的目标是通过一道题培养学生“举一反三”的能力，因此教学中教师要挖掘解题背后的思想方法和策略背景，让学生真正掌握一道题甚至一类题的本质，体会数学的精髓. 要提高例题教学的实效性，笔者认为需要关注以下几点：

（1）精选例题. 例题教学的关键是挑选典型和内涵丰富的习题作为例题，通过例题教学使学生掌握数学解题中经典的思想方法，对于知识的迁移具有较大的空间.

（2）精选系列例题. 例题教学并不是以解决一道题作为终点，而是要精心准备系列例题与典型例题相互呼应，巩固和拓展知识，为学生的知识运用打下基础.

（3）体验探究过程. 教师要积极组织学生探索例题解法，总结解题规律，体验数学思想和方法的应用，增强学生学习的信心，激发其学习兴趣.

（4）注重解题层次. 在例题研究时教师要层层递进、循序渐进，从与典型例题“形似”的例题开始拓展，到“神似”例题的研究，提高学生的解题能力，夯实知识基础.