高中物理的“举一反三”学习法
2016-11-24侯程迅
侯程迅
摘 要: 本文从一道高中物理学习中常见的习题入手,通过不断改变题设,利用整体法和隔离法对不同问法进行逐一解决,展现“举一反三”学习法的学习思路与优势,并对该学习法的习惯养成提出建议。
关键词: 高中物理 举一反三学习法 整体法 隔离法 习惯养成
美国著名教育家杜威曾说:“如果他不能筹划他自己解决问题的方法,自己寻找出路,他就学不到什么;即使他能背出一些正确答案,百分之百正确,他还是学不到什么。”现代教育已然不可能是古代“八股文”式的教育方式,虽然知识点不变,但是每年高考题目千变万化,出现原题几乎是不可能的。对于理科的学习尤其要杜绝“背诵式”学习,题海战术会在一定程度上提高学生的解题能力,但给学生带来的负担是巨大的,那么到底如何才能提高高中物理的水平呢?笔者的经验是采用“举一反三”的学习方法,那么题目虽多变,但万变不离其宗,很多题都是由母题变型而来,只要掌握了母题的解题方法,变型的问题不过是换汤不换药。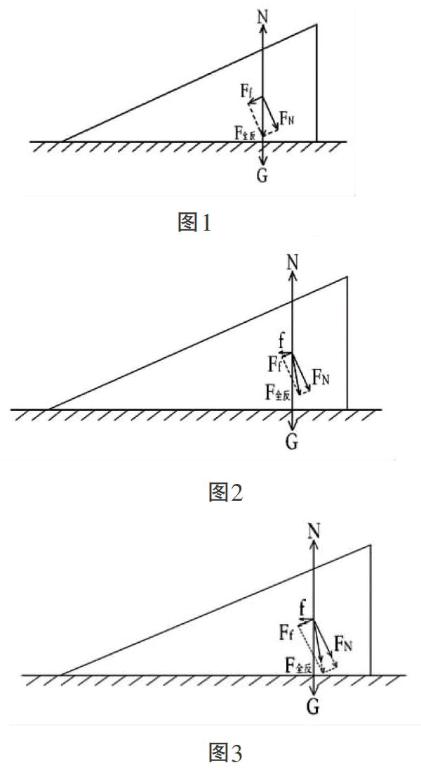
以一道常见习题为例:一物体恰能在一个固定斜面体上沿斜面匀速下滑,若沿斜面方向用力向下推此物体,使物体加速下滑,求斜面体受地面的摩擦力。
这是一道典型的连接体问题,对于连接体问题,我们最常用的就是整体法和隔离法,整体法常用于求整体所受外力,简单快捷,而求解所构成整体的两物体间的内力只能用隔离法。整体法和隔离法各有优势,在实际力学问题解答中,常常将两种方法结合起来使用。
此题比较简练,难度也偏低,但笔者做完此题后思考,此题的解答是以物体开始时匀速下滑为基础的。如果改变题设,物体开始时以某一加速度a匀加速下滑,施加推力F前后,斜面体受地面摩擦力的大小和方向将怎样变化呢(引申一)?
前两种问法中,物体所受推力F沿斜面方向这个条件给解题带来了便利,但笔者想如果在第二种问法的基础上将力F改为其他方向,如垂直于斜面方向,但保证物体与斜面仍存在相互挤压,在施加力F后,斜面体受地面摩擦力的大小和方向又将会怎样变化(引申二)?
思考到这里,我们不妨更大胆地猜想,如果我们进一步将上面的问题推至一个更普遍的情况,在确保物体与斜面体存在相互挤压的前提下,直接将特定方向的推力换成任意方向的推力,那么施加推力前后,斜面体受地面摩擦力的大小和方向会怎样变化(引申三)?
经过几次引申,一道在特殊条件下求解的简单题型,已经被推广到具有较高普遍性的结论,不局限于一道题目,不断挖掘题目背后的物理内涵,知道每个条件想表达的是什么,并不断引申,这就是笔者想和大家分享的学习方法——“举一反三”学习法。
很多同学习题书做了一本又一本,不仅给自己带来了很重的学业负担,成绩还没有得到明显的提升,导致效率低下。现在学校的老师也告诉我们“多做题”不如“精做题”的思想,要学会“举一反三”,但具体如何实现通常需要更多探索学习。那么如何掌握“举一反三”的学习方法呢?笔者认为主要是注意养成良好的学习习惯,做到以下几点:首先,培养独立思考问题的能力;不要一有点问题就看答案或询问他人,即使做对题目,也不要急着做完就过,试着从多角度思考问题,能由此及彼。其次,选择进行适当的练习。题目的训练在“精”不在“多”,必要的练习有助于提高解题能力;完整细致地做完一套经典的教辅资料比“刷题”更有意义。选题时,常常不仅要考虑习题的代表性、难易度、系统性,更要结合考虑本人的学习状况与计划。此外,对自己练习的结果进行自我评价,不断总结与拓展;对于同种类型的问题,要学会做笔记,自己总结相似题型的联系,题目都是出题老师的视角,体现出对所学知识的理解与运用能力的检测,多站在宏观的视角看问题,有助于把握出题规律,强化思维与运用能力。
学生应该学习的不仅仅是怎么解题,更应该注重学习方法,提高效率与能力。中国古代伟大教育家孔子十分注重培养举一反三、触类旁通的逻辑推理能力;能根据已有知识,整理总结并扩展运用,逐渐构建知识体系,提高创新运用能力是学习的主要目的。现代教育中“死记硬背”式的学习越来越跟不上时代的潮流。培养独立思考和深化思维的习惯与能力,在学习中能由“一”想到“三”,无疑是提高学生综合运用能力的必要途径,必然有益于提高我们的创新能力,作为新时代的接班人,创新能力是决定我国核心竞争力的重要因素。
参考文献:
[1]赵辉.高中“整体法”和“隔离法”的渗透[J].物理通报,2012(01).
[2]张新凤.谈高中力学解题思路与基本技巧[J].数理化学习,2012(07).
[3]刘鹏.浅谈高中力学的解题思路及技巧[J].亚太教育,2015(25).
