一道导数联考题的命制创新与解法分析*

湖北省恩施州教育科学研究院 (445000) 周 威

湖南省长沙市雷锋学校 (410217) 童继稀

一、命题灵感与创新

2022届湖北省七市(州)3月联考，备受学校和社会关注，命题质量要求较高，而其经典压轴的导数综合题，自然成为关注焦点.结合近几年的高考考查趋势，此次联考导数综合题的多维双向细目表设置如下：

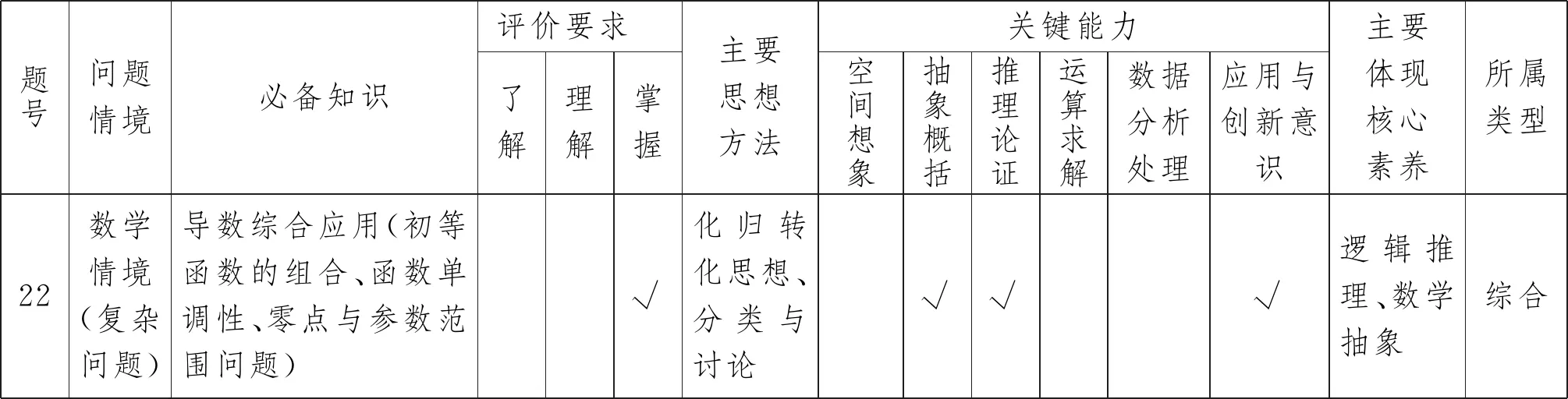
表1 导数综合题双向细目表

那么，如何根据表中必备知识、关键能力要求命好这道导数综合题呢？这肯定少不了高考导向与灵感创新．

1．高考导向下的命题灵感

首先，根据必备知识要求，从2021年新高考Ⅰ卷导数题中寻找灵感．

例1 (2021年新高考Ⅰ卷22题)已知函数f(x)=x(1-lnx)．

(1)讨论f(x)的单调性；

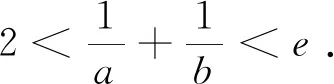
其次，注意到2021年新高考Ⅱ卷导数题综合考查了含双参数的关于零点个数问题，试题呈现如下：

例2 (2021年新高考Ⅱ卷22题)已知函数f(x)=(x-1)ex-ax2+b．

(1)讨论f(x)的单调性；

思考到这里，双向细目表中的“初等函数的组合、零点与参数范围问题”要求，就有了命题灵感，那就是y=xlnx与二次函数的组合成一个新函数g(x)=xlnx-ax2+b+cx．

接下来的问题是考查一个参数还是两个参数问题，以及如何确定参数a,b,c的值？考虑到文[2]中对含双参数函数的零点分类讨论的复杂性，还是选择单参数.另外，注意到对g(x)求导后有g′(x)=lnx+1-2ax+c，设置c=-1方便进一步计算．同时，设置b=1，此时g(1)=-a恰好只含有参数部分．因此，新函数确定为g(x)=xlnx-ax2-x+1，从而设置试题命制初稿如下：

例3 已知函数g(x)=xlnx-ax2-x+1．

(1)当a=0时，讨论函数g(x)的单调性；

(2)试讨论函数g(x)的零点个数．

2．基于“解决问题能力”的命题创新

在对例3第(2)问的计算过程中发现，

若

若

如图1所示，g(x)在(0,m)上单调递减，在(m,n)上单调递增，在(n,+∞)上单调递减．

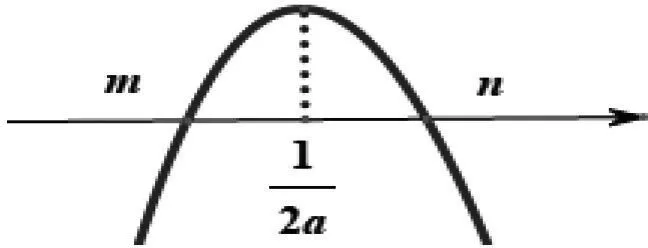
图1

由g(m)=mlnm-am2-m+1=am2-m+1<0，可知g(n)=nlnn-an2-n+1有三种情况，如图2所示，且g(n)=0时n为“隐零点”，n的值求不出来，这为后面的讨论带来了困难，因此这就需要对题目进行再修改.

g(n)=0

(1)证明：函数f(x)在(1，+∞)上有且仅有一个零点；

(2)假设常数λ>1，且满足f(λ)=0，试讨论函数g(x)的零点个数．

二、试题解法分析

例4第(1)问的证明较为简单，分值设置为3分，具体证明过程如下：

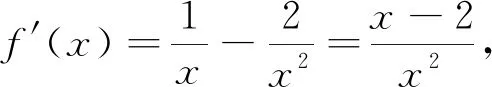
结合单调性得f(x)在(1，+∞)有且仅有一个零点．

例4第(2)问可以从分类讨论角度进行求解，也可以从半分离参数或分离参数的角度进行求解，思路入口宽，即实现了导数综合题两种常用方法的考查，考查了学生在具体实践中的问题解决能力.

解法1：(分类讨论)由题意

当a=0时，g(x)=xlnx-x+1，g′(x)=lnx．令g′(x)=0，解得x=1，则g(x)在(0,1)上单调递减，在(1,+∞)上单调递增，g(x)min=g(1)=0，可得g(x)只有一个零点．

当a=0时，y=ax图像与φ(x)图像有一个交点；

当a<0时，y=ax图像经过二、四象限，与φ(x)图像无交点；

结合(1)可知，φ(x)在(0,1)上单调递减，0在(1,λ)上单调递增，在(λ,+∞)上单调递减，如图3所示．又

图3

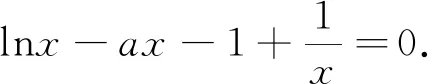
令函数φ(x)=ax2-x+1,x∈(0,+∞)．

同(1)问，可证函数f(x)在x∈(0,1)单调递减，则h(x)min=f(x0)>f(1)=0，可得函数h(x)在(0,+∞)无零点．

当a=0时，可得x∈(0,1)时，φ(x)>0，即h′(x)<0，则函数h(x)单调递减；x∈(1,+∞)时，φ(x)<0，即h′(x)>0，则函数h(x)单调递增，有h(x)min=h(1)=0，故h(x)在(0,+∞)只有一个零点．

当a>0时，根据判别式Δ=1-4a的符号分情况讨论．

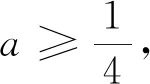
可得函数h(x)在(0,+∞)只有一个零点．

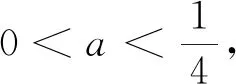
则函数h(x)在(0,1)有一个零点；而在(1,+∞)的零点个数由极大值h(x2)的符号决定，函数h(x)图象有图4的3种情况如下：

图4

三、考试结果评价与结语

结合上述命题意图和考试结果分析，在二轮复习教学中，依然要注重基础知识和基本解题技能的渗透，对优秀学生的计算能力、转化化归能力、直观想象能力进行专项突破，对函数导数板块知识做好分层教学，因材施教，使得不同思维水平的学生的得分均得到体现．