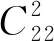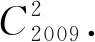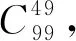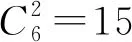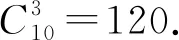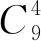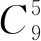一类不定方程整数解问题的求解策略
2023-04-03江苏省徐州市第一中学221004
江苏省徐州市第一中学 (221004) 许 丽
1.基本问题的求解模型
问题n元一次不定方程x1+x2+…+xn=m(m≥n≥2)的正整数解(x1,x2,…,xn)的组数是多少?
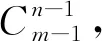
竞赛对这一类不定方程问题情有独钟,常考常新.梳理近些年各省的预赛和全国联赛中有关n元一次不定方程的考题,发现这类问题在方程形式和解的制约关系等方面不断进行变化,通过改变方程的形式、增加限制条件、包装成别样面目等,将这类问题演绎得绚丽多姿,精彩纷呈.
2.形态多样的不定方程
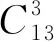
例2 (2009湖北预赛)求不定方程x1+x2+x3+3x4+3x5+5x6=21的正整数解的组数.
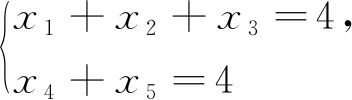
例3 (2021福建预赛)设整数a,b,c满足0≤a≤10,0≤b≤10,0≤c≤10,10≤a+b+c≤20,则满足条件的有序数组(a,b,c)共有组.
解析:令a+1=x,b+1=y,c+1=z,则1≤x,y,z≤11,13≤x+y+z≤23.
例4 (2018上海预赛)求不定方程x+y+z+w=25满足x 例5 (2010全国高中数学联赛)方程x+y+z=2010满足x≤y≤z的正整数解(x,y,z)的个数是. 3.千姿百态的广泛应用 例6 (2002全国高中数学联赛)已知两个实数集合A={a1,a2,…,a100}与B={b1,b2,…,b50},若从A到B的映射f使得B中每个元素都有原象,且f(a1)≤f(a2)≤…≤f(a100),则这样的映射共有( ). 例7 (2012黑龙江预赛)将10个相同的小球装入编号为1,2,3的三个盒子(每次要把十个球装完)中,要求每个盒子里球的个数不少于盒子的编号数,则这样的装法种数为. 例8(2013辽宁预赛)将11个完全一样的小球放入6个不相同的盒子中,使得至多有3个空盒子的方法种数为. 例9 (2011内蒙古预赛)各位数字之和等于11的四位数的个数为. 例10 (2020浙江预赛)已知由6个正整数组成的六位十进制数中,其个位上的数字是4的倍数,十位和百位上的数字都是3的倍数,且六位数的数码和为21,则满足上述条件的六位数的个数为. 解析:由题意知,该六位数后三位(百位、十位、个位)上的数字所有可能为:334,364,394,634,664,934,338,368,638. 例11 (2021上海预赛)在正整数1,2,…,20210418中,有多少个数的数码和为8? 解析:设这样的正整数为n. 例12 (2016河北预赛)如果从数1,2,3,…,14中按由小到大的顺序取出a1,a2,a3,使得同时满足a2-a1≥3,a3-a2≥3,那么符合要求的不同取法数为. 例13 (2018湖北预赛)一枚骰子连续投掷4次,从第二次起每次出现的点数都不小于前一次出现的点数的概率为. 例14 (2022重庆预赛)将一枚骰子连续投掷五次,则事件“五次出现的点数既不全相同,也不两两互异,且从第二次起每一次的点数都不小于前一次的点数”的概率为.