基于自适应TQWT与小波包奇异谱熵的滚动轴承早期故障诊断

2023-03-29谢锋云刘慧胡旺姜永奇

铁道科学与工程学报 2023年2期

谢锋云，刘慧，胡旺，姜永奇

(华东交通大学机电与车辆工程学院，江西南昌 330013)

滚动轴承是机械传动设备的重要组成部分，广泛应用于各类交通运输设备、工业生产设备，其健康状况与设备正常工作有着密不可分的关系，若在滚动轴承早期故障阶段就敏感地检测到其故障的发生，可以达到减少经济损失以及保护人身安全的效果。在机械设备生产工作过程中，由于变转速和变工况的影响，传感器采集到的信号大多表现为非线性和非平稳性。短时傅里叶变换(STFT)、经验模态分解(EMD)和小波分析等是常用的非线性、非平稳信号处理方法。STFT 的窗函数一经选定，在变换过程中便不能进行更改，不能反映频率随时间的变化[1]；EMD的理论基础不够完善，且在信号分解过程中存在端点效应和模态混叠等问题[2]；小波分析具有优良的时频分析能力，受到了业内人士的热爱[3]。但运用小波分析对信号进行处理的效果依赖小波基的选择，且在处理过程中小波基一旦选定便不能更改，选择不当对信号的处理效果会有很大的影响。基于此，SELESNICK[4]提出一种新的品质因子可调的时频分析方法，即可调品质因子小波变换(TQWT)，它能够通过调节参数品质因子Q和冗余因子r，为信号匹配符合其振荡特性的小波基函数，达到更好的分解效果。龙莹等[5]采用改进谱峭度(Improved spectral kurtosis, ISK)的TQWT，对齿轮箱轴承故障进行了有效诊断。ZHANG 等[6]采用TQWT 对信号进行处理，并利用频域定义的1.5D 谱峭度分离出有用的故障特征频带和干扰频带。KONG 等[7]提出一种新的基于自适应TQWT 滤波器的特征提取方法来检测重复瞬态，将该方法应用于故障轴承振动信号，验证了其有效性。小波包奇异谱熵是将小波包分解与奇异谱熵相结合的一种故障特征提取方法。小波包分解不仅可以对信号的全频率成分进行较为完整的分解[8]，还可根据信号特性和分析要求自适应选择相匹配的频带与频谱，从而从信号中更有效地提取信息[9]。奇异谱熵能够反映信号的复杂性与时序性。周建民等[10]通过将小波包奇异谱熵和支持向量数据描述(SVDD)相结合对滚动轴承性能退化进行了评估。针对滚动轴承早期故障的特点，本文提出一种将TQWT 与小波包奇异谱熵相结合提取故障特征，SVM 模式识别的滚动轴承故障诊断方法。利用网格搜索法对TQWT的最佳品质因子进行搜索，并以峭谱积最大化为评价标准确定最佳品质因子，利用中心频率比确定合适的分解层数，将得到的参数对信号进行TQWT 分解并单支重构，将峭谱积最大的重构分量的小波包奇异谱熵值作为故障特征向量，运用SVM 进行故障状态的判断，并与未进行TQWT 处理、以峭度和包络谱峰值因子单独作为TQWT 优化指标的信号的SVM 识别结果比较，对比结果显示，本文所提方法处理后的信号的识别率得到了一定程度的提升。

1 基本原理

1.1 TQWT

TQWT 是一种从频域滤波角度设计而成的离散小波变换方法，与传统小波变换品质因子(信号的中心频率fc 和带宽BW 的比值)恒定相比，它根据待分析信号的振荡特性来选择品质因子，通过迭代双通道滤波器组和离散傅里叶变换(DFT)以迭代的方式实现信号的分解、重构[11]。

TQWT 由一个个小波基函数组成，每个基函数由3 个可调的参数(品质因子Q，冗余度r和分解层数J)控制，参数不同，输出的小波基函数的形状和性质也不同。其中，Q和r与低通尺度因子α以及高通尺度因子β的关系满足：

TQWT 的Q和r确定了，可以通过式(2)确定TQWT理论允许的最大分解层数Jmax。

其中：[·]为向0取整；N为待分析信号的长度。

品质因子Q定义为滤波器中心频率与带宽的比值。它用来描述信号的振荡属性(小波振荡持续的时间)，可以反映信号的振荡程度，Q越大，振荡越强烈。品质因子Q的选择决定着最终滤波频带的选择，合适的频带评价指标是保证最终滤波效果的关键。本文使用能够表征信号冲击性和周期性的时频域指标——包络谱峰值因子(Crest factor of envelope spectrum, Ec)[12]与信号的峭度值的乘积——峭谱积，对最佳的Q进行挑选。根据文献[11, 13]，本文Q的遍历范围选择为[1,5]。

r是计算无穷多级时TQWT 的冗余度，通常r≥3。冗余因子决定了小波频响间的重合度，r越大，则频响重合度越高。根据文献[14-15]，本文设定r=3。

分解层数J表示双通道滤波器组的数目。分解层数过大不仅会降低运算速度还会导致冗余信号分量过多，这些分量由于带宽太窄而无法囊括足够的特征信息，对于故障特征提取来说意义不大，并且会造成计算资源的浪费。本文使用中心频率比来确定合适的分解层数[13]。

1.2 峭谱积

包络谱峰值因子考虑了共振频段能量较大且滤波信号周期性较强的特点。定义为：

式中：Amax为包络谱在[n*fr，fs/2]范围内的最大幅值；Arms为均方根值。Ec值越大，信号包含的周期性和冲击性越强，反之亦然。

峭度是表征信号的冲击性强弱的时域指标，其计算公式为：

其中：μ为信号的均值；σ为信号的标准差。

峭谱积的表达式为：

它在包络谱峰值因子的基础上，加强了对信号冲击性的度量，KEc越大，信号的周期性和冲击性越明显，反之亦然。

1.3 中心频率比

中心频率比的定义为：

合理分解层数停止准则表示为：

其中：T为合理的中心频率比阈值，推荐选择值为0.02～0.05[13]，本文设置阈值T=0.05。因此，合理的分解层数Ja选择为：

1.4 小波包奇异谱熵

1.4.1 小波包奇异谱熵原理

小波包奇异谱熵是将小波包分解、奇异值分解与信息熵融为一体的特征提取方法。求取信号的小波包奇异谱熵的步骤为：对信号进行小波包分解，对分解后的系数进行重构，并将重构后的系数矩阵进行奇异值分解，求归一化后的奇异值的信息熵，从而对信号的复杂程度给出一个确定的量度[10]。

1.4.2 小波包分解层数及小波基的选择

由文献[16]可知，如果只是检测信号奇变的突变点，按照规则性系数相似方法，选择规则性系数较小的小波基波会得到较好的结果，所以本文选择db10小波基进行小波包分解。

王婉秋等[17]指出，对于滚动轴承振动信号，小波包的分解层数应该满足：

式中：J为最大分解层数；fs为采样频率；f为信号的故障频率。经过计算，本文所用信号的小波包分解的最大分解层数为6层，本文小波包分解层数选择3层。

2 故障诊断流程

为提取滚动轴承早期故障的微弱故障特征，对滚动轴承的早期故障状态进行有效识别，本文提出一种自适应可调品质因子与小波包奇异谱熵相结合提取故障特征的方法，运用支持向量机对提取的故障特征进行模式识别，诊断流程如图1所示。

图1 故障诊断流程图Fig. 1 Fault diagnosis flow chart

具体的步骤为：

1) 确定TQWT最佳的品质因子Q。

依据文献[11, 13]，设定Q的寻优范围为[1, 5]，遍历步长为0.1。分别对41种情况下的[Q,r]组合进行TQWT 分解，并单支重构，计算单支重构后各重构分量的峭谱积KEc，最大的KEc对应的Q值即为最佳的Q值。

2) 利用中心频率比确定TQWT 合适的分解层数J。

3) 利用得到的Q和J对待分析的信号进行TQWT 分解，并单支重构，计算各重构分量的KEc，挑选出每组信号KEc最大对应的重构分量为新的待分析的信号。

4) 对得到的新的待分析信号提取小波包奇异谱熵值，作为故障特征向量。

5) 运用支持向量机对得到的故障特征向量进行模式识别。

3 实验平台与实验分析

运用XJTU-SY 滚动轴承加速寿命试验数据集验证本文所提方法的有效性，试验所用的轴承平台如图2 所示[18-19]。该平台由数字式力显示器、电机速度控制器、支撑轴承、测试轴承、交流电机、液压加载系统以及加速度传感器等设备搭建而成，可用来测试在不同工况下的轴承的加速度振动信号。实验验证所用数据的具体信息见表1。选取外圈、内圈和保持架故障产生初期的信号作为早期故障信号，加上轴承正常运行时的数据，共4种运行状态，运用本文所提方法进行分析验证。

表1 实验相关参数信息Table 1 Experimental related parameter information

图2 试验平台Fig. 2 Test platform

由采样频率和转速等信息可计算出轴承转一圈大概会产生683个采样点，为保证每组样本包含足够的故障信息，设置每组样本长度为2 048 个采样点，每种状态200 组样本，共800 组样本。任选保持架故障的一组样本进行验证展示，图3为该组保持架故障原始信号的时域波形图。

图3 原始信号时域图Fig. 3 Time domain diagram of original signal

对41 种[Q,r]组合进行TQWT 分解与单支重构，计算重构后分量的KEc值，图4 为41 种[Q,r]组合下得到的该组样本的KEc最大值的曲线图。从图中可以得到，最大KEc值对应的Q值为Q=1+利用得到的Q值，结合式(2)计算出该组样本TQWT 分解时的最大分解层数为35，利用中心频率比计算合适的分解层数为24。

图4 不同[Q,r]组合下的最大KEc值曲线Fig. 4 Maximum KEc curves under different [Q,r] combinations

对待处理信号运用得到的[Q,r,J]值进行TQWT分解并单支重构，计算重构后各分量的KEc值，挑选最大的KEc值对应的重构分量为新的待处理的信号。图5为TQWT处理后的信号的时域波形图。可以看到TQWT 处理后信号的幅值有所下降，但信号的周期性得到了增强。

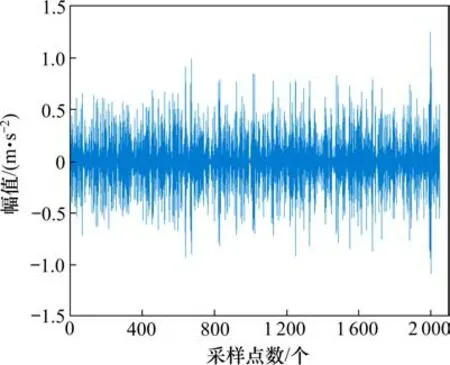
图5 TQWT处理后信号时域图Fig. 5 Time domain diagram of TQWT processed signal

对TQWT 处理后的信号提取小波包奇异谱熵作为故障特征向量。图6 为4 种状态TQWT 处理后一组信号的小波包奇异谱熵值对比，图7 为4 种状态原始信号的小波包奇异谱熵值对比。从2幅图的对比可以看出，TQWT 处理后4种状态的小波包奇异谱熵值的区分度更高。

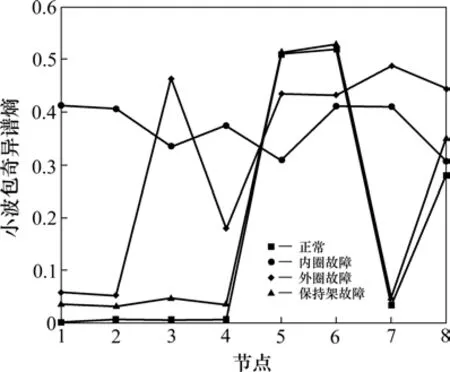
图6 TQWT处理后4种状态的小波包奇异谱熵值对比Fig. 6 Comparison of singular spectral entropy values of wavelet packets in four states after TQWT processing

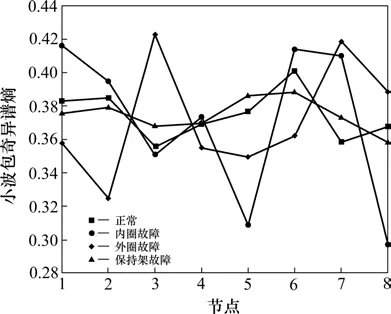
图7 4种状态原始信号的小波包奇异谱熵值对比Fig. 7 Comparison of the singular spectral entropy values of wavelet packets of four original signals

对得到的故障特征向量运用SVM 进行故障状态的识别，其中50组用于模型的训练，150组用于测试。图8 为TQWT 处理后的信号的SVM 识别结果。图9 为原始信号的SVM 识别结果，图10 和图11 分别为TQWT 优化指标为峭度和包络谱峰值因子的识别结果。

图8 TQWT处理后信号SVM识别结果Fig. 8 SVM recognition result of TQWT processed signal

图9 原始信号识别结果Fig. 9 Original signal recognition result

图10 TQWT优化指标为峭度识别结果Fig. 10 TQWT optimization index is kurtosis recognition result

图11 TQWT优化指标为Ec识别结果Fig. 11 TQWT optimization index is Ec identification result

为使上述识别结果更加直观，引入了混沌矩阵，详细分析了本文所提方法、未进行TQWT 处理、TQWT 优化指标为峭度和包络谱峰值因子的识别结果，如图12所示。

图12 4种模型识别结果混沌矩阵Fig. 12 Confusion matrix of identification results of four models

从以上SVM 的处理结果对比发现，利用本文所提峭谱积为优化指标对信号TQWT 处理后，识别率较未进行TQWT 处理的提高了约7%，与TQWT 的优化指标为峭度和Ec 的识别结果相比识别率也有提高，但以峭度和Ec 为优化指标时，虽然识别率与未进行TQWT 处理时相比有了提高，但出现了将内圈和外圈故障识别为正常状态的样本，这在故障诊断领域是不被允许的。