高速铁路钢轨上拱不平顺对波磨萌生的影响研究
2023-03-29张向民张勇
张向民,张勇
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 广东梅龙铁路有限公司,广东 广州 510101)
高温天气下高速铁路无砟轨道长钢轨产生上拱变形。如津滨城际无砟轨道有3处钢轨上拱,上拱量达12 mm;武广高铁胡家湾大桥在轨温约50 ℃时发生6 mm 的钢轨上拱[1],该处发生了钢轨波磨病害,并出现弹条断裂伤损[2]。赣龙铁路枫树排隧道也出现了钢轨上拱导致扣件弹条断裂现象[3]。长钢轨长波长单波上拱属于轨道垂向不平顺类型之一,其产生原因主要是由钢轨内累积温度力引起的。胡家湾大桥钢轨上拱和钢轨波磨相伴相生,它们之间是否有什么内在联系?钢轨波磨问题是世界铁路行业尚未解决的重大技术难题,研究其萌生机理并找出解决问题的办法,具有重要技术经济和理论意义。关于钢轨波磨萌生的机理有各种各样的推测,但归结起来可分为动力论和非动力论,动力论认为波磨是由轨面不平顺激励的振动引起的,而轮轨接触力波动是最重要的影响因素[4-8]。随着我国高速铁路的不断发展,波磨伤损问题也逐渐凸显,许多学者针对这一问题开展了研究[9-13]。司道林等[9]在高速铁路波磨调研和现场测试中发现轮轨系统垂向共振是导致钢轨波磨的主因;肖乾等[13]提出轮轨摩擦自激振动、轨道-车辆系统零部件结构共振等因素是导致轮轨激励形成的根本原因。受胡家湾大桥钢轨上拱与波磨相伴相生的启发,有必要将无缝线路理论引入到波磨萌生机理研究中。钢轨上拱不平顺激励轮轨系统共振,产生大幅值轮载,引起轮轨接触力超过钢轨钢安定极限,导致钢轨波磨萌生,钢轨上拱、轮载和轮轨接触力之间关联过程简述如图1所示。本文试图通过建立涵盖温度力引起钢轨上拱、大幅值轮载和轮轨接触力计算理论的统一数力学模型,研究钢轨上拱矢度、列车参数、轨道参数的影响规律,详细阐述“钢轨上拱-轮载-轮轨接触力相互作用”对于钢轨波磨萌生机理、减磨措施以及车轮多边形发生机理的启示意义,展望此类型钢轨波磨研究中的前沿问题,为该领域今后研究提供方向和借鉴。

图1 钢轨上拱、轮载和轮轨接触力之间的关联过程简述Fig. 1 Brief description of the correlation process between rail uplift-wheel load -wheel-rail contact force
1 钢轨上拱模型建立
基于能量法,建立无砟轨道长钢轨垂向上拱分析模型,综合考虑作用于系统的钢轨弯曲部分及两端邻区变形功、钢轨弹性弯曲变形能、扣件垂向变形能以及钢轨重力势能,构建长钢轨上拱总能量方程,运用势能驻值原理推导长钢轨垂向变形温度力解析解,分析随着长钢轨上拱变形全过程各部分能量的占比变化规律,研究扣件参数对钢轨上拱的影响规律。
1.1 钢轨垂向上拱公式推导
无砟轨道长钢轨垂向上拱变形曲线为单波,其波形函数应同时满足力学和几何边界条件,即y=0,y'=0,y″=0,波形函数表达式见式(1)[14]。
长钢轨垂向上拱系统总能量A由5 部分组成,各部分能量的推导过程可参考文献[14]。
1) 长钢轨弯曲部分两端邻区变形功A1:
2) 长钢轨弯曲部分伸长变形功A2:
由弯曲弧长伸长量变化得出上拱矢度f,波长l和θ之间的关系式:2.756其中:t=f0l
3) 长钢轨弹性弯曲变形能A3:
4) 扣件垂向变形能A4:
5) 钢轨重力势能A5:
依据势能驻值原理,由∂A/∂f=0 和∂A/∂l=0 可分别得出钢轨温度力Pt的解析式:
1.2 系统各组成能量占比分析
由式(4),式(8)和式(9)可建立关于变量Pt,f,l和θ的非线性方程组,相关计算参数取值见表1,其中γ1,γ2和γ3由数值积分获得,扣件垂向刚度采用式Q=Cyh计算[1],由文献[15]扣件垂向刚度试验数据经多项式回归得出Q=1 852.9y1.1(y≤4 mm)。随着上拱矢度的增加各部分能量占比变化关系如图2和表2所示。

表1 垂向上拱相关计算参数取值Table 1 Calculation parameters values of uplift

图2 各部分能量占比分析Fig. 2 Analysis of the energy proportion of each part
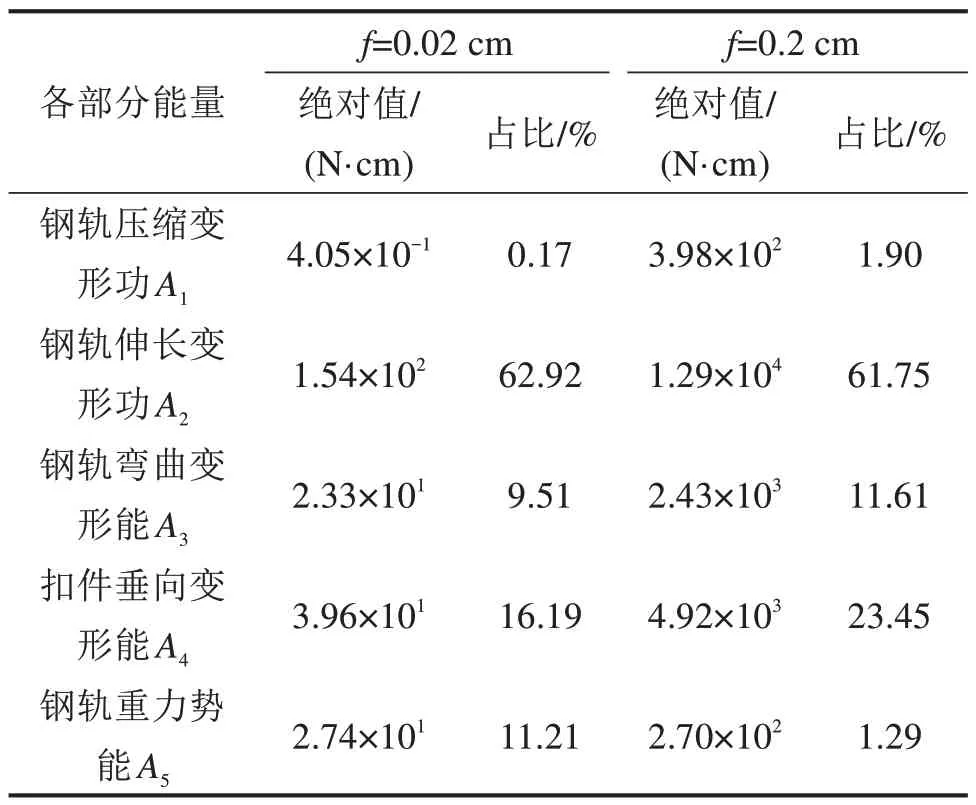
表2 各部分能量变化及占比Table 2 Energy change and proportion of each part
计算结果表明,在上拱的初始阶段(如f=0.02 cm),钢轨伸长变形功A2,扣件垂向变形能A4及钢轨重力势能A5之和占比超过90%,而在上拱的发展阶段(如f=0.2 cm),A2和A4及钢轨弯曲变形能A3之和占比超过90%,其中A2和A4始终是占比最大的能量,两者之和超过80%。A2由钢轨自身材料力学性质和截面参数表征,我国高速铁路统一采用60 kg/m 钢轨,其数值基本相同,而A4由扣件垂向刚度和扣件间距控制,扣件系统性能具有随机性。因此,扣件系统参数应为抑制钢轨上拱的关键参数。扣件垂向刚度如果衰减50%,温升幅度由正常值71.7 ℃降至50.8 ℃,降低29.1%;小阻力扣件温升幅度为48.3 ℃,相较于常阻力降低了32.6%。如果小阻力扣件刚度衰减50%,温升幅度将降至38.0 ℃,降低21.3%,可知小阻力扣件刚度衰减后抵抗钢轨垂向变形能力急剧下降,极易形成钢轨上拱病害。
2 钢轨上拱引起大幅值轮载模型建立
当列车通过钢轨上拱变形地段时,钢轨会受到车轮的冲击作用,产生大幅值轮载,选取钢轨上拱最高点分析轮轨冲击力,建立轮轨冲击模型,如图3 所示,大幅值轮载公式的推导可参考文献[16-17],并对文献中轮载公式的错误进行了修正,计算表达式见式(10)。大幅值轮载Wd与无砟轨道整体垂向刚度kr,阻尼Cr,列车静轮载Ws以及簧下质量m0相关,车轮跌落高度h等于钢轨上拱矢度f。该模型曾用于分析日本951型试验列车超大轮载产生机理[17],并得到日本东海道新干线现场试验验证。
轨道垂向刚度kr和阻尼Cr可由落轴试验获得,采用CRH2型动车和弹性支撑块式无砟轨道相关参数,由式(10)计算钢轨上拱矢度对列车动轮载的影响见图4,钢轨上拱0.5 mm 可使动轮载增加2.3倍。

图4 钢轨上拱与列车轮载关系Fig. 4 Relationship between uplift and wheel load
3 轮轨接触力计算及参数影响分析
钢轨上拱导致列车产生大幅值动轮载,并使轮轨接触力增大。采用Hertz 理论求解轮轨接触法向应力;依据单一圆弧型踏面轮轨接触模型[18]获得轮轨接触几何参数,得到蠕滑率ξi,通过Kalker线性理论求解轮轨接触切向力并依据沈氏理论[19]进行修正;将轮轨接触法向应力与钢轨钢的安定极限进行对比分析,据此判断钢轨顶面的安定状态。
3.1 轮轨接触力计算方法
1) 轮轨接触法向应力计算。基于Hertz 理论[8],计算表达式见式(11)。
没有上拱的钢轨曲率半径为R21=+∞,钢轨上拱后曲率半径取为其中y为钢轨上拱曲线函数。钢轨上拱时,轮轨接触动载荷P由式(10)获得。
2) 轮轨接触切向力计算。轮轨滚动接触几何参数由单一圆弧型踏面接触模型获得,蠕滑率见式(12)。因轮对横移量yG与轮对摇头角φ数值较小,则横移速度与滚动速度之比ẏG/v0和r0φ̇/v0可参考磨耗型踏面相关轮轨蠕滑率取值[8]。
轮轨接触可视为准统一Hertz 稳态滚动接触问题,由Kalker 线性蠕滑理论[20]得到蠕滑力见式(13)。
式中:G为剪切弹性模量,Cij为蠕滑系数,可通过查表或插值获得。Kalker线性理论仅适用于小蠕滑和小自旋,在椭圆接触区处于全黏着状态时得到的轮轨之间切向力是足够精确的,但在接触区出现滑动或者局部滑动时,该模型误差较大。当轮轨接触表面因滚动产生相对转动时,可由沈氏理论[8,19]进行修正,见式(14)。
沈氏理论[8]考虑了ξz对Fx,Fy和M的影响,明显改善了V-J无自旋三维滚动接触理论模型的计算结果,与FANSTSIM 和CONTACT 的精确理论具有较好的一致性。
3) 钢轨钢安定极限计算。金学松等[8,21]提出选用钢轨的安定极限作为许用荷载更为符合轮轨相互作用的实际工况,得出椭圆接触(0<a/b<1)时安定极限qm为[8,21]:
3.2 轮轨接触力相关参数影响分析
选取弹性支撑块式无砟轨道垂向刚度和阻尼参数(其他类型无砟轨道没有落轴试验数据),列车选取CRH2型动车组,车轮为LMA磨耗型踏面,钢轨类型为60 kg/m,计算参数取值见表3。
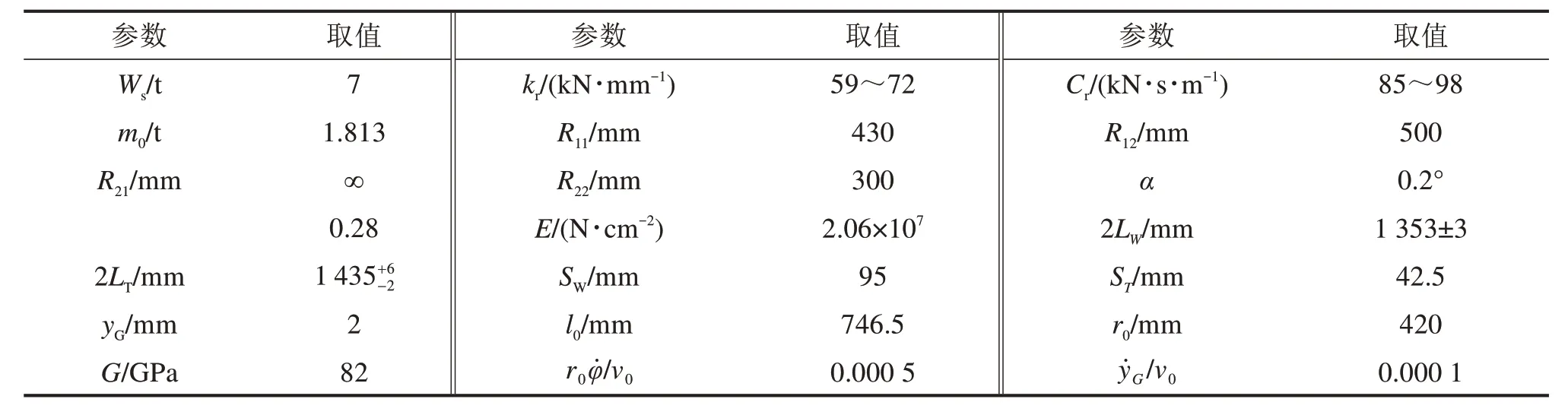
表3 轮轨接触力相关参数取值Table 3 Parameters values of wheel-rail contact force
1) 上拱矢度影响分析。钢轨上拱矢度取0.01~0.4 cm,轮轨切向力和法向应力计算结果如图5 所示。轮轨接触力随着上拱矢度的增加而增大,当上拱0.2 cm时,动轮载为21.45 t,相较平顺时增大3.1 倍,切向力为15.86 kN,增大2.1 倍,法向最大应力为1 131.6 MPa,增大1.5倍,大于安定极限值qm=942.3 MPa,钢轨上拱时最大法向应力超出安定极限值20.1%,钢轨表面丧失安定性,形成不均匀磨耗,最终可能导致钢轨波磨病害。

图5 上拱矢度影响Fig. 5 Influence of the rail uplift
2) 列车参数影响分析。分析静轮重影响时,簧下质量m0取1 813 kg,静轮重变化范围取5~10 t;分析簧下质量影响时,静轮重Ws取7 t,簧下质量变化范围取1~5 t。钢轨上拱矢度f取0.02 cm,计算结果见图6 和图7。轮轨接触力随着静轮重和簧下质量的增加而增大,静轮重每增加1 t,法向应力增大38.8 MPa,切向力增大0.87 kN;簧下质量每增加1 t,法向应力增大0.84 MPa,切向力增大0.02 kN。

图6 列车轮载影响Fig. 6 Influence of the wheel load
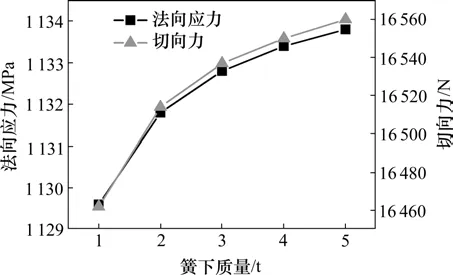
图7 列车簧下质量影响Fig. 7 Influence of train unsprung mass
3) 轨道参数影响分析。分析垂向刚度影响时,阻尼取Cr=92 kN·s/m,垂向刚度变化范围取50~250 MN/m;分析阻尼影响时,刚度取kr=58.8 MN/m,阻尼变化范围取50~250 kN·s/m。钢轨上拱矢度f取0.02 cm。计算结果见图8 和图9。轮轨接触力随着轨道垂向刚度的增加而增大,随着轨道阻尼的增大而减小,轨道垂向刚度每增加50 MN/m,法向应力增大0.87 MPa,切向力增大0.02 kN,轨道阻尼每增加50 kN·s/m,法向应力减小0.06 MPa,切向力减小0.001 kN。轨道参数相较列车参数对轮轨接触力影响小。

图8 轨道整体刚度影响Fig. 8 Influence of overall track stiffness

图9 轨道整体阻尼影响Fig. 9 Influence of the overall damping of the track
4) 高速铁路各类型列车和轨道组合对比分析。选取我国CRH380/CRH2 动车组、日本100/300 系列高速列车、英国IC125/91 型动车组、法国TVGA 动车组和德国ICE 动车组的静轴重与簧下质量,选取我国长枕埋入式、弹性支撑块式、板式无砟轨道、德国博格板式及日本新干线的轨道刚度和阻尼,见表4[22]。在对各类型列车进行对比分析时,列车与轨道类型的组合关系为:CRH 系列对应弹性支撑块式,日本100/300 系列对应新干线,英、法、德列车对应博格板;在对各类型轨道进行对比分析时,选用CRH 系列动车组。计算结果见图10和图11。

表4 各类型列车和轨道参数取值Table 4 Parameters values of various train and track
由图10 可知,德国ICE 动车组的法向应力及切向力最小,英国91/IC125 型最大,前者轮轨接触力约为后者的89.9%,可知列车质量参数对轮轨接触力影响显著。由图11 可知,德国博格板轮轨接触力最小,长枕埋入式最大,前者轮轨接触力约为后者的88.2%。德国ICE 列车和日本300 系列列车参数相同而轮轨接触力有差别的原因为德国博格板比日本板式轨道阻尼要小。

图10 各类型列车轮轨接触力对比分析Fig. 10 Comparative analysis of wheel-rail contact force of various types of trains

图11 各类型轨道轮轨接触力对比分析Fig. 11 Comparative analysis of wheel-rail contact force
4 “钢轨上拱-轮载-轮轨接触力相互作用”对钢轨波磨萌生的启示意义
4.1 钢轨上拱导致波磨萌生的机理
高速铁路钢轨上拱不平顺是导致某一类型钢轨波磨萌生的根本原因之一,胡家湾大桥钢轨上拱与波磨相伴相生提供了现场支持证据。此类型波磨萌生机理为温度应力或者扣件不良导致钢轨上拱不平顺,激励高速列车轮轨(含扣件)耦合共振,致使轮轨接触力产生周期性变动,其波动峰值超过了钢轨钢安定极限,导致钢轨表面出现周期性磨损,随之轮轨系统高频强迫振动加剧,各部件伤损加速,造成恶性循环,促使钢轨波磨的萌生与发展。简言之,钢轨上拱不平顺激发轮轨系统产生高频共振导致钢轨波磨的萌生与发展。钢轨钢安定极限值受切向力的影响极大,随着钢轨上拱不平顺引起的轮轨间切向力的增加,钢轨钢的安定极限会急剧下降,波磨发生概率将会迅速增加。另外,在钢轨上拱不平顺、无砟轨道刚度较大、动车组结构相似、列车运行速度高且相近等不利因素作用下,且当轮轨高频耦合共振冲击能量无法被无砟轨道系统阻尼完全耗散时,可导致钢轨波磨和各部件疲劳伤损迅速发展。
4.2 此类型波磨萌生应具备的条件
高速铁路哪些区段容易发生钢轨上拱从而引起此类型波磨?首先是桥上无缝线路尤其小阻力扣件地段。现场调研证实高速铁路钢轨波磨多出现于桥上直线,呈多地段非连续分布,长度大约10~15 m 不等[10]。桥上易于发生波磨的主要原因可能与小阻力扣件和桥上刚度较大有关。小阻力扣件温升幅度相较于常阻力降低了32.6%,对钢轨上拱影响极为显著。除此之外桥梁刚度较大,阻尼不足,不利于轮轨振动能量的耗散;其次是钢轨内部应力不均匀地段。如无缝线路铺设不符合规范要求或养护维修不当等原因造成钢轨内部应力不均匀地段,以及各种过渡段、道岔、变坡点等容易引起应力集中的地段。德国科隆—法兰克福高速铁路线路病害也集中发生于路桥、路隧和桥隧等过渡段轨道刚性变化部位以及无砟轨道桥上扣件型式有变化的地段[23]。因此,钢轨内部巨大压应力或者应力不均匀可能引起轮轨之间动轮载波动。当前我国现行设计规范中无砟轨道设计锁定轨温取为中间轨温,尚未考虑允许温升与温降的影响,致使设计锁定轨温偏低,导致钢轨温升幅度较大,而德国无砟轨道设计锁定轨温取值比中间轨温高3 ℃[24]。另外高速铁路长钢轨在温度力作用下的形变首先会发生于竖向(即微量上拱),然后才会横向变形,国内外无缝线路稳定性现场试验也证实了这一观点[16]。由本文计算可知极微小的钢轨上拱不平顺(如0.1 mm)就可导致动轮载加倍,并且这种上拱变形肉眼很难发现,致使钢轨波磨萌生规律隐藏在复杂的现象中,因而不容易从工程角度直觉到。类似于钢轨长波长单波上拱引起轨面多波伤损现象也同样存在于公路路面“搓板”变形中[5]。
4.3 防止或抑制此类型波磨的措施
1) 严格控制钢轨上拱不平顺是防止波磨萌生的治本性措施。首先针对我国现行规范中无砟轨道设计锁定轨温偏低的现状,在考虑允许温升与温降的影响以及钢轨强度、稳定性和断缝检算均满足要求的前提下,适当提高设计锁定轨温,通过降低温升幅度减少钢轨上拱的风险;其次扣件系统参数为抑制钢轨上拱的关键参数,扣件系统必须经常保持摩擦紧固锁定的良好状态。除此之外德国高速铁路规范规定扣件系统在65 ℃高温时各部件以及整体性能必须满足使用性能要求[25],因此建议我国也应开展扣件系统高温性能评估。另外控制钢轨上拱还应该保持钢轨内部的应力均衡以及防止出现异常的应力集中。
2) 抑制轮轨系统共振以及减小轮载变化幅值可减缓或避免钢轨波磨的萌生。在轨道方面,通过提供良好的几何形位和弹性均匀性以及足够的轮轨系统阻尼来降低动轮载;在机车车辆方面,减轻簧下质量、优化悬挂设计和减少轮径差对降低动轮载有利。另外,应该对列车参数、轨道参数和轮轨接触参数进行统一优化设计,有利于实现系统合理匹配。国外高速铁路运营经验表明,轨道的弹性和阻尼效应以及严格控制轨面不平顺对于降低轮轨动力作用是非常重要的[16]。例如日本新干线为限定轮载变化范围,把钢轨扣件的垫板刚度从90 kN/mm 减小到60 kN/mm[16]。日本新干线提速后为把轮载变化保持在提速前的水平,采用把扣件垫板刚度减少20%~30%来全面抑制轮载变化,采用把轨道不平顺减少10%来抑制特殊地点的轮载变化[16]。
3) 提高高速铁路钢轨材质强度及耐磨性能,可减缓波磨的发生与发展。改进钢轨钢的化学成分及提高纯净度,改进轧制生产工艺,提高热处理工艺质量,消除钢轨残余应力,保证出厂钢轨具有合格的平顺度精度,这些措施可提高钢轨的机械和使用性能以及钢轨钢的安定极限(安定极限主要取决于材料的屈服极限),从而抑制波磨的发生与发展。日本新干线高速高效运转的经验之一是通过提高钢轨钢的耐磨性能实现钢轨的耐久性,该指标对钢轨波磨的发生发展影响非常大[26]。德国铁路和钢铁工业协会钢轨波磨相关研究中证明经600 ℃热处理的钢轨或者先进生产工艺使内部应力特别低的钢轨,对抑制波磨的萌生有效[27]。
4) 采取预防性和修复性打磨等措施,仍然是解决高速铁路钢轨波磨问题普遍采用的有效治标措施。对于新钢轨的预防性打磨要做到完全消除钢轨表面脱碳层,并通过对打磨工艺的优化,
提高钢轨表面初始平顺性,同时充分打磨还可释放钢轨的残余应力以及均衡钢轨内部纵向应力;对于钢轨修复性打磨来说,要做到早发现早打磨,尽早消除初期波磨。为了使打磨效果能够耐久,打磨时至少要打磨到低于波谷0.05 mm,这样可以防止在波峰和波谷之间存在硬度差异[27]。
4.4 对车轮多边形发生发展机理的启示意义
“上拱-轮载-轮轨接触力相互作用”对提出车轮多边形发生发展机理具有启示意义,但所提出的机理仅仅是推测,有待进一步深入研究论证。钢轨上拱不平顺激励高速列车轮轨耦合共振,从而使轮轨接触力(包括法向和切向)产生周期性波动,并增大了轮轨相互作用力,导致周期性的车轮多边形磨损。目前已发表的关于车轮多边形的共同特征可能为上述猜想提供支持证据。郭涛等[28]通过对某高速铁路观测统计研究得出造成钢轨波磨与列车车轮多边形的原因是轮轨系统不良而诱发的耦合振动,二者具有明显的相伴相生特征。闫子权等[29]通过跟踪测试及仿真分析认为在外部激扰条件下轮轨耦合共振是产生车轮多边形和钢轨波磨的内在原因。赵国堂[30]认为车轮钢硬度比钢轨硬度小,因此车轮容易产生磨耗。
5 钢轨上拱引发波磨相关研究中的前沿问题和展望
钢轨波磨是世界铁路技术和理论研究中的热点问题和亟需解决的重大技术难题。当前的研究需要进一步基于系统科学的思想深入开展钢轨波磨多方面、多学科综合性研究,通过试验和调研获取钢轨波磨相关参数,采用日益革新的技术手段不断深化研究钢轨波磨萌生和动态发展过程。一系列前沿技术和理论问题有待探索揭示,这些问题包括但不局限于:
1) 基于系统工程思想,钢轨波磨机理研究涉及到固体接触力学、摩擦学、材料学、车辆系统动力学、轨道静力学及动力学、无缝线路理论、机械设计理论、结构稳定理论、弹塑性理论等多学科,并区分为钢轨、车轮、转向架、簧下质量、轨道类型、扣件性能、轮轨接触关系等多方面,以及经常服役于复杂运营环境条件(包括高温、低温、高湿、腐蚀、雨雪、风沙)和线路运营条件等多因素开展更为深入的波磨萌生机理和动态发展机制研究。构建高速铁路无砟轨道车轨耦合动力学模型,深入研究钢轨上拱不平顺激励与轮轨耦合振动特性之间的内在联系,进一步揭示轮轨耦合振动特性(波长、频率和幅值等)与车辆轨道结构参数和车速的映射关系,不断优化高速铁路轮轨系统各部件动力学性能匹配设计。
2) 开展与波磨萌生相关参数的试验研究,包括:各类型无砟轨道系统的整体刚度和阻尼(落轴试验),扣件系统扣压力以及高温性能适应性,钢轨蠕滑率和轮轨表面硬度,钢轨的温度压应力及钢轨上拱对轮轨振动特性的影响研究;并对钢轨波磨各影响因素进行现场调查和统计分析,包括:钢轨波磨发生地段的无缝线路稳定性相关参数,钢轨上拱长度、矢度及易发地段,钢轨特性,机车车辆类型和运营速度,钢轨波磨的总长度和波长与波幅、波磨的季节变化特征调研等。
3) 采用激光成像位移监测技术、机器视觉与图像处理、高速摄影成像技术以及高速铁路基础设施综合检测与评估成套技术等高新技术,构建实时监测技术和精准检测方法,研究高速铁路钢轨波磨发生发展的动态过程,对模型适用性进行验证,寻找轮轨耦合共振激励来源的直接证据,确定钢轨波磨的易发地段以及季节性变化机制。
6 结论
1) 建立了钢轨上拱-大幅值轮载-轮轨接触力统一模型。以CRH2型动车组和弹性支撑块式无砟轨道组合为例,计算结果表明:扣件系统参数为抑制钢轨上拱的关键参数,钢轨上拱矢度对轮轨接触力影响显著,如当钢轨上拱0.2 cm 时,动轮载为21.45 t,相较平顺时增大3.1 倍,切向力为15.86 kN,增大2.1倍,法向最大应力为11 31.6 MPa,增大1.5 倍,超出安定极限值20.1%;轮轨接触力随着静轮重和簧下质量的增加而增大,静轮重每增加1 t,法向应力增大38.8 MPa,切向力增大0.87 kN,簧下质量每增加1 t,法向应力增大0.84 MPa,切向力增大0.02 kN;轮轨接触力随着轨道垂向刚度的增加而增大,而随着轨道阻尼的增大而减小,轨道垂向刚度每增加50 MN/m,法向应力增大0.87 MPa,切向力增大0.02 kN,轨道阻尼每增加50 kN·s/m,法向应力减小0.06 MPa,切向力减小0.001 kN。
2) 系统阐释了钢轨上拱、轮载与轮轨接触力之间关联和相互作用对理解钢轨波磨萌生机理的启示意义,如钢轨上拱产生轮轨激励激发轮轨系统高频共振导致钢轨波磨的萌生与发展;此类型波磨多发生于桥上无缝线路尤其小阻力扣件地段以及钢轨内部应力较大且不均匀地段;防止或抑制此类型波磨的主要措施有严格控制钢轨上拱不平顺、减小轮轨系统共振和轮载变化幅值、提高钢轨材质强度及耐磨性能、采取预防性和修复性打磨;并对提出车轮多边形萌生机理的猜想也具有启示意义等。
