真空管道磁悬浮列车气动特性及激波效应三维研究

陈雨成，秦斌，梁习锋

(中南大学 交通运输工程学院，湖南 长沙 410075)

近年来，随着高速列车技术的飞速发展，国内外研究人员通过风洞试验和数值模拟等手段对高速列车的空气动力学特性进行了大量研究[1-2]。然而，随着传统高速列车的运行速度越来越高，可能会出现相当大的问题：空气阻力和气动噪声功率迅速增加[3-4]，导致列车能耗急剧上升。此外，横风等外部天气条件会增加列车运行稳定性的安全隐患。诸如此类问题的出现制约了列车的进一步提速，因此构建真空管道交通系统的想法应运而生。真空管道交通系统是磁悬浮列车在抽成一定真空度的管道中运行。与在标准大气压下运行的高速列车相比，真空管道交通系统具有以下优点：1) 低压管道环境支持更高的运行速度，同时显著降低运行能耗；2) 更低的气动噪声；3) 更安全的运行环境。2013 年，SpaceX 公司的MUSK[5]提出了被称为Hyperloop 的一种类似真空管道磁悬浮列车的概念性运输方式。随后TAYLOR 等[6]从可行性和经济性的角度对Hyperloop 进行了分析。BRAUN 等[7-8]对hyperloop 的吊舱进行了最小化阻力、最大化升力的外形设计，并利用数值模拟以提高其空气动力学性能。虽然对Hyperloop 的研究针对的是真空管道中长度较短的飞行器，但对真空管道高速列车的研究有一定参考价值。对于真空管道列车，研究人员对其外部流场的气动特性进行了大量的理论和数值研究。总的来说，影响真空管道列车气动性能的主要参数包括：列车速度v，管道压力P和阻塞比β(=Atrain/Atube，其中Atrain和Atube分别为列车和管道截面积)等。KIM 等[9]使用二维数值模型研究了真空管道列车在v=500~700 km/h，P=0.01~0.05 atm(1 atm=101 325 Pa)和β=0.25~0.75条件下的气动特性，得到在不同条件下v-β，β-P和P-v的关系曲线，并找到了在不同压力和阻塞比的管道内可能引起激波的临界速度。ZHANG[10]建立了一个直径为3 m 的真空管道运输系统二维数值模型，在v=50~300 km/h，P=0.001~0.1 atm 和β=0.21~0.69 的条件下对真空管道列车进行了数值模拟，并根据实用性和经济性对各种参数给出了合理的取值范围。MA 等[11]利用高温超导磁悬浮实验系统证实了列车速度、管压和阻塞比是影响真空管道列车能量损失的3个重要因素，并得出当管压和阻塞比恒定时，空气阻力是速度的二次函数。对于真空管道列车的外形设计，CHEN 等[12-14]在二维尺度上对不同头型和尾型的列车进行了数值模拟。在β=0.25~0.4 和P=1 000 Pa，CHEN 等[12-14]得出钝头形或椭圆形(2:1)的头、尾型能达到最佳的空气动力学性能。在β=0.21~0.69 和P=0.000 1~0.1 atm 时，BIBIN 等[13]得出椭圆和三角形(2:1)的头、尾型为减阻的最佳选择。对于真空管道中气流特性的研究，JIA 等[15]建立了带有压力循环管道(PRD)的真空管道列车二维数值模型。PRD 的存在可以有效降低列车头尾压差，在P=10 000 Pa，β=0.30，v=400 m/s 时可降低高达30%。此外，还讨论了管中出现的车头壅塞现象。NIU 等[16]采用二维数值模型对v=400~2 000 km/h的真空管道列车进行模拟，再现了管内冲击波在亚声速、跨声速和超声速下的产生和发展。ZHOU 等[17-18]用二维数值模型展示了真空管道列车在v=1 250 km/h时管道内弓形激波、正激波、反射激波、Lambda 激波和菱形激波等激波簇结构的产生、发展与消失的过程，还对真空管道中临界阻塞比和临界来流马赫数之间的关系进行了研究。随后，ZHOU 等[19]建立真空管道磁悬浮列车三维模型，探究了P=0.01 atm，β=0.3 的真空管道中马赫数Ma=1 的磁悬浮列车悬浮间隙对列车气动特性的影响，得出间隙减小有利于缩短正激波的形成时间。此外，张晓涵等[20-21]采用二维数值模型，胡啸等[22]采用三维数值模型，分别研究了不同气压、阻塞比和车速条件下真空管道中壅塞区的长度和激波的强度及结构变化的规律。综上所述，首先，以往对真空管道列车气动特性的研究较多使用二维数值模型，而采用三维模型对管道内部激波的产生及分布的研究较少。使用三维数值模型可以更准确地捕捉流场结构，获得比二维模型更可信的结果。其次，对于较高的来流马赫数对真空管道列车的影响研究较少。第三，较为缺乏对激波、涡流和边界层的相互作用的详细研究。因此，本文基于三维模型处理较高来流马赫数下的真空管道列车问题，重点关注尾流流场结构。本文采用数值模拟方法，再现了不同压力或来流条件下真空管道磁悬浮列车的流场分布。管道阻塞比β=0.15，压力为P∞=0.1 和0.3 atm。来流马赫数Ma∞(=v/c，其中v和c分别为流速和当地声速)设置为0.490，0.654，0.817 和0.980。本文的结构如下：首先介绍算法和真空管道磁悬浮列车模型，包括几何模型、网格及边界条件及其验证。然后分析了不同压力和来流马赫数下的数值模拟结果，包括整个流场的分布和激波在尾流中的传播。最后给出结论。

1 数值模型

1.1 几何模型

真空度管道磁悬浮列车几何模型采用基于高速磁悬浮列车EMU1的5 车编组模型，几何拓扑模型如图1 所示。磁悬浮列车由1 节头车、3 节中间车以及1 节尾车构成，头尾具有相同的流线型结构。坐标轴原点设置在头车末端中心点，x，y，z轴分别沿列车的长、宽、高方向。计算域长830 m，轨道在计算域正中间，列车头车鼻尖点距离入口200 m，尾车鼻尖点距离出口500 m。管道横截面为扇形，面积为80 m2，管道阻塞比为0.15。以上计算域尺寸为全尺寸情况，实际计算以1:8 缩比尺度进行。

图1 真空管道磁悬浮列车EMU1几何拓扑模型Fig. 1 Geometric topology model of the EMU1 vacuum tube maglev train

1.2 计算网格及边界条件

本文采用ANSYS ICEM CFD 软件的拓扑优化、多层网格加密技术、附面层网格技术与网格拉伸技术展开精细化网格划分。本文全局采用三角形网格划分，网格模型如图2所示。头、尾车网格40 mm 尺度，中车网格60 mm 尺度，流线型部分面的尺度为30 mm。考虑到尾流区复杂的流动现象，设置尾车流线型部分区域网格尺寸为10 mm。整体的加密区有3 层，尺度分别为200，400 和600 mm。共设置8 层附面层，0.3 mm 尺度。以上网格尺寸均为全尺寸情况，计算时采用1:8 缩比，模型总体网格规模约为2.1亿。

图2 计算网格示意图Fig. 2 Grid model of tube and train

本文采用ANSYS FLUENT 软件进行网格模型的流场仿真。稳态计算基于显式压力基求解方法，湍流模型选用SSTk-ω模型。针对马赫数小于1 的真空管道列车气动特性研究，采用SIMPLE 算法，王海明等[23]研究了列车首尾压差变化规律(Ma=0.35-0.71)，黄尊地等[24]分析了其气动阻力(Ma=0.16-0.82)。本文为保证运算效率，稳态计算压力-速度耦合选用SIMPLE 算法，压力采用Standard 离散格式，动量、湍动能、比耗散率均采用2阶迎风离散格式。非稳态计算以稳态流场作为初始流场，湍流模型选用LES，亚格子模型为Smagorinsky模型。压力-速度耦合选用Coupled 方法，非稳态计算时间步长取5×10-5s，共计算10 000个时间步。

由于计算来流速度较高，空气压缩效应明显，湍流模型选择Density-Based，气体采用理想气体。为模拟无穷远处的自由可压缩流动，计算域入口处采用压力远场(给定来流马赫数)边界条件，流域出口处为压力出口边界条件。隧道壁面及轨道设置为滑移壁面边界条件，其速度和来流速度一致，列车模型表面设定为固定壁面边界条件。管道内气压P∞设置为0.1 atm 和0.3 atm。设置来流马赫数Ma∞=0.490，0.654，0.817，0.980。

1.3 验证

1.3.1 数值算法验证

为了验证数值仿真算法的合理性，以翼型Rae 2822 为验证实例进行建模[25]并根据本文使用的湍流模型及边界条件进行计算，压力远场边界用于模拟无限流入的流动。图3为翼型Rae 2822的数值验证结果，其中显示了压力系数的分布以及数值模拟与实验所得压力系数的比较。选择0.74 的来流马赫数和25 000 Pa 的压力条件，可以在翼型的上表面观察到激波，如图3(a)所示。如图3(b)所示，模拟获得的结果与实验测量的结果非常吻合。

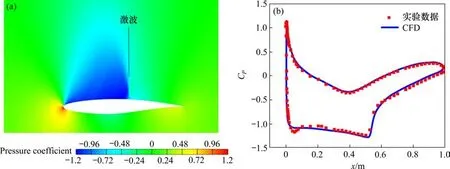
图3 翼型 Rae 2822的数值验证结果Fig. 3 Numerical verification result of Airfoil Rae 2822

此外，为了验证本文所采用的数值算法捕捉激波间断的能力，建立如图4(a)所示的数值模型，基于LI 等[26]以缩放喷管原理设计的超声速风洞试验进行数值仿真算法验证，并捕捉到了超声速来流下管道内由楔形块引起的初始斜激波与激波串。入口来流马赫数为1.85，温度为182 K。风洞试验与数值算法捕捉到的管道激波串对比如图4(b)～4(c)所示，两者流场结构基本一致，数值算法不仅捕捉到了斜激波的反射与干涉，包括激波诱导管道壁面边界层分离同样也被精确捕捉。图5比较了沿管道壁面压力系数的实验结果与数值仿真结果，两者吻合较好。因此，本文所采用的数值算法与边界条件可以精确捕捉真空管道中激波结构以及激波与边界层之间的相互干扰，具有一定的可信度。

图4 超声速风洞数值验证Fig. 4 Numerical verification of supersonic wind tunnel

图5 顶板中心线压力系数实验数据与数值模拟结果的比较Fig. 5 Comparison between experimental data and numerical simulation results of roof centerline pressure coefficient

1.3.2 网格独立性验证

为验证网格无关性，车体面网格尺寸和附面层设置保持不变，仅改变包裹列车的3层空间加密区尺寸，得到粗网格和细网格模型。从内到外，细网格空间加密区尺寸分别为100，200 和400 mm，粗网格空间加密区尺寸分别为300，600和900 mm。图6给出3套网格在10 000至20 000步的整车气动阻力系数，可知粗网格、中网格和细网格气动阻力系数分别稳定在0.295，0.273 和0.268，中网格和细网格整车阻力系数几乎重合，可认为将中网格作为计算网格模型满足网格无关性要求。另外LES 模型要求列车表面y+在1 的量级，图7 给出列车表面y+分布云图，其值均满足小于1 的条件，可知本文网格能满足LES 模型计算要求。

图6 不同网格模型整车阻力系数Fig. 6 CD of the entire train with different grid models

图7 磁悬浮列车表面y+分布云图Fig. 7 y+ distribution on the surface of the train

2 结果与讨论

2.1 整车气动特性分析

图8 展示了压力P∞=0.3 atm，来流马赫数为0.490，0.654，0.817 和0.980 对应的马赫数分布云图。取列车上方气流x=-10～25 m，y=0，z=0.7 m绘制马赫数曲线，并将列车附近流场分为5 个区域：I 区(x<0，头车上游区域)、II 区(x=0～1.64 m，头车流线型区域、收缩段)、III 区(x=1.64～14.62 m，中车段区域)、IV 区(x=14.62～16.34 m，尾车流线型区域、扩张段)和V 区(x=16.34～25 m，尾流区域)。

图8 0.3 atm压力下不同来流条件的流场马赫数云图Fig. 8 Variation of Ma of the flow field in tube at different Ma∞, P∞=0.3 atm

一般来说，流场结构可分为3 种类型，如图10(a)所示。对于类型1(Ma∞=0.490)，整个外部流场为亚声速，流速在I 区几乎保持不变，在II 区域增加，在III 区马赫数从0.591 加速到0.641，在IV 区下降，然后在V区经历小幅波动。对于类型2(Ma∞=0.654)，流场马赫数在II 区和III 区中比类型1 增长更为迅速，在IV区马赫数达到1。在尾车肩部开始出现激波，之后流场马赫数在1附近波动，然后由于膨胀波而下降。在V 区气流马赫数的振荡比类型1更剧烈，这可能导致更强的涡旋脱落。对于类型3(Ma∞>0.654)，流场在III 区中变为超声速，然后在IV 区继续加速。在尾流中，可以观察到斜激波和“X”型激波，干扰了边界层和涡流。

图10 0.3 atm压力下不同来流条件列车上方气流变化曲线Fig. 10 Changes in airflow above the train under different Ma∞, P∞ = 0.3 atm

图9 和图10(b)展示了压力系数CP分布云图及列车上方气流的压力系数曲线。对于类型1，头车流线型的前端有一个高压区。头车前部附近区域为正压区，中车和尾车及下游的流场为负压区，中车附近形成高负压区。对于类型2，头车前部附近的压力增加，正压区逐渐向后移动。对于类型3，高负压区向尾车后方移动，尾车后方形成显著的压力波动。

图9 0.3 atm压力下不同来流条件的流场压力系数云图Fig. 9 Variation of CP in tube under different Ma∞, P∞ = 0.3 atm

图11 显示了不同压力的管道中不同来流条件下列车上方气流的变化曲线。可见不同压力条件下，气流的变化趋势基本相同。从气流马赫数来看，亚声速区I，II 和III 中P∞=0.1 atm 管道气流马赫数略高于P∞=0.3 atm 管道。而在区域IV 出现超声速区的情况下，压力P∞=0.3 atm 管道气流马赫数在区域IV 和V 中高于P∞=0.1 atm 管道，波动也更为剧烈。从气流压力系数来看，总体上不同压力条件下相同来流马赫数的气流压力系数差异并不明显。可以观察到在更低真空度的P∞=0.1 atm 管道气流在区域IV和V中波动更为平缓。

图11 不同来流条件和压力下列车上方气流变化曲线Fig. 11 Changes in airflow above the train under different Ma∞ and P∞

2.2 尾流区流场结构分析

在对真空管道列车空气动力学特性的研究中，对不同来流条件下尾流区流场结构的分析具有极其重要的意义。随着来流马赫数的增加，激波对尾流区流场结构的影响逐渐增大。

图12 展示了在压力P∞=0.3 atm 的不同来流条件下尾车附近涡量的变化情况。尾车区域出现了较强烈的扰动涡量，分离流向后形成了典型的脱落尾涡结构。对于流场类型1 和2，并没有形成尾部激波。而与类型1 相比，类型2 在气流马赫数增大后尾流涡的强度相应增大。对于类型3，尾涡的脱落相对于类型1 和2 受到抑制，涡脱过程在尾流中变得更加规律。这说明激波的出现会损耗附近的扰动能量，进而干扰和削弱尾涡结构的发展和向后传递。

图12 不同来流条件的尾流涡量云图Fig. 12 Vorticity contours in the wake at different Ma∞

在来流马赫数接近1 之后，类型3 中不同来流马赫数的跨声速流场具有相似的流场马赫数分布，而压力系数呈现梯度分布，如图13 所示。从图中也可以观察到当气流通过激波位置时马赫数的骤降和压力系数的骤升。

图13 不同来流条件的尾流流场结构，l为取值线Fig. 13 Wake structure of flow field with different Ma∞, l represents the line of the value

图14 对来流马赫数为0.980条件下列车尾流区域的流场结构进行了放大展示。当超声速气流经过尾车时，尾车流线型表面形成低压区，边界层在尾车流线型端部分离，诱导产生斜激波1。斜激波1遇到管道壁面后产生反射，并与壁面以及尾流中形成的涡相互干涉后，诱导形成一道“X”型激波结构(2，3，4和5)。与二维模型相比，三维数值模型对圆柱体管道内激波结构的模拟将导致管道壁面“菱形”激波结构的入射角逐渐增大，如图15所示。

图14 尾流流场结构图Fig. 14 Wake structure behind TC

图15 尾流下游流场结构Fig. 15 Wake structure of downstream extension area

图16给出了Ma∞=0.980下的Q 判据[27]涡结构云图，可以观察到I，II，III 和IV 区管道壁面分布大量小尺度涡结构，且尾流区强度大于头车前方区域。头车流线型和尾车流线型上表面形成周期性条纹状小尺度涡结构，直至气流在头车流线型肩部或尾车流线型端部发生分离。头车底部与轨道之间的狭窄间隙受到高速气流冲击而形成了周期性的蠕虫状涡结构。尾流区两侧形成双马尾状的大量发夹涡结构向下游发展。此外，在头、尾车流线型两侧形成了平行于车体的长条状涡，这种结构类似于机翼末端的脱落涡结构。

图16 Q判据涡结构云图Fig. 16 Vortices distribution based on Q-criterion

3 结论

1) 在阻塞比β=0.15，真空度P∞=0.3 atm 的管道中：当来流马赫数Ma∞=0.490时，整个流场区域均为亚声速，没有出现激波。当Ma∞=0.654时，气流在尾车扩张段区域起点处马赫数达到1，在扩张段中围绕马赫数为1上下波动并由多个激波的影响变为亚声速。当Ma∞=0.817~0.980 时，气流在尾车扩张段区域起点处马赫数达到1，在扩张段区域继续加速，并在尾流区形成多道斜激波。当管道真空度由0.3 atm 降为0.1 atm 后，气流变化趋势与真空度降低前基本保持一致，尾流区波动更为平缓。

2) 对于Ma∞>0.654的情况，不同来流马赫数条件下流场中的气流马赫数分布相似，而压力系数呈现梯度分布。随着尾车附近出现超声速区，将产生一系列斜激波和“X”型激波等结构。由于激波、涡流和边界层的相互影响，激波和涡出现相互干扰与融合现象。研究成果能为真空管道列车不同来流速度和不同真空度情况尾流激波抑制以及气动阻力优化设计提供工程指导。