高速铁路梁桥建模参数敏感性分析

2023-03-29胡章亮魏标蒋丽忠李姗姗

铁道科学与工程学报 2023年2期

胡章亮，魏标，蒋丽忠，李姗姗

(1. 中南大学土木工程学院，湖南长沙 410075；2. 高速铁路建造技术国家工程研究中心，湖南长沙 410075)

建立动力有限元模型是获得桥梁结构地震响应、计算构件损伤概率和评估结构抗震性能的重要手段。由于结构材料、几何尺寸以及边界条件存在固有的随机性，导致桥梁模型也不再是确定的。因此，必须在桥梁模型特别是进行概率地震需求分析模型中，指出影响构件地震响应的不确定性建模参数。已有研究评估了桥梁模型中各种不确定性对构件地震响应的敏感性。NIELSON[1]针对混凝土简支梁桥、简支钢桥、多跨混凝土连续梁桥和连续钢桥，通过因素筛选试验考虑了15 种建模不确定性因素的影响。PADGETT 等[2]在此基础上通过分式析因设计确定了显著影响加固改造公路梁桥地震响应的建模重要参数以及减震装置参数。吴文朋[3]将建模不确定性参数细化为结构、材料和边界层次，考虑了26 种不确定性参数建立了一座4×30 m 公路连续梁桥有限元模型，通过基于条带法的敏感性分析方法筛选出13 种重要不确定性参数。于晓辉等[4]结合一次二阶矩法和增量动力分析方法，发现不确定性参数对混凝土框架结构抗倒塌能力的对数标准差有放大效应。宋帅[5]采用Tornado 图进行了建模随机参数对一座三跨简支T 梁响应影响的重要性识别，PORTER 等[6]也运用该法开展建筑结构易损性和损失估计敏感性分析。JIANG 等[7]在建立高速铁路连续梁桥时考虑了8 种桥梁结构建模参数，评估了桥墩与支座的损伤。魏标等[8]研究了高速铁路桥梁数值模型精细化程度对结构损伤概率的影响。然而，上述不确定建模参数的研究主要依托于公路梁桥或建筑结构，仍然缺乏建模重要性参数对高速铁路梁桥影响的全面理解。概率地震需求分析中的高速铁路桥梁动力计算有限元模型涉及到诸多不确定性参数，悉数考虑所有不确定性参数使得建模过程极为繁杂，而且所有不确定性参数对计算结果的贡献不一，因此识别出重要建模参数，实现有效建模的同时确保模型计算结果的精确度显得尤为必要。因此，本文首先以高速铁路梁桥中的简支梁桥和连续梁桥为例，基于OpenSees 平台分别建立动力计算有限元模型；其次，统计相关建模不确定性参数的分布规律，采用两水平分式析因设计将不确定性参数融入有限元模型中；最后，通过方差分析筛选出显著影响高速铁路梁桥地震响应的建模参数，并评估建模参数不确定性在PSDA中的传递性。

1 算例桥梁

1.1 布局及模型

选择CRTSⅡ型高速铁路无砟轨道板的3×32 m双线简支梁桥和48 m+80 m+48 m 双线连续梁桥为工程背景，如图1 所示。主梁采用单箱单室的C50混凝土截面，上铺设C30混凝土底座板和C55混凝土轨道板；主梁与底座板间填充两布一膜的滑动层材料，底座板与轨道板之间通过CA 砂浆层连接，WJ-8C 型扣件固定于轨道板上并约束CHN60型钢轨。简支梁桥布置13.5 m 高矩形桥墩，通过12 根直径1.2 m 的圆形桩构成群桩基础支撑。矩形截面的连续梁桥墩高13 m，边墩群桩基础为16 根1.5 m 直径的圆形桩，中墩群桩基础由20 根直径1.5 m 的圆形桩构成。2 种桥型均布置球型钢支座，连续梁桥2号墩顶设置纵向固定支座。

基于OpenSees 建立2 种高速铁路梁桥的动力计算有限元模型，见图1。采用弹性梁柱单元模拟主梁、底座板、轨道板和钢轨；轨道间的连接件如滑动层、CA 层和扣件以及支座采用零长度单元模拟，其力学参数见表1[9-11]。桥墩采用非线性梁柱单元模拟，3 个平动和转动弹簧用来反映桩与土之间的相互作用。

表1 轨道连接件力学参数Table 1 Mechanical parameters of track connecting components

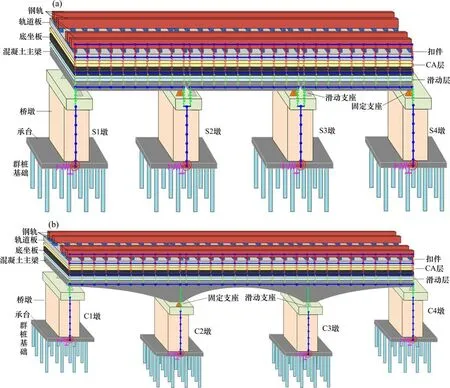
图1 高速铁路梁桥示意图Fig. 1 Schematic diagram of HRGB

1.2 地震动输入

地震波包含峰值、频谱和持时三要素，每一要素均影响结构在地震作用下的响应。即使具有相同地面峰值加速度的地震波，也会因频谱和持时的差异导致计算结果迥异，更何况是来源不同场地记录的地震波。为避免由于地震波的随机性增加问题分析的复杂程度，依据土层剪切波速从PEER 强震数据库中选择4 类场地共12 条实际地震波：震级M范围为5.90～7.28，涉及强震级(M≥6.50)和弱震级((M<6.50))；震中距R为7.57～94.48 km，涵盖了近场和远场地震动，所选地震波的详细信息如表2 所示。对原始地震波的峰值地面速度(PGV)进行标准化处理，是消除震源、断层、震级、震中距和场地属性差异性的一种简单方法，但该法并不会降低整个地震波库的强度水平，仍然保持波与波之间固有的特性[12]。表2列出12条原始地震波水平分量对应的PGV，根据式(1)可以计算得到每条地震波标准化后的系数NMi，见表2。将各地震波的PGV 乘以相应的NMi即可实现标准化处理，标准化后的各地震波的加速度反应谱曲线见图2。

图2 标准化后12条地震波加速度反应谱曲线(η=0.05)Fig. 2 Acceleration response spectrum curves of 12 seismic waves after normalization (η=0.05)

表2 4类场地地震动波Table 2 Seismic waves of four types of sites

式中：NMi为每条地震波标准化的系数；PGVPEER，i代表每条地震波的PGV，通过地震波的2条水平分量的算数平方根计算获得；Median(PGVPEER，i)为12条地震波的平均PGV。

1.3 工程需求参数

工程需求参数(EDP)的选取应能体现结构使用功能和结构安全性，针对高速铁路梁桥，分别选择桥墩保护层混凝土应变，支座、滑动层、CA 层和扣件位移共5类构件作为结构响应的代表，列在表3中。

表3 工程需求参数(EDP)Table 3 Engineering demand parameters(EDP)

2 建模不确定性参数统计

造成桥梁模型不确定性的参数很多，本文借鉴已有研究成果，剔除了部分对结构损伤概率几乎没有影响的建模参数后统计如下高速铁路梁桥建模过程中的典型不确定性参数。在建立高速铁路梁桥有限元模型中，二期恒载的简化计算以及对主梁变截面的模糊处理，造成模拟的截面尺寸与实际存在偏差，均导致结构重量存在不确定性。本文采用TAVARES 等[13]的研究成果，假定高速铁路梁桥中混凝土材料密度调整系数服从U(0.9, 1.1)的均匀分布。混凝土桥墩建模时常离散为混凝土纤维以及钢筋纤维。在OpenSees 中采用Mander 模型模拟混凝土材料，涉及到混凝土弹性模量、峰值压应变和极限压应变；采用各向同性硬化的应力-应变模型模拟纵筋，控制参数有钢筋的弹性模量和屈服强度。沿用既往文献的统计分布，假定混凝土抗压强度及其应变均服从对数正态分布，且变异系数为0.127；假定混凝土弹性模量，变异系数为0.08[14-15]。根据邹中权[16]统计结果，钢筋屈服强度采取变异系数为0.07 的对数正态分布考虑其不确定性。PANG 等[17]建议钢筋弹性模量服从对数正态分布，变异系数取0.05。混凝土保护层厚度的变异系数分别取值为0.05[3]。阻尼比直接影响地震作用下的动力响应计算结果，BAVIRISETTY等[18]的研究发现，结构的阻尼比服从均值0.05，变异系数为0.28 的正态分布。支座的摩擦因数关联支座的初始刚度，PAN等[15]认为支座摩擦因数服从均匀分布。ELLEN[19]假定支座的初始刚度服从均匀分布，记为U(0.8,1.2)，滑动层、CA 砂浆层和扣件作为连接构件，因缺乏实际统计资料，因此其初始刚度的变化假定同支座初始刚度分布一致。在计算群桩基础弹簧刚度时，NIELSON[1]将桩基础的刚度按均匀分布考虑，记为U(0.5,1.5)。此外，地震波的加载方向直接影响结构的纵、横桥向地震响应，对于具有耦合效应的结构，纵(横)桥向地震动的输入往往还会引起构件横(纵)桥向的响应变化[9]。因此，这里地震波分为沿纵桥向和横桥向加载。

综上，根据既有文献，整理高速铁路梁桥中15 种典型不确定性建模参数的分布和取值于表4。表中简支梁桥和连续梁桥结构中桩基础刚度详见文献[10]，其余参数取值和分布二者均相同。

3 分式析因设计

将多种不确定性参数悉数考虑到有限元模型中通常采用拉丁超立方抽样法、条带法[3]和一次二阶矩法[4]，但上述方法均存在诸多缺陷，因此，这里引入试验设计中的析因设计法到桥梁结构建模参数敏感性分析中来。析因设计法也称全因子设计法，通常为两水平全因子设计，是将全部试验因素的2 个水平进行组合实施2 次及以上的独立重复试验，可同时监测到全部因素的效应，该方法既能反映每个因素的主效应，又能检测到各因素之间的交互效应。针对本例高速铁路梁桥，考虑15种建模不确定性参数，将每个建模参数设定为2个水平，即低水平(5%分位值)和高水平(95%分位值)，各因素两水平值列在表4 中。若按照全因素设计，试验次数需要215=32 768，这显然是一个庞大的试验次数，采用全因素设计开展多种梁桥的敏感性分析并不可取。若假设因素间高阶交互作用可以忽略不计，则运行部分析因实验就有可能很好地估计因素的主效应和因素之间的低阶交互作用，即为分式析因设计。两水平分式析因设计的符号记为：

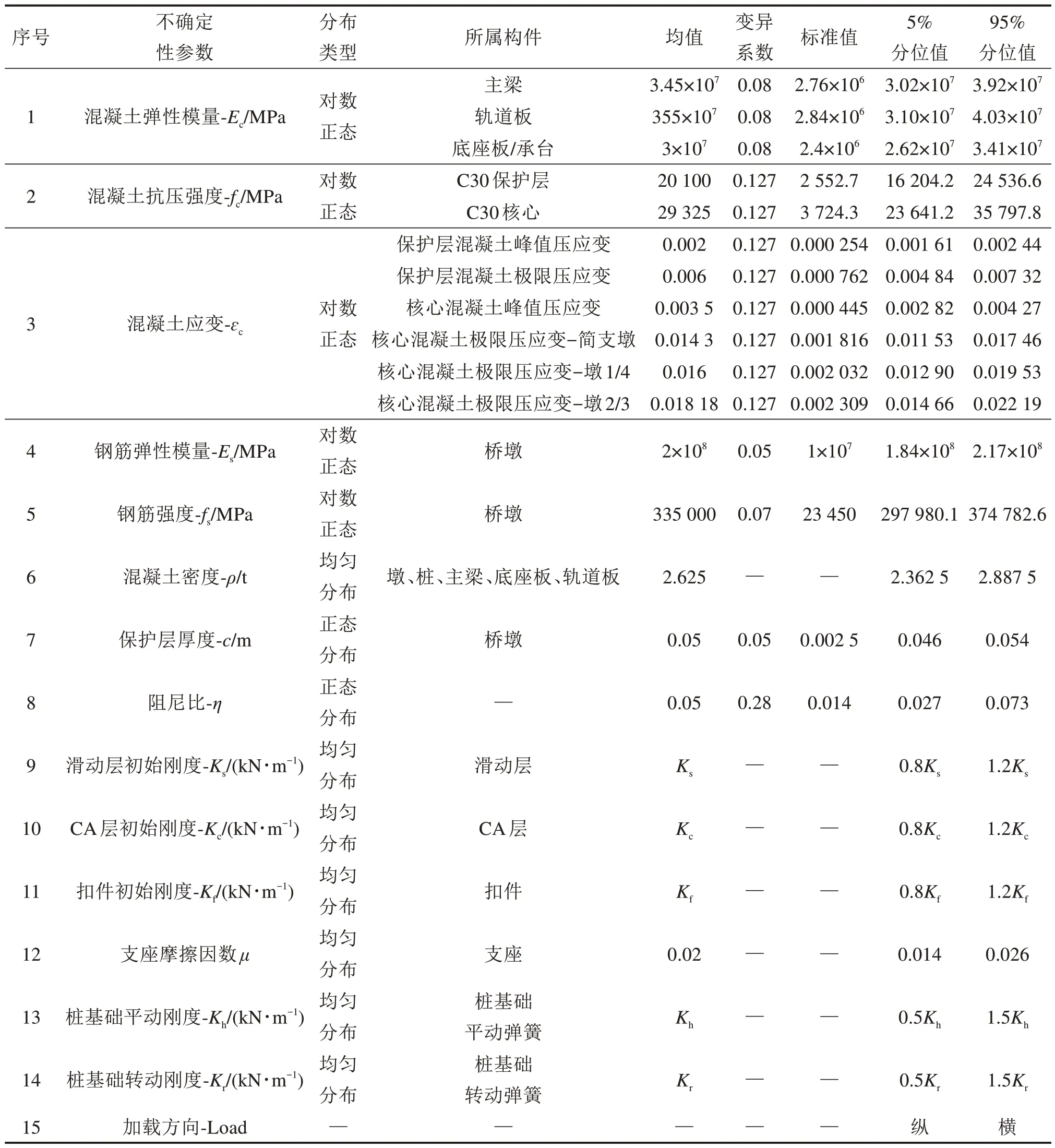
表4 高速铁路梁桥不确定性建模参数汇总Table 4 Summary of uncertain modeling parameters of HRGB

式中：2代表每个因素的水平数；k代表因素个数；2-p为分式大小；2k-p为试验次数；R代表分辨度。

在忽略3阶及以上交互效应的情况下，所选用分辨度为Ⅳ的分式析因设计可以使各因子主效应之间以及主效应和2阶交互效应之间没有别名。因此，针对上述15 种因素两水平的分式析因设计，选取分辨度为Ⅳ，利用Minitab 软件共生成了32 次试验，得到考虑所有因素和水平的32 次析因设计如表5所示。

4 敏感性分析结果

根据表5设计的两水平分式析因设计表，共需建立32 个高速铁路梁桥动力计算有限元模型，每一个模型涵盖了15 种建模不确定性参数。输入4类场地12 条地震波，累计进行384 次非线性时程分析，每一运行工况取12 条地震波计算结果的平均值作为构件的最终响应。

表5 析因设计分析Table 5 Factorial design analysis table

为评估每个构件响应对建模参数变化的敏感性，还需对计算结果进行方差分析。方差分析的具体步骤如下：1) 进行方差齐性检验；2) 计算总变异和离散变异的平方和与自由度；3) 列出方差分析表，计算显著性水平p值，检验因素的重要性。更多的统计分析表明，越小的p值表明该因素的效应越显著，p值通常可取0.01和0.05，而当p<0.05时，已具有足够的证据拒绝原假设并认为该因素的效应显著，因此，本文认为各不确定性参数计算的p值小于0.05意味着该参数的改变影响显著。

4.1 高速铁路简支梁桥

考虑了各因素的主效应和两因素之间的交互效应，由方差分析计算得到了15 种建模不确定性参数对高速铁路简支梁桥动力响应影响的p值结果，如表6所示。从表中可以看出，地震波加载方向这一参数对于所有构件响应进行方差分析得到的p值均小于0.05，由此说明，地震波加载方向是建模过程中最重要的参数。此外，混凝土密度、阻尼比以及支座摩擦因数这3 个参数也较为重要，因为它们至少对应8 个结构响应的方差分析p值小于0.05。值得注意的是，存在6 个构件的响应对滑动层初始刚度的不确定性较为敏感，这是因为，轨道结构和主梁之间的连接是通过纵桥向连续的滑动层来实现，轨道结构的约束使得原本3个独立的简支梁桥结构变成了一个整体，改变了桥梁-轨道结构的质量和刚度。滑动层刚度的变化直接决定轨道对桥梁结构约束的强弱，进而影响到整个结构的动力特性和在地震作用下的响应。

实际上，各建模参数对构件响应的影响并非是独立的，表6 显示混凝土弹性模量(Ec)与其抗压强度(fc)和混凝土弹性模量(Ec)与钢筋屈服强度(fs)交互作用显著，并且均对至少6个构件响应敏感。进一步通过方差分析还可以获得参数主效应及其2阶交互作用的效应值E，进而计算其贡献率C(式(3))，判断Ec，fc和fs的主效应及其交互作用的贡献程度。

依据表6，选取具有显著影响的参数如ρ，η，Ks，μ和Load 以及Ec，fc和fs，计算其主效应以及Ec，fc和fs2 阶交互作用的效应值和贡献率。表7 仅列出受Ec与fc和Ec与fs交互作用共同影响的工程需求参数的效应估计值和贡献率。

根据表7，Ec和fc主效应及其交互作用Ec*fc对εx-s 和Δsx-s 的拮抗作用贡献率分别为31.06%和21.99%，对δfx-s 和Δfy-s 的协同贡献率分别达19.03%和9.09%；Ec和fs主效应及其交互作用Ec*fs对Δsx-s 和Δfy-s 的拮抗贡献率分别达21.84% 和9.09%，对δfx-s 和Δfy-s 的协同贡献率较低，最高仅为5.06%。这说明交互作用Ec*fc和Ec*fs对简支梁桥工程需求参数的拮抗作用大于协同作用，且交互作用Ec*fc的影响贡献率更大，意味着建立高速铁路简支梁桥模型时不可忽略。当选择至少影响6个构件的响应时(p<0.05)能涵盖桥梁和轨道结构的响应，故以此为重要建模参数筛选的依据，则在建立高速铁路简支梁桥时不可忽略的建模参数包括：地震波加载方向、结构阻尼比、混凝土密度、支座摩擦因数和滑动层初始刚度；考虑参数间2阶交互作用时还应包括混凝土的弹性模量及其抗压强度。

表7 重要建模参数对简支梁桥工程需求参数影响的贡献率Table 7 Contribution rates of important modelling parameters to the EDPs of simply supported bridge

4.2 高速铁路连续梁桥

表8 列出了15 种建模不确定性参数对高速铁路连续梁桥影响的方差分析p值结果，表中考虑了因素的主效应和两因素之间的交互效应。从表8可以看出，除滑动层纵桥向位移外，地震波加载方向对应其他11种响应计算所得p值均小于0.05，可认为是最重要的建模参数。方差分析显示，结构的阻尼比、混凝土密度和支座的摩擦因数对应大部分构件的p值小于0.05，意味着这些建模参数在建立连续梁桥模型中贡献显著。轨道结构连接件的刚度不确定性只影响相应构件的响应，如滑动层刚度的变化只显著控制滑动层的纵、横桥向位移，而对CA 层和扣件的位移没有任何影响。这是因为，案例选择的三跨连续梁桥有别于三跨简支梁桥，其桥梁结构本身是延续的，刚度明显较大，即使附加轨道结构的约束，对其动力特性的改变也较小，这从结构动力特性分析的结果也可以看出[10]，因此，轨道结构连接件的刚度变化对整个轨道-桥梁整体的影响很小，仅影响连接件本身的响应。

表8也体现了混凝土弹性模量与其抗压强度和混凝土弹性模量与钢筋屈服强度交互作用显著，并且均对至少6 个构件响应敏感。类似于简支梁桥，选取有显著影响的参数如ρ，η，Kh，μ和Load以及Ec，fc和fs，计算其主效应以及Ec，fc和fs2 阶交互作用的效应值和贡献率，如表9所示。从表中可以看出，Ec和fc主效应及其交互作用Ec*fc对δfx-c的拮抗作用贡献率为24.10%，对εy-c，Δsy-c 和Δfx-c的协同贡献率分别达11.27%，17.44%和11.12%；Ec和fs主效应及其交互作用Ec*fs对δfx-c和Δfx-c的拮抗贡献率分别为8.7%和11.11%，对εy-c 和Δsy-c 的协同贡献率较低，最高仅为4.65%。类似于简支梁桥，交互作用Ec*fc对连续梁桥工程需求参数的影响贡献率高于交互作用Ec*fs。仍以至少影响6 种响应的参数(p<0.05)为重要建模参数的筛选标准，在建立高速铁路连续梁桥时仅考虑主效应的建模参数有地震波加载方向、结构阻尼比、混凝土密度、支座摩擦因数和桩基础的平动刚度；考虑参数之间的2阶交互作用时，混凝土的弹性模量及其抗压强度的不确定性不可忽略。

表8 15 种不确定因素对高速铁路连续梁桥地震响应影响的p值检验(0.05)Table 8 p-value test for the effect of 15 modeling parameters on the seismic response of continuous girder bridges (0.05)

表9 重要建模参数对连续梁桥工程需求参数影响的贡献率Table 9 Contribution rates of important modelling parameters to the EDPs of continuous bridge

5 考虑建模参数不确定性的概率地震需求分析

为进一步评估建模参数不确定性对PSDA 的传递影响效果，通过拉丁超立方抽样将建模参数不确定性考虑到模型中，建立如下计算工况：不考虑建模参数不确定性(所有建模参数取均值，记为Mean)、考虑所有建模参数不确定性(All)和考虑重要建模参数不确定性(Important)，选取文献[20]中80条实际地震波进行非线性时程分析并记录构件响应，对构件响应和地震动强度指标(IM)实施概率地震需求分析(PSDA)。通常假定响应与IM 之间服从对数线性关系，因此将二者取对数后进行线性回归，获得响应与IM 之间的数学关系，实现依据IM可准确预测响应的目标，此过程称为PSDA。仅以高速铁路简支梁桥为例，εx-s 和Δsx-s 的PSDA 结果如图3 所示，图3 中S*为高速铁路梁桥最优IM[10]。理论上考虑所有建模参数不确定性得到的PSDA 结果是最准确的，图3表明考虑所有建模参数不确定性得到的响应-IM 拟合结果与不考虑建模参数不确定性的拟合结果有明显的差异，从拟合表达式可看出，前者拟合得的斜率高于后者，而2种工况拟合得到的截距相差不大，由此表明当IM 大小相同时，采用不考虑建模参数不确定性的模型预测得到的构件响应值将会低于考虑建模参数不确定性的模型预测值。此外，考虑重要和全部建模参数不确定性得到的响应-IM 拟合结果基本一致，表明采用考虑重要建模参数不确定性的模型即可准确地预测构件响应，进而可实现获得准确地震易损性评估结果的同时避免了建立考虑所有建模参数不确定性模型的繁琐过程。