铁路列车-轨道-基础结构动力相互作用统一分析Part Ⅱ:混凝土车致疲劳损伤与空时演化
2023-03-29徐磊余志武
徐磊,余志武
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 高速铁路建造技术国家工程研究中心,湖南 长沙 410075)
目前,铁路列车-轨道-基础结构(Train-tracksubstructure,简称为TTS)系统动力学模拟与分析,以弹性动力学为主,用于铁路列车、线路结构系统建造阶段的动力设计与评估。然而,在铁路线路进入长期服役阶段后,列车在线路上的运行,将形成列车、轨道及基础结构三者的空间耦合振动,使结构材料呈现应力/应变的时变性,出现疲劳载荷。而在列车循环作用下,铁路工程结构的循环荷载效应加剧,容易导致混凝土结构车致疲劳损伤,随着损伤的不断累积,将出现混凝土裂纹甚至断裂,影响铁路工程结构的长期服役性能及安全。高速铁路无砟轨道结构中的轨道板、自密实混凝土填充层和底座板等属混凝土类材料,砂浆层为黏弹性材料,开展无砟轨道混凝土结构疲劳损伤动力演化研究,涉及系统不同材料疲劳损伤本构、系统动力状态空间耦合和时域演化等层面的综合研究。目前,国内外学者在混凝土疲劳损伤本构和铁路系统动力学方面开展了卓有成效的系统性研究,理论方法日臻成熟。然而,将轨道结构材料疲劳损伤和车辆-轨道系统相互作用在铁路大系统层面进行统一研究的工作方兴未艾,徐桂弘等[1]提出了基于试验分析的“轨道板-CA 砂浆-支承层”模型试件疲劳累积损伤的演化方程;陈醉等[2]开展了列车轮载作用下CRTS II 型轨道板的疲劳特性及板体自振对疲劳寿命的影响分析;王青等[3]采用静力等效法开展了CRTS II 型板在列车往复荷载作用下的疲劳力学性能分析;基于类似的方法,周凌宇等[4]对双线列车荷载作用下结构体系各层材料疲劳损伤劣化分析,揭示了简支梁桥上CRTS II 型板的经时力学性能演化规律;基于ABAQUS商用有限元软件,朱胜阳等[5]开展了车辆和温度作用下无砟轨道结构伤损行为及动力学影响研究,但主要涉及结构层间的耦合及损伤演变分析。然而,现有工作较少从铁路列车-轨道-基础结构系统耦合振动角度,模拟与揭示无砟轨道混凝土结构在疲劳寿命期内的损伤演化过程。本文基于铁路列车-轨道-基础结构系统统一分析模型,引入无砟轨道混凝土类、黏弹性类材料的疲劳损伤本构关系,建立列车循环作用下无砟轨道混凝土结构疲劳损伤动力演化计算模型,较为系统地开展无砟轨道混凝土结构疲劳损伤动力演化研究。
1 混凝土车致疲劳损伤与空时演化分析的基本框架
本文暂不考虑环境荷载作用,且主要聚焦轨道结构中混凝土类材料的疲劳损伤演化,视列车循环作用下的TTS 系统空间振动与时域演化为动力学时变统一过程,时变性体现在混凝土结构的疲劳损伤将随着列车移动而不断更新,统一性体现在不同次列车循环作用下上一次结构疲劳损伤作为下一次的初始条件(见图1),换言之,TTS 系统中混凝土结构的疲劳损伤过程为TTS 系统动力学统一模型下的空时演化过程。

图1 混凝土结构疲劳损伤的空时演化过程Fig. 1 Spatial-temporal evolution process of fatigue damage in concrete structures
分析步骤如下:
1) 采用有限单元法将混凝土结构空间离散化,建立并求解TTS 系统动力学运动方程,获取结构在第n次列车循环、第tk时刻、单元高斯点(xi,yj)处子单元的应变为
式中:下标Q 表示混凝土结构类型;B为单元应变矩阵;X为单元振动位移向量;Φ(xi,yj)为单元自由度向量。
进一步地,可将混凝土结构单元的应变矩阵化为
2) 引入混凝土疲劳损伤本构:σQ(tk|n) =H[εQ(tk|n)],其中:H[ ·]为疲劳损伤本构的表征函数集。根据相邻时刻单元高斯点应变εQ(tk-2~k|n)的变化情况,判断单元疲劳荷载的加卸载状态,结合单元应力σQ(tk|n),确定单元损伤变量dQ(tk|n)及弹性模量更新值EQ(tk|n)。
3) 更新tk时刻混凝土结构刚度矩阵,重组TTS系统动力学刚度矩阵方程,重复步骤1~2,直至完成第n次列车循环作用。根据混凝土结构历史最大损伤矩阵DQ(n),确定第n+1次列车循环作用时的混凝土结构初始刚度矩阵。
4) 重复步骤1~3,直至混凝土结构最大损伤值大于阈值,终止疲劳损伤演化计算。
综上,可构建TTS 系统混凝土车致疲劳损伤与空时演化分析的基本框架如下。
2 混凝土结构车致疲劳损伤计算及表征
本文主要考虑无砟轨道中混凝土和砂浆类结构(如:轨道板、砂浆层等)的累积疲劳损伤,并用动力学刚度矩阵表征混凝土损伤演化状态,其中:采用中南大学余志武课题组开发的混凝土材料和砂浆层的疲劳损伤本构模型[6],简述如下。
2.1 疲劳损伤模型
2.1.1 混凝土疲劳损伤本构模型
在拉伸疲劳荷载作用下,混凝土应力-应变曲线按下列公式计算:
式中:n为荷载加载次数;N为疲劳寿命;Dt,n为经历n次加载时混凝土疲劳损伤变量;D0t,n为经历n次加载时混凝土疲劳受拉归一化损伤变量;At,1,At,2和At,3为混凝土受拉损伤演化相关参数;σmax和σmin分别为疲劳荷载的应力上、下限值;ftk为混凝土单轴抗拉强度标准值;S为混凝土应力水平;εt,k为与单轴抗拉强度标准值对应的混凝土峰值拉应变。

图2 铁路工程结构混凝土车致疲劳损伤与空时演化分析框架Fig. 2 A framework for the fatigue damage and spatial-temporal evolution analysis of concrete structure induced by a moving train in railway engineering structures
混凝土受拉疲劳加载过程中,混凝土卸载应力路径可按下列公式计算:
式中:Et,n为疲劳受拉混凝土卸载弹性模量;εt,z为疲劳受拉混凝土卸载至零应力点时的残余应变。
经过疲劳加载后,混凝土静力单轴受拉应力-应变曲线建议按下列公式计算:
其中:Dft,k=(1-S)D0t,n
式中:σpt,n为经过n次加载后,混凝土单轴受拉应力;Dft,k为经历n次加载后,混凝土抗拉强度劣化系数;Dpt为以(ε-εt,z)为自变量的混凝土单轴受拉损伤变量。
经过疲劳加载后,混凝土受拉残余应变建议按下列公式计算:
与混凝土受压损伤演化相关应力-应变曲线、残余应变等计算公式可参考文献[6]。
2.1.2 砂浆黏弹性-损伤本构模型
基于砂浆疲劳随机黏弹性-损伤本构模型,疲劳荷载作用下的砂浆应力-应变曲线如下:
式中:上标“+”和-”分别为受压和受拉状态;Dml为损伤变量;Eml,0为砂浆的疲劳动弹性模量。
第n次疲劳加载的疲劳损伤变量用下式计算:
疲劳加载弹性模量和疲劳寿命计算公式见文献[6]。
2.2 混凝土结构的疲劳损伤表征及矩阵更新
在TTS 统一分析模型中,混凝土结构主要由板单元及空间等参单元模拟[7],其损伤刚度矩阵及更新方法如下。
2.2.1 混凝土板刚度矩阵
考虑到结构动力性能演化主要由材料弹性模量退化引起,混凝土板单元的刚度矩阵更新可表示为
式中:W为板单元的弹性变形;Ex和Ey分别为板单元的纵向和横向弹性模量;μ为泊松比;G为剪切模量;Np和Xp分别为板单元的形函数和位移向量;x和y分别为纵、横向局部坐标;ls和lw为板单元纵、横向长度;Ψx和Ψy为纵横向划分单元集合。
2.2.2 混凝土实体刚度矩阵
以8节点空间等参单元为例,混凝土空间实体的单元刚度矩阵更新可表示为
式中:Ex,Ey和Ez分别为空间等参单元的纵、横和垂向弹性模量;μs为泊松比;Ψx,Ψy和Ψz为纵、横和垂向划分单元集合。
本文模型中砂浆层采用实体单元模拟,且仅考虑其垂向应力幅引起的疲劳。根据文献[6],第n次加载的疲劳弹性模量为
结合式(9),砂浆层疲劳弹性模量可由下式计
式中:͂为疲劳动力计算中的循环跳跃次数;Eml,0为砂浆层初始疲劳动弹性模量。
将式(13)中的Ez,n代入式(11),即可获得砂浆层的疲劳损伤刚度矩阵。
2.3 损伤矩阵更新
混凝土结构的疲劳损伤刚度矩阵具有时变性,可采用循环计算方法[8],根据列车时变位置,将轨道-基础结构系统矩阵的前、后相应边界进行空间截断,以提高计算效率。混凝土结构损伤刚度矩阵可用下式更新为
式中:ti表示第i时间步对应的时刻为损伤矩阵对应的全局自由度编号;Kα为具有损伤矩阵的全局矩阵;为初始完好矩阵;Kp(ti)和Kd(ti)为截断区段的完好矩阵和时变损伤矩阵。
2.4 疲劳残余变形的空间几何映射
式中:Krs为钢轨-轨道板耦合刚度矩阵;hc为砂浆层的厚度;Frs为轨道板受到的附加力,Frs=Krsc(Φrs,Φc)(hcεΦc);Krsc为钢轨-轨道板-砂浆层耦合刚度矩阵;Φrs为钢轨-轨道板自由度;Φc为砂浆层自由度。
3 数值分析
本节拟从试验结果对比、结构疲劳损伤空间分布及演化分析角度,以CRTS II 型板为研究对象,阐明混凝土车致疲劳损伤与空时演化分析方法的可行性。
3.1 与试验结果对比分析
文献[9]中针对CA 砂浆材料开展了等幅压缩疲劳试验,试验每组应力水平取3 个试件进行试验,疲劳荷载上限分别为Fmax=0.6fc,0.65fc,0.75fc,0.85fc疲劳荷载下限恒定为Fmin=0.05fc。每个CA 砂浆试件在轴向和横向对称位置分别粘贴4 个和2 个应变片,采用应变片和LVDT线性位移计进行相关数据的量测,见图3。

图3 CRTS II型CA砂浆等幅压缩疲劳试验加载与测量装置[7]Fig. 3 Loading and measuring device for constant amplitude compression fatigue test of CRTS-II CA mortar
将本文模型计算获得的CA 砂浆疲劳损伤演化过程与试验结果进行对比分析,见图4。

图4 CA砂浆疲劳演化行为的数值与试验结果对比Fig. 4 Comparison of numerical and experimental results on fatigue evolution behavior of CA mortar
从图4可知,在演化趋势上,本文模型算出的结果基本与试验结果基本一致,均呈现CA 砂浆疲劳损伤的“三阶段”(先加快,再逐渐增长,后急剧增加)发展特性。因为荷载形式不同,本文采用车辆-轨道动力相互作用作为砂浆损伤的荷载源,而试验采用不同应力水平(0.60,0.65,0.75和0.85)的等幅值荷载,且显著大于一般列车荷载下砂浆所承受的应力水平,故而疲劳应变幅值要大于本文计算结果。
3.2 列车作用下混凝土结构损伤空间分布特征
图5给出了路基、桥梁和隧道基础支承下轨道板底部纵、横向受拉损伤和CA 砂浆拉、压损伤分布。
从图5(a)可知,轨道板以底部纵向受拉损伤为主,不同基础结构形式对轨道板纵向受拉损伤影响十分显著,随着基础支承刚度的增大:路基<隧道<桥梁,轨道板底部纵向受拉损伤逐渐减小,路、桥、隧上损伤最大值分别为0.083 6,0.010 1和0.032 3;相较而言,轨道板底部横向受拉损伤受基础支承形式影响较小,见图5(b)。
从图5(c)和5(d)可知,CA 砂浆的受压损伤要大于其受拉损伤;不同的下部基础支承结构对CA砂浆的拉、压损伤分布影响较大,其中:在路基支承条件下,CA 砂浆板端受拉最为显著,且板角位置的损伤最大,其次为隧道支承,桥梁支承下的板端CA 砂浆损伤不再显著;此外,轨下胶垫位置的砂浆拉、压损伤均较大。显然,不同的基础支承结构对CA 砂浆的损伤分布影响较大,且具有明显的空间特异性。

图5 轨道板和CA砂浆疲劳损伤空间分布Fig. 5 Spatial distribution of fatigue damage of track slab and CA mortar
3.3 列车循环作用下混凝土结构损伤演化及响应分析
图6 给出了轨道板和CA 砂浆在列车循环作用下损伤值Dt和Dml演化过程。
从图6 可知,列车循环作用下的轨道板和CA砂浆损伤演化过程存在显著差异,由于轨道板采用预应力板,其受拉疲劳损伤显著降低,损伤发展速率较为缓慢;而砂浆层的疲劳损伤发展速率明显较快,是在混凝土板-砂浆组合结构中的薄弱层。此外,受路、桥、隧下部基础结构的影响,轨道板和CA 砂浆的损伤程度有明显差别,例如:在路基支承条件下,轨道板纵向拉应变较大,其疲劳损伤值要大于桥隧上的轨道板损伤值,而CA砂浆的损伤规律则恰好与之相反,路基上的CA 砂浆受压损伤最小,桥上最大。
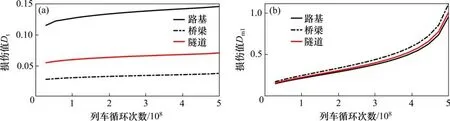
图6 列车循环作用下轨道板和CA砂浆损伤演化Fig. 6 Damage evolution of track slab and CA mortar under train cyclic effects
为了进一步反映轨道板和砂浆疲劳损伤演化对系统动力学响应的影响。图7给出了路基支承条件第1轮对下钢轨和轨道板垂向位移最大值。
从图7可知,随着轨道板和砂浆层疲劳损伤的形成与发展,钢轨和轨道板垂向位移均会出现不同程度的增大,轨道板位移、钢轨位移分别增大约77.50%和20.40%;此外,轨道板和砂浆疲劳损伤对系统动力响应的影响主要集中在损伤发展阶段的后期,特别是在砂浆层疲劳寿命仅剩10%~15%以后,系统动力响应将急剧增大。

图7 轨道板和砂浆层损伤演化下的系统响应Fig. 7 System response under damage evolution of track slab and mortar layer
4 结论
1) 不同的混凝土结构层疲劳损伤速率和最不利损伤位置、方向(纵向/横向)和方式(受拉/受压)均存在显著差别,应根据具体板型及轨道结构型式,开展疲劳损伤计算分析。
2) 所提出的车辆循环作用下无砟轨道混凝土结构疲劳损伤动力演化计算模型准确揭示了混凝土损伤的三阶段发展特性,良好把握了无砟轨道系统中混凝土结构的疲劳损伤动力演化规律。
3) 轨道板和砂浆层疲劳损伤对铁路工程结构系统的动力学响应影响主要反映在疲劳损伤的发展后期。
