对一道二元最值问题的解法探究

李一粲 吴云

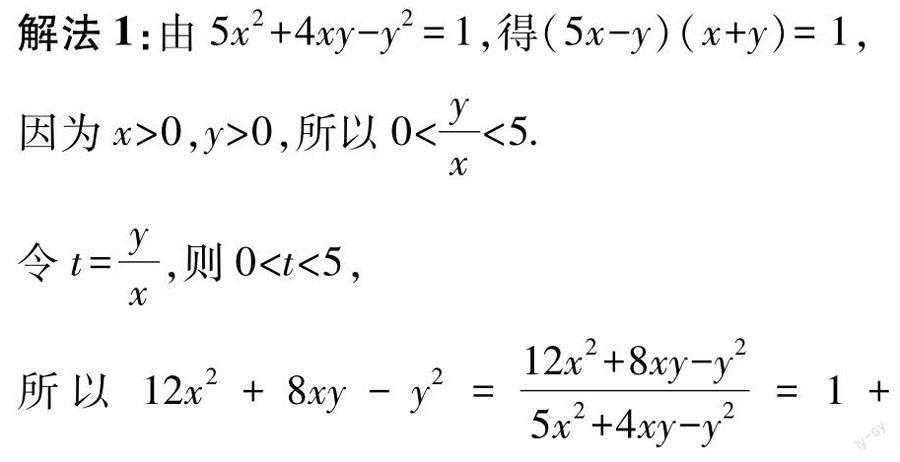
摘 要：最值问题是数学学习中普遍存在的一类典型问题，解法也是多种多样、优劣有别.遇到具体的最值问题，在尝试多种方法的同时，也需要根據具体情况选择合理、高效的解法.本文通过对一道二元最值问题的探究与分析，归纳这类问题的求解思路与策略，并对解法的适切性进行分析，以便更好地巩固所学的知识与方法，提高解题效率.

关键词：基本不等式；二元最值；一题多解

在高三数学复习中，二元函数的最值问题是一种常见的题型，它常常融合函数、不等式、解析几何等知识，具有综合性强、思维量大、技巧性强等特点，是数学学习中的一个热点及难点.在此知识点的学习过程中需要不断加强反思、归纳和总结解题策略，以此探究解题规律，揭示解题方法，形成解题技能.下面对一道二元最值问题的解法进行探究.

1 问题呈现

问题：已知正实数x，y满足5x²+4xy-y²＝1，则12x²+8xy-y²的最小值为                .

这是一个比较常见的二元条件极值问题，即在“正实数x，y满足5x²+4xy-y²＝1”的条件下，求一个类似式子12x²+8xy-y²的最小值.表面看起来两式形式接近，能比较容易找到两者的关系并恰当变换出目标，其实，真正处理起来还是有不少困难的，只有选择合适的路径方能有效解答.

2 解法探索

2.1 “1”的代换法

“1”的代换法是求最值问题时常用的方法，即用题目中或已知公式中与1有关的等式，将1用等式替换下来，变成较繁的式子，“欲擒故纵”，使后续的变换能够达到求出最值的目标.

2.2 双变量代换法

双变量代换法是通过设两个变量，换成另外一种对称的形式，进而转化成可以使用基本不等式等工具的形式，使问题得解.

评注：因式分解是双变量换元的基础和前提.途径2是先对求解目标恒等变形再求其最值，运算上优于途径1，解法2应该是该题的最佳解法.

2.3 判别式法

判别式法也是求解最值问题时常用的方法，即通过变换，将欲求的最值的式子转化成一个一元二次方程的系数，利用该一元二次方程有解时其判别式不小于零的特点求得最值.

解法3：

因为5x²+4xy-y²＝1①，

所以12x²+8xy-y²＝12x²+8xy-（5x²+4xy-1）=7x²+4xy+1，

评注：该解法首先利用①式将12x²+8xy-y²进行恒等变形，再将所求目标式子整体设参，从而表示y，再代入①中，通过换元得到③式，最后结合方程有正实数解进行求解.

2.4 基本不等式法

基本不等式法即为直接利用基本不等式成立的条件及相关性质，结合相应的变换而得到最值的方法.

此题还可以借助于“GGB”探究其几何背景.

方程5x²+4xy-y²＝1为双曲线的方程，令t＝12x²+8xy-y²，则t-2＝2x²+y²，t＞2，表示椭圆的方程.如图1所示，双曲线和椭圆的中心均为坐标原点，当t变化使得椭圆和双曲线相切时，t取得最小值，即为所求，这也是判别式方法的由来.该题的几何背景是研究两个二次曲线的位置关系问题，借助于“GGB”技术可以将抽象的数学问题具体化、可视化.它将“静态的”问题演绎成“发展的”“动态的”和“可视化的”过程，经历从抽象到具体的过程，实现从“不可见”到“可视化”的过程，更利于问题的发现、方法的形成、知识体系的构建、洞悉数学的本质，突破数学“难以意会，无法言传”的障碍，提升思维层次.

对于二元最值问题，首先还是要掌握基本的、常用的方法，比如通过代入、加减消元等手段将其一元化，转化为基本不等式或函数的求最值问题.其次根据题设条件挖掘一些隐含信息，了解试题的背景，不仅指导这道题怎么做，更要学会抓住问题的本质，归纳这一类问题的解题思想和方法，达到解一题通一类的效果.

参考文献：

［1］ 郭建华.“1”的美丽变身［J］.数理天地（高中版），2018（11）：13-14.