三阶幻方推导过程中的几个数学思想
2023-03-24秦奇侯欣于桓
秦奇 侯欣 于桓
摘 要:幻方是一个古老且具有魅力的数学问题,在当今数学乃至其它学科中具有广泛应用.本文旨在介绍一种适合小学生理解的三阶幻方的推导方法,并以此来体现几个数学思想在求解三阶幻方全部解的过程中的应用,强调数学学习以及数学教学过程中数学思想的重要性,以此倡导在数学教与学的过程中,多加体会数学思想在问题解决过程中的指导作用.
关键词:幻方;洛书;数学思想方法
1 问题介绍
幻方是古往今来数学研究中的一个重要问题.相传,大禹治水时途经洛水,有神龟出现,背负“洛书”,所示即三阶幻方的一个解.十三世纪,南宋数学家杨辉开展了对幻方的系统研究,后来欧洲一些国家也开始了这方面的工作.三阶幻方即如下问题:
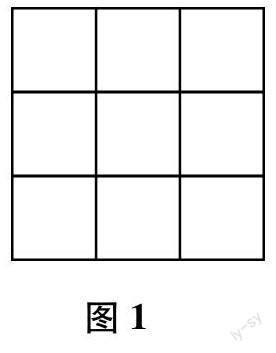
在图1的方框中不重复地填入1~9九个数字,使得每行、每列以及两条对角线上的数字之和相等.
三阶幻方对小学生来讲可以用试数的方法来求解,但这种方法花费时间长、效率低、学到的东西少.也有教师教小学生用罗伯法来解幻方,但只是背了口诀而已,并没有体现数学原理和数学思想方法,而且只能给出一个解,这种方法收获甚微.接下来将介绍一种适合小学高年级学生的三阶幻方求解方法,并详细分析求解过程中涉及的几个数学思想,以倡导学生学数学和教师教数学过程中应多体会数学思想的重要性,进而培养学生的数学素养,达到素质教育的目的.
2 三阶幻方全部解的求解过程
2.1 求解每行、每列以及每条对角线上的数字之和
首先,把第一行三个数字之和看成一个整体,用字母a来表示,那么第二行、第三行分别的三个数字之和也是a.注意到第一行、第二行、第三行所有数字之和等于1~9九个数字的和(这里运用到了加法交换律),即等于45,也恰好是三个a的和,那么可列出方程3a=45,从而求得a=15.又由每行、每列以及每条对角线上的数字之和相等,故每行、每列以及每条对角线上的数字之和均为15(相等的传递性).
2.2 求解中间方框的数值
现在已经知道每行、每列以及每条对角线上的数字之和均为15,这些和中与中间方框数值有关的和有四个:中间行、中间列、两条对角线,呈“米”字型.这四个包含中间方框数值的和的总和为15×4=60,其中,边上的八个方框中的数值加了一次,中间方框中的数值加了四次.而边上的八个方框中的数值加中间方框中的数值恰好是1~9九个数字各加了一次,等于45,再另外加三次中间方框的数值,就是“米”字型的四个和的总和.用字母b表示中间方框的数值,根据分析可列出方程60=45+3b,这样得出b=5.所以,中间方框的数值只能是5.
2.3 求解四个角上的数值
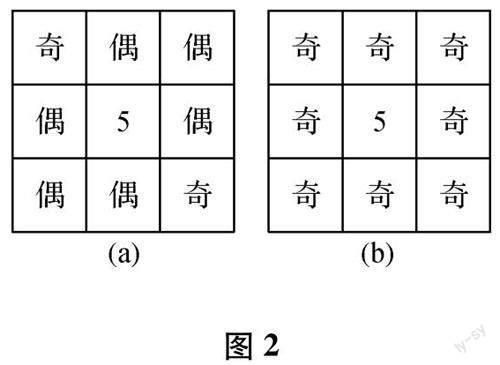
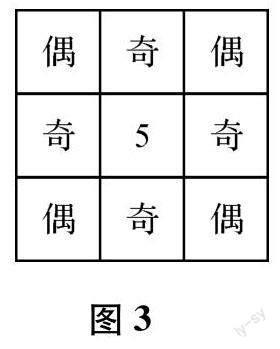
注意到四个角上的地位是“等价”的,可以任取其一进行取值情况的讨论,不妨先讨论左上角的方框,可取1~9中除了5之外的八个数值.咱们已经知道每行、每列以及两条对角线上的数字之和均为15,中间方框的数值为5,故同一条对角线上的两个角上的数值同奇同偶,中间行和中间列两头的数值也要同奇同偶.所以,可分奇偶简化讨论.若左上角的方框取奇数,则右下角也必定为奇数.此时若另外一条对角线两个角上的数值为偶数,由每条直线上的三数之和为奇数,可推出幻方中数值的奇偶性满足图2(a) 的情况,九个数中六个偶数三个奇数,与1~9中四个偶数五个奇数矛盾;若另外一条对角线两个角上的数值为奇数,可推出幻方中数值的奇偶性满足图2(b) 的情况,也与1~9中四个偶数五个奇数矛盾.故左上角取奇数时,无论哪种情况都不可能实现幻方.所以左上角必为偶数.由左上角是任取的四个地位“等价”的位置,故其它三个角上的数值也只能取偶数.
此时,幻方中数值奇偶性分布如图3,满足1~9中四个偶数五个奇数的事实.
于是,2、4、6、8四个数在四个角上,且由每条直线上的三数之和为15可得2和8在一条对角线,4和6在另一条对角线.那么,到底2、4、6、8哪个数填在左上角?实际上都可以,因为四个角的地位“等价”.不妨填2在左上角,则8在右下角,此时,未填的两个角的地位又是“等价”的.不妨填4在右上角,6在左下角.
2.4 填补四个边中间方框的数值
前面的步骤已经完成了中间和四个角上的方框的取值,使得每行、每列上的三个数中已经填好了两个数,再由每行、每列的和为15减掉已知两个数的和便可得到四个边上中间方框的数值,如图4.
2.5 全部解
前面第三步中最后在左上角的方框中填了2,但由于四个角的地位“等价”,这里填4、6、8也是可以的.故事实上左上角有四种填法.填完左上角后,同一直线上右下角的数值也就定了.这时,右上角和左下角的地位也是“等价”的,故右上角可填剩下的两个偶数中的任意一个,有两种填法.也就是说,左上角有四种填法,每种填法填好后,右下角的值就定了;右上角有两种填法,填好之后左下角的值就定了;再由第四步,三阶幻方所有值就定了.故共有4×2=8种填法.
3 三阶幻方求解过程中蕴含的数学思想方法
3.1 整体思想
求解过程第一步中,需要把每行的三个数字之和看成一个整体,记为a,并把1~9九个数字之和看成另外一个整体,等于45,从而得出每行的三个数字之和为15.这是利用了整体思想,不必第一步就要求出每個方框中的数字,利用整体思想,先求每行、每列、每条对角线的数字之和更有效.此方法可应用于很多小学数学问题,这里介绍一个代数例子.
明朝程大位所著《直指算法统宗》中有一个“百僧分馍”问题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”
利用整体思想可很快算出答案.假设一个大和尚与三个小和尚看成一个整体分一桌,共
4人吃4个馒头,这样一桌人吃4个馒头,那么100个馒头分25桌,每桌3个大和尚1个小和尚,最终算出答案大和尚人数为3×25=75,小和尚人数为1×25=25.
3.2 猜想验证思想
很多小学生可以猜得到中间方框的数值填5,因为9个数从小到大排列中间的数是5,但不确定填其它数是否可以.事实上,数学家在发现新的重要定理或结论的过程中总是先提出猜想,再想办法验证的.三阶幻方求解过程的第二步证明了中间方框的数值只能填5这一“猜想”.猜想验证是非常重要的一种数学思想方法,费马大定理、哥德巴赫猜想、四色猜想等数学史上著名的猜想引领着数学学者们前仆后继地研究,从而催动了数论、组合论等重要数学分支的发展及应用.有人曾猜想无论几次方程都有根式解,在后人验证的过程中证明出五次以上方程没有根式解.尽管最初的猜想是存在问题的,但收获更大,还开创了群论这一重要数学分支.在数学学科的学习中,学生应当多加思考,多去验证自己琢磨出的一些小“猜想”,教师也应引导学生发现规律并验证猜想.
3.3 方程思想
方程在数学课程与教学中占据重要地位,掌握方程思想能使学生更容易接收新的数学知识.在求解三阶幻方第一步中把每一行三个数字之和用字母a来表示,可列出方程3a=45,即1~9九个数字的总和.从而求得每行的三个数字之和为15,并且每列、每条对角线的三个数字之和也均为15.第二步中,把中间数值设为b,“米”字型的四个和的总和为60=45+3b,即可求出中间数.许多小学数学历史名题都有灵活多样、精彩纷呈的算术解法,锻炼了学生的思维能力,比如“盈亏问题”“鸡兔同笼问题”“牛吃草问题”……但它们无一例外也都有比较成熟的代数解法.培养学生用方程解决问题的意识,循序渐进地渗透方程思想,会让学生受益匪浅.
3.4 分类讨论思想
分类讨论是在求解问题或证明结论过程中,按照一定的标准,对所有情况分成几类,分别求解或证明的思想方法.分类时要注意所分类别要满足互斥、无漏、最简的原则.三阶幻方求解过程第三步中左上角的方框取值通过分奇偶两种情况讨论,从而避免了一个一个去尝试,加快了求解过程.左上角取奇数时,右下角也为奇数,进一步对另一条对角线上两个方框取值分奇偶讨论,从而最终得出矛盾,证明了左上角方框的取值必为偶数.分类讨论能够把问题化整为零,从而各个击破,得到最后的结果.常见的应用分类讨论思想来解决的问题如等比数列求和(分公比为1时和不为1讨论),再如过已知一点作与已知直线垂直的一条直线(分点在直线上,点在直线外讨论),又如求三阶幻方中有多少个正方形(分正方形含1个方框,4个方框,9个方框计数)等等.
3.5 假设思想
3.6 对称思想
三阶幻方求解过程中多次运用对称思想,第三步四个角的方框具有“等价”地位,只需讨论左上角的方框.因为其它方框可以由左上角方框通过旋转或对称得到.左上角取定之后,右下角也就取定了.这时再次利用地位“等价”,左下右上只需讨论其中一个的取值,另外一个可通过对称得到.这样,就注定了第五步求得的1个幻方,可通过旋转或对称得到另外7个幻方.事实上,这里的对称思想体现出了“二面体群”这一数学概念.幻方是一个正方形,正方形的二面体群是指正方形通过旋转、对称之后,与原正方形重合这样的变换的集合.其中包含旋转0度,90度,180度,270度四个旋转和以水平中心线、竖直中心线及两条对角线决定的四个对称.所以,正方形的二面体群中有8个元素,正好在此对应了8种幻方的填写方法.对称思想使得三阶幻方求解过程简化讨论,只得出一个幻方便可以推出其它幻方.值得一提的是,正是运用对称思想,五次以上一元方程没有求根公式这一结论才得以证明,也正是通过这一结论的证明,数学学者们才开始发展了群论这一专门研究对称性的数学分支.
4 结语
数学学科发展过程中数学思想起到至关重要的作用.在问题解决过程中需要用數学思想把问题化繁为简,这些思想的训练与培养需要落实到数学知识的学习过程中.最初数学概念的提出、猜想的验证、定理的证明等都离不开数学学者们对数学思想方法的理解与运用.教师在教学过程中应当总结并体会其中的数学思想方法,再以此为指导设计课程,让学生在学的过程中充分体会数学思想的价值所在,进而使学生在未来的学习及解决问题过程中深度思考,利用数学思想方法将问题化繁为简,这也是数学核心素养的体现.类似于幻方这样的具有探究性的数学问题有很多,比如鸡兔同笼、孙子定理等.教师应当多加思考总结,深度挖掘这些数学问题解决中每一步用到的数学思想,并渗透到教学中,使得学生数学思维得到锻炼,数学核心素养得到提高,这是教学过程中更应注重的地方.
参考文献:
[1] 高汉城.由河图洛书产生的对传统数学及当下数学教育的思考[J].数学之友,2022,36(10):2-4+11.
[2] 唐兆能.怎样快速编制幻方[J].中小学数学(小学版),2023(Z1):122-123.
基金项目:北京联合大学教改项目:学生为中心小班制互动式教学模式改革研究——以教育研习为例(项目编号:JJ2023Q002);
中国高等教育学会2023年度高等教育科学研究规划课题重点项目:基于教育数学思想的师范生《线性代数》教学研究与实践(课题编号:23SX0302).
