利在构造 功在思维

于健　郭建华

摘 要：数学教学一个重要任务是让学生学会思考、锻炼学生的思维能力.对于解题教学，要培养学生分析问题、发现问题的能力，培养学生思维的深刻性.文章通过对构造二阶递推数列模型解决3类概率问题的探究分析，向读者阐述了此类问题的命题方向、特点以及运用思维导图等解题策略，发展学生思维能力.

关键词：二阶递推数列;概率;思维导图;思维能力

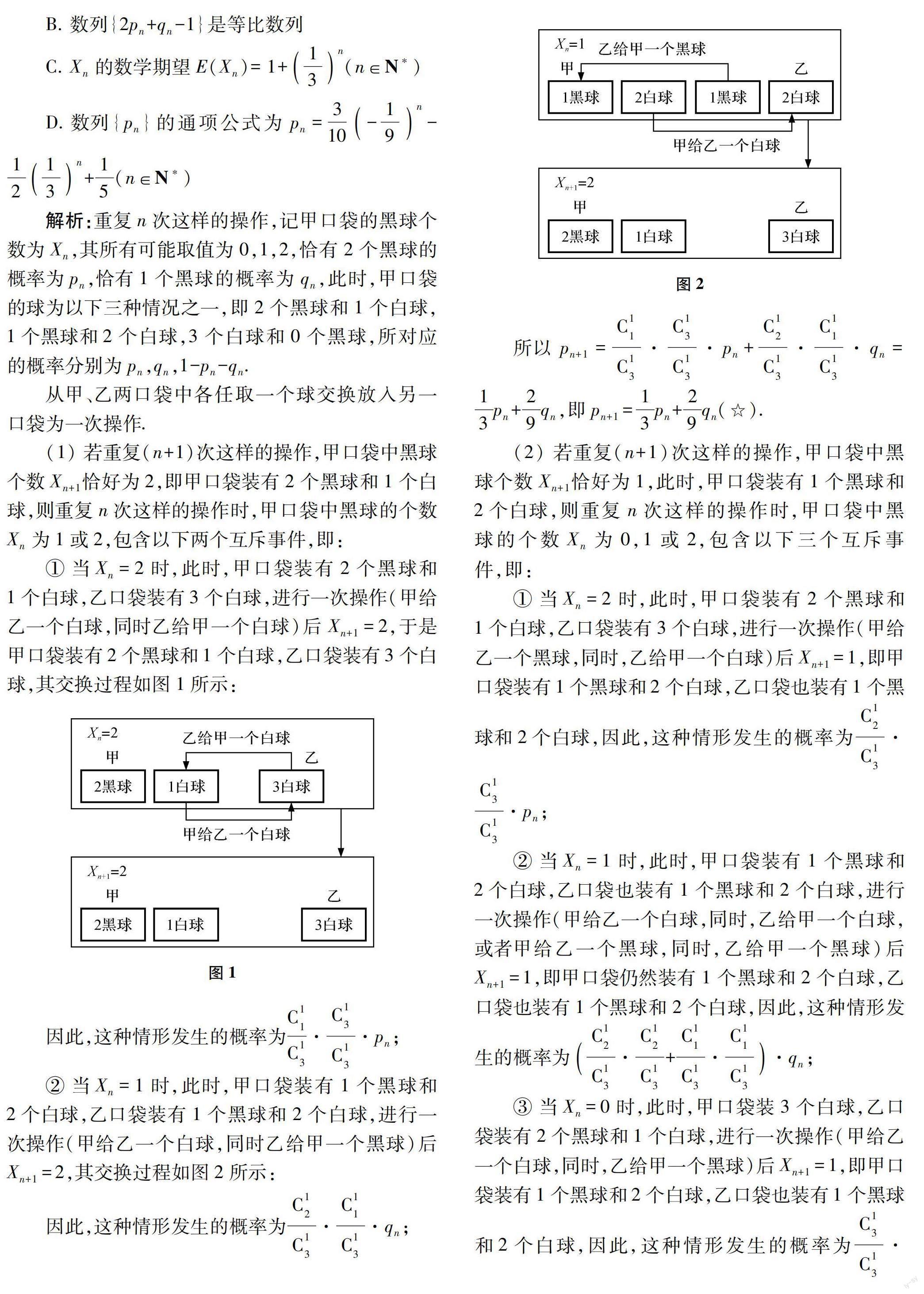
评注：用递推数列解答概率统计题是大学自主招生和竞赛命题的热点，也是学生学习的难点.该题是一道典型的投骰问题，分析方法同例1，依据思维导图，厘清第（n+1）次由A掷的条件是求解P_n+1与P_n的关系及P_n通项的关键，再结合从特殊到一般的方法求解.

通过以上案例分析，探索P_n与P_n+1的遞推关系是求解这类问题的关键，其解题步骤为：首先理解题意，弄清楚相邻事件间发生的关联，利用分类讨论思想或以思维导图探寻两项或三项的递推关系；其次，利用条件概率和互斥事件等概念，正确建立递推关系；最后，利用数列的相关知识对递推关系进行求解.

4 结语

构造a_n+1＝qa_n+p（其中p，q为常数，pq≠0，q≠1）的数列模型求解概率问题，此类问题情境丰富，综合性强，求解难度大.侧重考查数学建模能力以及创新能力、转化与化归和分类讨论等数学思想，问题常把不同学科之间和同学科不同知识模块之间的知识进行融合，这也是新高考试题的亮点和热点.它也是落实“四基”，培养“四能”的重要考查形式，为数学核心素养的考查提供重要的载体.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准［M］.北京：人民教育出版社，2019.