构建学习共同体 提升数学学习品质

林曦

“学习”日益成为教育研究的重要领域，教师不能只局限于“教”，不能眼里只有教材和教法，更要看得见“人”，将重心落于如何指导、帮助学生更好地“学”。构建学习共同体，给予学生课堂主体地位，让学生有公平、润泽的学习环境，使其在自主学习和合作交流中展开真实、有品质的学习。数学是一门逻辑性、抽象性较强的学科，只有让数学基础各异的学生学有所思、学有所获，体会到学习的乐趣、数学的智趣，才可以为可持续学习打下坚实的基础。

一、构建学习共同体，创设公平的学习机会

学生经历六年的小学学习进入初中阶段，因为思维能力、学习习惯的不同以及各种非智力因素的影响已经形成不同的数学基础，而初中阶段课业要求加大、节奏加快，使得不同层次的学生均面临新的学习挑战。对教师而言，传统秧田模式的讲授课堂和多年课改引进尝试的小组合作学习，哪个才是公平、高效的？如何才能真正让学生更好地学习，收获知识的增长和素养的提升？佐藤学提出：真正好的教育是“公平”与“质量”的兼顾，教师的责任“不是教一节好课，而是保障所有学生的学习权”。秧田模式的讲授课堂多数只见教师不见学生，或者课堂只属于可以呼应教师的部分学生。小组合作学习又往往停留在简单地分小组，进行表面化的合作学习，更多时候为公开教学的表演而生。而学习共同体是要形成课堂内外长效的学习状态，让每個学生在学习共同体中都能感受到被看见、受重视。基础偏弱的学生觉得课堂也有他们的一席之地，而不是被动地被课堂抛弃；思维灵活的学生感觉学习可控而又有挑战，不同层次的学生都能感受到公平、安全、滋润，从而生发出更多的主动性，真实学习而又互相促进。佐藤学将“民主性”“公共性”和“卓越性”作为学习共同体的三大教育哲学，教师构建学习共同体亦要将这个教育哲学付诸实践。

构建学习共同体的第一步是分组。有的教师会单一以学生在教室的空间位置，如前后桌、同行同列等形式划分，虽然便于课堂交流，但忽视了其他影响因素。构建学习共同体应结合学生的兴趣爱好、性格特征以及成绩等多维度进行分组，还应结合每个共同体小组的发展目标来构建。在实践过程中，不同的班级生情应有不同的策略，在学生程度差异较大的班级甚至可构建多模式的共同体。比如，基础较好、思维活跃的学生可以招募式自由组合形成3～5人小组，这类共同体可在课堂之外自发地对拓展问题展开钻研探讨，甚至开展一些专题性的研究，成员间的思维碰撞有利于激发更多的学习兴趣，提高思维层次。而其他大部分的学生由教师综合考量后组建共同体，也可征询学生意见进行个别调整。这种模式的共同体是课堂教学活动关注的主体，教师的教学设计应适合他们的思维能力，充分调动他们的积极性，让他们在共同体中能开展自我学习，同时获得帮助和滋养。

二、推进学习共同体，保障真实的学习过程

学习共同体设立后，教与学都应有所调整，以便推进学习共同体的开展，保障真实的学习过程，而不是把共同体作为一种表面存在的形式。以“完全平方公式”教学为例，谈谈课堂设计与教学如何推进学习共同体的开展。

“完全平方公式”在人教版教材中的设计是通过一组特例的计算、比较、分析、归纳，抽象出一般结论，进而通过符号推理获得公式的符号表示及语言表述，体现从特殊到一般的思想方法。故从“完全平方公式”的代数运算功效上考虑，笔者在“综合共同体”中设计了从数字的计算—猜想—简单验证—部分抽象验证—证明，这样的探究过程（方案1），以期遵循探究数学原理的一般程序：观察—归纳猜想—验证—证明，这是初中阶段大部分的原理教学采用的探究路径，特别在几何的一些定理中，如内角和公式、勾股定理等。数学思维中，归纳推理在于发现结论，归纳能力是创新能力的重要基础。数学教学过去强调“双基”，缺少对学生归纳能力的培养，而概念、定理、公式、法则等原理教学的核心就是“归纳”。方案1的设计，旨在让学生真正经历“由特殊到一般”公式的发现和归纳过程。

问题：1012=（100+1）2=？

计算猜想：1012=（100+1）2=（100+1）（100+1）=

=

口算验证：112=

212=

计算验证：（a+1）2=

一般地：（a+b）2=

从单元整体考虑，在学习本节课之前，学生刚刚学习了“平方差公式”，类似方案1的设计用“平方差公式”来探究比较合适，而在乘法公式的第二节课“完全平方公式”中，教师可以引导“自由共同体”的学生思考知识的生发点。“平方差公式”和“完全平方公式”都是多项式乘法（a+b）（p+q）的特例，因此在方案2中抓住多项式乘法这个知识生发点，引导学生在多项式乘法的基础上探究特例，切合知识的发生发展过程和内在的逻辑线索，符合学生的认知规律，并且应用与“平方差公式”类比的方法，从符号、文字、图形角度全面认识“完全平方公式”。这样的过程，让学生在参与中更加自然地收获了公式原理。

方案2：

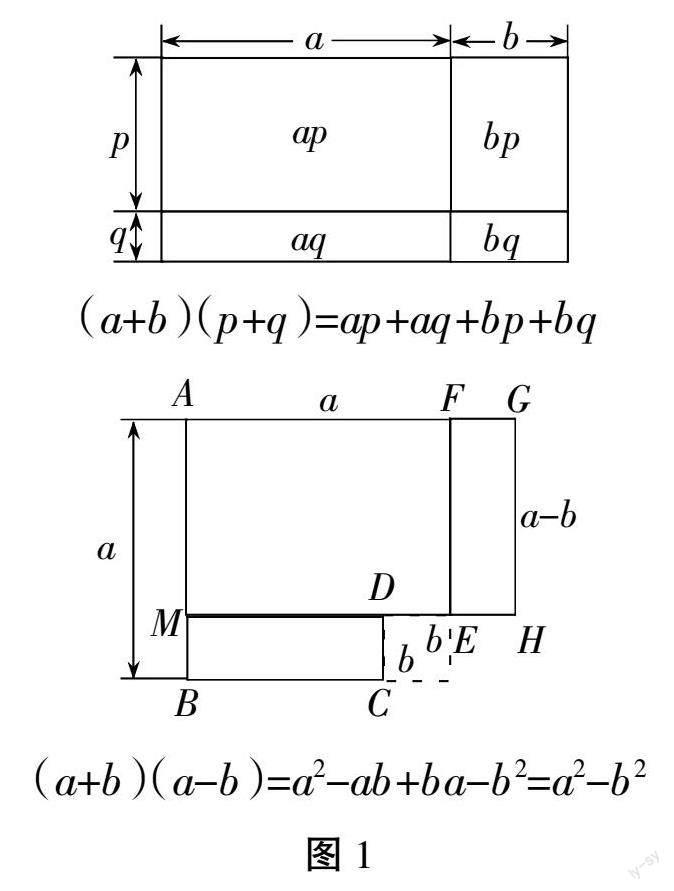
（a+b）（p+q）=ap+aq+bp+bq

（1）当p=a，q=-b时，（a+b）（p+q）=（a+b）（a-b）=a2-ab+ba-b2=a2-b2

（2）当p=a，q=b时，（a+b）（p+q）=（a+b）（a+b）

即（a+b）2=

语言表述：两个数的和的平方，等于    。

（a+b）（p+q）=ap+aq+bp+bq

（a+b）（a-b）=a2-ab+ba-b2=a2-b2

思考：你能类比以上图形，画图说明“完全平方公式”吗？（请先独立思考，尝试画图，再互相讨论。）

原理教学中若能让学生去追寻、探索知识的生发和相关知识的结构关系，就能使学生更加自然地学习相关的知识、原理，同时在“自然而然”中享受“水到渠成”的成就，感受知识生发的魅力。初中数学中“无理数”“直角坐标系”等内容都是人类数学探索历程中闪亮的火花，教师在指导学生学习时若能让其体验它们的生发，在“生发”中掌握相关的知识，同时感受知识流淌、思维前进的美好，这对提升学生学习数学的兴趣、增强学好数学的信心无疑有巨大的作用。因此，教师可借助学习共同体，力求让不同思维和能力的学生都能学好原理，课堂教学的设计要符合不同学生的认知规律，关注学生的“四基”发展，引领学生深度学习，使学生从“学会”到“会学”，优化思维品质，提升学生的数学核心素养和综合素质。

初中数学有着诸多的公式、定理、规律，要想让学生在学习过程中获得知识，并了解知识的产生、发展过程，理解探索知识的研究方法，就要引导学生善于发现问题，学会用数学的眼光看待問题。这节“完全平方公式”知识、技能的掌握是显性的，是学习的“明线”；而思维的发展是隐性的，是教学中的“暗线”。数学课堂既要“授之以鱼”，又要“授之以渔”，离开知识、技能的掌握来说思维的发展是“空中楼阁”，而只有知识、技能的掌握却不关注思维发展的教学是“鼠目寸光”。知识、技能与思维发展相辅相成、相得益彰。这节课中贯穿着一般到特殊、特殊到一般，既有归纳的合情推理，又有应用的逻辑推理，既有数与形的转化，又有差与和的转化，这些都能促进学生的思维发展、学习能力的提升，于学生可终身受益且可持续发展，这样的教学才是有生命力的，学生在共同体中“双线”的牵引下的学习才是深入有效的。

当然，不同的共同体采用不同的导学方式，对课堂时间的分配，课堂中各共同体的引导、调动上都是个考验。日常的教学要根据教材和生情采用分中有合、合中有分的方式推进共同体的每一节课的学习活动，这样绝大部分的学生可以在自己的共同体中开展真实有效的学习。教学只有适合共同体特质的节奏、梯度、难度才能兼顾“公平”和“质量”。

三、巩固学习共同体，提升科学的学习品质

共同体的学习包含三个层次的目标：就学生个体而言，学生要能够安心而真实地学习；就学生群体而言，学生之间相互平等，彼此倾听，互相学习，从而让课堂成为“交响乐”；就品质而言，学生的学习应该有更高的品质，学生可以通过完成高挑战、高质量的学习任务得到全方位的发展，最终成为一个自主的学习者乃至深度学习者和创造者。因此，共同体的学习活动不局限于课堂，课后的学习也可以继续巩固、延伸学习共同体的作用。

对于“自由共同体”中的学生，“完全平方公式”这节课中无论是知识的发展还是学习思考的深入都有值得再进一步的价值，而此时若能挖掘好这个价值，无疑对这类学生数学素养的提升有很大的帮助。因此，笔者设计了如下环节。

（a+b）（p+q）=ap+aq+bp+bq

当p=a，q=b时，（a+b）2=a2+2ab+b2

“完全平方公式”是多项式相乘的特殊形式，探究将“完全平方公式”特殊化或一般化能得出什么有价值的公式？

（1）两数和的平方若改成三数和的平方、n数和的平方，如何解决？你能发现什么规律？

（2）两数和的平方若改成两数和的立方、两数和的n次方，如何解决？你能发现什么规律？

当然，这个环节在课堂中因时间原因只能抛砖引玉，教师可以引导学生在课后通过研究性学习活动，形成小组的研究报告。这样既拓展了课堂的时间，又让学生对“完全平方公式”有了更完整的认识，既明确它的“源”（多项式乘法），又清晰它的“比”（平方差公式，自身还有和与差两种形式），还看见它的“展”（n项和的完全平方、两项和的n次方）。

学生真正经历这样的探究，就好像参与到“完全平方公式”的“前世”“今生”和“未来”，充分感受知识生成、发展的魅力，同时学生的符号意识和几何直观等数学素养也能得到提升，在感受归纳和演绎的过程中逻辑推理能力和有条理的表达能力得以提升，科学精神和探究品质、创新能力得以升华。数学课堂离不开数学的本源，但数学课堂又不能仅止于数学。教师在整个课堂内外的学习共同体中，也能感受到学生的思考过程，思维的成长变化，进展与卡壳的节点，欣喜和沮丧的真实，于教师也是一个不可复制的过程，是一个与学生发展共育的生命旅程。同样，对于“综合共同体”中的学生，通过多种形式的课内自我评价、相互评价及课后互助等多渠道激发学生的自我学习和共同学习，以达到提升学习效率和品质的目标。

《义务教育数学课程标准（2022年版）》强调“要让学生会用数学的眼光观察世界、会用数学的思维思考世界、会用数学的语言表达世界”，通过构建学习共同体，指导不同水平的学生在“生发”处学习认识数学，学生在思考探索的“深化”中把握数学的逻辑，领悟数学思想方法，感悟其间所蕴含的科学方法、理性思维，并在师生的共同学习探索过程中达成素养的“升华”，养成良好的学习习惯，最大限度地收获学习的价值。

（作者单位：福建省福州第八中学）

编辑：赵文静