单元整体化视角下小学数学结构化教学

杨明敏

单元整体教学是在单篇课程学习的基础上，通过整合一个单元内的课程知识，经过综合梳理、排列，而重新定义、设计的一种教学模式。结合单元整体教学可以补充单篇课程中存在的缺乏知识间联系、学习效率低等问题。本文以人教版数学四年级下册“三角形”教学为例，探究如何在单元教学中实施结构化教学，以此提升学生在数学学习中的迁移、应用能力。

一、小学数学结构化教学的要点

小学数学结构化教学是指通过促进新旧知识、新旧经验的相互作用，构建具有普遍联系、开放、生长的知识结构和经验结构的过程。在此过程中，教师需要挖掘新旧知识之间的联系，构建知识框架，并在此基础上，提炼学习方法，提升学生的学习效率。

（一）整合新旧知识，提升学习效率

旧知识是指学生此前已经掌握的数学基础知识，新知识是指学生即将学习以及未学习的内容，结合本文而言，新知识是指人教版数学四年级下册“三角形”教学的内容，包含：三角形的分类、性质、面积计算方法等。基于数学结构化教学，教师需要从旧知识上挖掘与新知识的联系点，如利用已知的图形性质来引入“三角形的特性”的概念，由此提升新知识的理解和记忆。结合单元教学而言，在整个单元教学设计过程中，教师围绕本单元的教学顺序，要有意识地构建从已知到未知的桥梁，由旧知识引到新知识上，由此激发学生的学习动力和探索欲望。

（二）构建知识框架，把握核心要点

“结构化教学”本质上是一种深入挖掘和强调数学知识内在联系的教学方法。这种方法不仅关注单一的数学概念或技巧，更重视探索不同知识点之间的共性和差异性。通过对比分析，教师可以和学生共同寻找各个概念之间的联系和差异，从而构建全面且有深度的知識框架。在单元教学中，构建知识框架的过程涉及将教学内容组成一个有序和连贯的结构，这就要求教师不仅要传授单个数学概念，还要展示这些概念是如何相互联系和作用的。例如，在“三角形”授课时，教师可以将三角形的属性与之前学习的其他几何形状的属性进行对比，帮助学生理解三角形在几何学中的独特地位和作用。

（三）注重迁移应用，掌握学习技巧

结构化学习的目的是在学习了本阶段的知识之后，能够有能力去解决问题，强调实践、迁移学习的能力，而非单纯地知识授课。因此，在教学过程中，教师不仅要注重知识的传授，还要重视知识的应用和迁移。具体而言，在教学过程中，教师不仅要让学生学会数学公式和定理，还要培养他们将所学知识应用到新情境中的能力。在单元教学背景下，教师要合理地评价学生的学习过程，不仅要评价学生的学习结果，还要评价学生在整个过程中思考问题的方式、方法，由此来判断学生是否掌握了本单元学习的关键性技巧。

二、单元整体化视角下小学数学结构化教学

上文重点探究了小学数学结构化教学开展的要点以及在单元教学中，该如何实施结构化教学。据此，以人教版数学四年级下册“三角形”为例，探究如何在大单元教学的背景下，构建结构化教学框架，以此探究如何在小学数学单元教学中实施结构化教学。

（一）研读教材内容，构建知识联系

《义务教育数学课程标准（2022年版）》（以下简称《新课标》）提出，教学目标的确定要充分考虑核心素养在数学教学中的达成。每个特定的学习内容都具有培养相关核心素养的作用，要注重建立具体内容与核心素养的关联，在制定教学目标时将核心素养的主要表现体现在教学要求中。据此，基于单元整体教学下开展结构化教学，教师首先要深入研读教材内容，包括对每个知识点的详细理解，还涉及探索这些知识点之间的联系，由此探索如何从“小目标”“小知识点”中，构建“大单元”与“核心素养”。在确定了这些关键的教学点后，教师可以根据学生的学习能力和需求构建不同的难度阶梯，梳理知识内容，从而构建知识点之间的联系。

例如，人教版数学四年级下册“三角形”单元教学中，首先，教师分析学生的学情可以看出，四年级的学生虽以具象思维为主，但已经开始向抽象思维过渡，不过整体的分析、综合、归纳、概括能力还比较薄弱。因此，在教学过程中，教师要采取适合学生认知水平的教学策略，逐步引导学生从具体的实例出发，理解和掌握三角形的基本概念和性质。其次，教师可以设计一系列的活动，如小组合作、问题探究等，来激发学生的兴趣和参与度，使学生在实践中加深理解。最后，针对学生分析、综合、归纳、概括能力较弱的情况，教师可以设计一些引导性的问题和讨论话题，通过讨论和互动，帮助学生逐步提高这些能力。教师还应注重培养学生的观察能力和思维能力，通过观察、比较、分类等活动，使学生更深入地理解三角形的特点和规律。

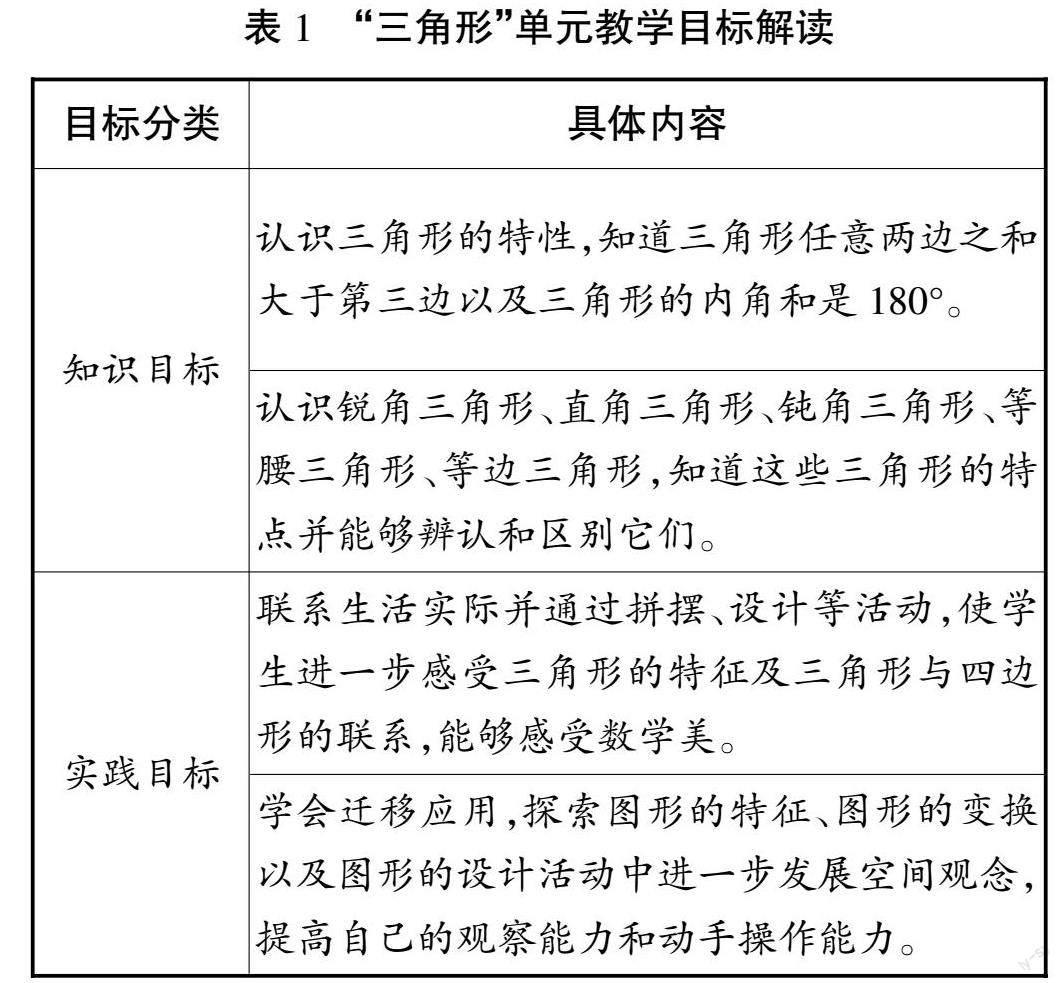
结合教材内容分析，本单元的教学目标如表1：

围绕本单元的知识目标以及实践能力目标，教师可以将本单元的知识点进行细化，具体包含：“三角形特性的了解”“三角形分类的认识”“三角形的内角”“运用三角形的内角和求多边形的内角和”四部分内容。难度等级可以从“三角形特性的了解”出发，教师在引导学生了解三角形的边、角特点之后，延伸拓展新知识“三角形分类的认识”，并了解三角形“特征角”角度之后，引导学生了解“三角形的内角”，并尝试“运用三角形的内角和求多边形的内角和”。由此，形成四级难度阶梯，帮助学生构建更牢固、广泛的几何知识框架。

（二）探寻认知起点，构建知识框架

为保障单元教学的内容更加贴合学生的需求以及要求，了解学生当前的知识水平和理解能力是至关重要的。在教学过程中，教师可以通过预测试、问卷调查或课堂讨论以评估学生对之前学习内容的掌握程度，以及他们对新单元主题的初步理解。基于这些信息，教师可以确定学生的认知起点，这是构建知识框架的基础。

在人教版数学四年级下册“三角形”单元教学过程中，教师有必要探索学生的认知起点，即通过“前测”的方式（如表2），了解学生1～3年级几何学习的情况。

此后，教师需要结合“前测”结果，设计一个全面且灵活的教学计划，其中明确指出单元的主要概念、技能目标以及预期成果。例如，在以上“前测”中，教师发现学生对于三角形三对边之间的关系认知不清，基于整个单元教学，就要利用“三角形的特性”“三角形的分类”“三角形的内角”这三节与此相关的课程，着重渗透，由此提升学生对此类知识的掌握情况。

此外，构建本单元知识框架时，教师还应强调知识间的联系和逻辑流程。通过将新概念与先前学习的知识相连接，教师可以帮助学生构建一个连贯的知识体系。例如，“三角形”这一单元隶属于“图形几何”知识内容，在1～3年级学生涉及“平面图形”“角的初步认识”“长方形和正方形”“平行四边形和梯形”四部分知识，在本单元教学过程中，教师可以从以上知识出发，尝试与三角形相联系，从而将新旧知识衔接。如在“三角形内角和”关系学习过程中，教师可以结合此前“角的初步认识”引导学生去测量三角形内角的角度；在“运用三角形的内角和求多边形的内角和”这部分学习中，教师可以结合从“拆解正方形”出发，尝试通过“拆解”的方式，引导学生探究正方形的内角和，以此进行迁移求出多边形内角和。

教师可以通过“前测”来了解学生对三角形基础知识的掌握情况，可以有针对性地规划教学内容，确保教学活动既能衔接学生现有知识，又能引导他们掌握新概念。此外，在构建知识框架的过程中，强调知识间的联系和逻辑流程，不仅能帮助学生将新的数学概念与以前学过的知识相结合，还能促进他们的批判性思维和创新能力。通过这种教学方法，教师不仅可以确保学生在单元教学过程中的学习效率，还可以激发他们的学习兴趣，促进他们综合思维能力的提升。这样的结构化教学方法无疑是提高教学质量和学生学习成效的重要途径。

（三）梳理核心知识，学会迁移应用

结构化教学的目标是通过知识的迁移学会知识的应用。《新课标》中对小学阶段“图形与几何”部分提出了新的要求，要求教师要强化学生对图形的认识和测量的整合，凸显两个主题之间的内在联系，注重从整体上理解和掌握这些内容，并使学生形成知识与方法的迁移。这与结构化教学中注重知识的迁移和应用不谋而合。据此，在教学过程中，教师要学会引导学生从课程出发，提炼出单元核心的知识点，并尝试在其他类似的题目、课程学习过程中能够高效实用，由此实现新课程标准中培养学生用数学思维思考问题的能力。

例如，在人教版数学四年级下册“三角形”单元教学过程中，教师可以结合本单元的内容构建项目学习活动，通过结合“三角立体房子”的设计，让学生亲自动手，利用一张“正方形纸”构建一个立体的房屋角落。在这个过程中，学生需要思考如何将纸切割和折疊成三角形的结构，同时考虑三角形的稳定性和美观性。这不仅需要学生应用三角形的基础知识，还要求他们运用几何学中的空间感知和构造技巧。在这种项目中，教师鼓励学生运用创造性思维，将课堂上学习的理论知识转化为实际操作。通过将数学知识与现实世界的物理对象相结合，可以使学生更直观地理解三角形的属性和应用，也能使学生体验到数学知识在现实世界中的实际应用价值。

教师在教学过程中引导学生从课程出发，梳理核心知识，并学会在实际操作中迁移和应用这些知识，从而有效地培养学生的数学思维能力。这种结构化教学方法不仅提高了学生的学习兴趣和参与度，还有助于他们在解决实际问题时灵活运用数学知识。

结构化教学不仅关注知识的传授，还强调知识的深度理解和广泛应用。通过构建知识框架，教师能够更好地连接新旧知识，帮助学生构建连贯的数学知识体系。同时，通过梳理核心知识，学生可以学会将这些知识迁移到不同的情境中，从而提升数学思维能力和解决问题的能力。基于数学课程特点及学生实际情况，本文从课程内容整合、优化课堂结构及发展学生思维等方面实施结构化教学，可以使学生的数学学习呈现出整体性、系统化、结构化的特点，真正发展学生的数学思维，促进学生数学核心素养的形成与发展，为学生今后的学习奠定基础。

（作者单位：平凉市崆峒区峡门回族乡峡门小学）

编辑：赵文静