大概念 大单元 大数学

雷丽珍

一、整合单元内容，提取大概念

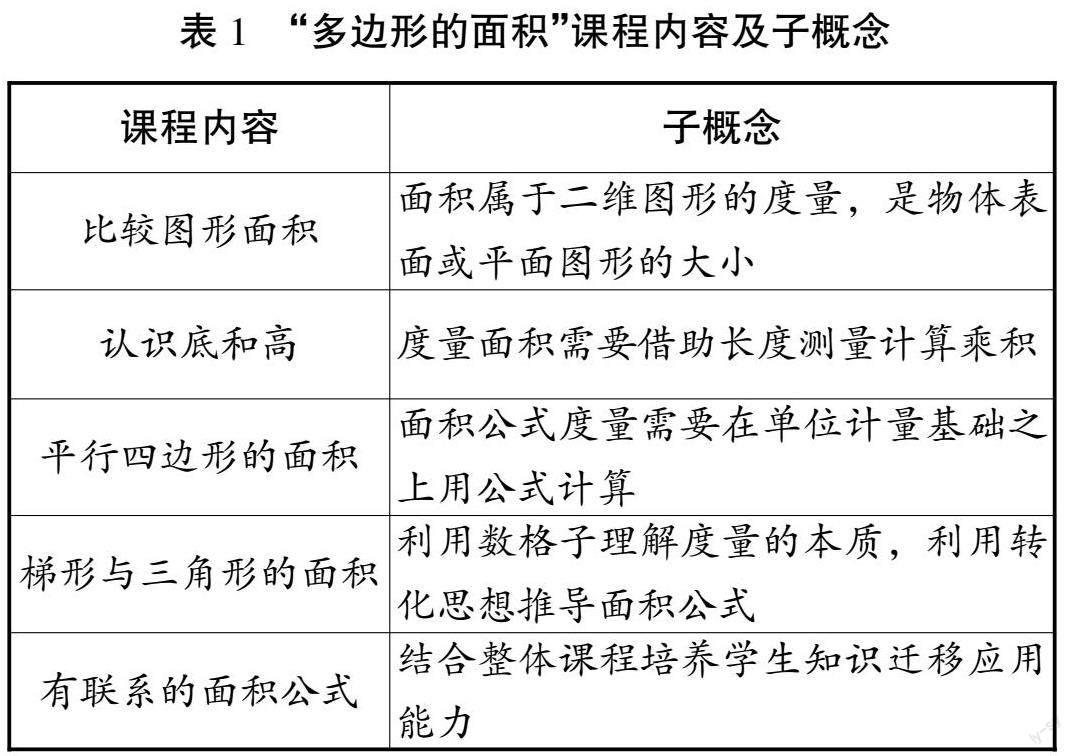
通过梳理《义务教育数学课程标准（2022年版）》（以下简称《新课标》）中有关“多边形的面积”的教学要求与人教版小学数学五年级上册第六单元“多边形的面积”的内容，笔者将该单元内容重组，将教学内容确定为五个板块（见表1）。依据《新课标》，该单元的“大概念”可确定如下：

1.渗透“转化思想”，将“未知”转化为“已知”，用所学的方法解决新问题。

2.发展量感、数感、抽象素养和推理素养。

基于“大概念”，五大板块课程内容所对应的子概念体系有所不同。（如表1所示）

二、外显大概念，制订大目标

1.知道平行四边形、三角形、梯形之间的联系及对应图形的面积计算公式。

2.通过动手操作、观察分析、数学计算经历面积公式推导过程，感受数学转化思想、建模思想。

3.用数学符号感受现实世界中的数学关系，感受数学在生活中的价值。

三、活化大概念，生成核心问题

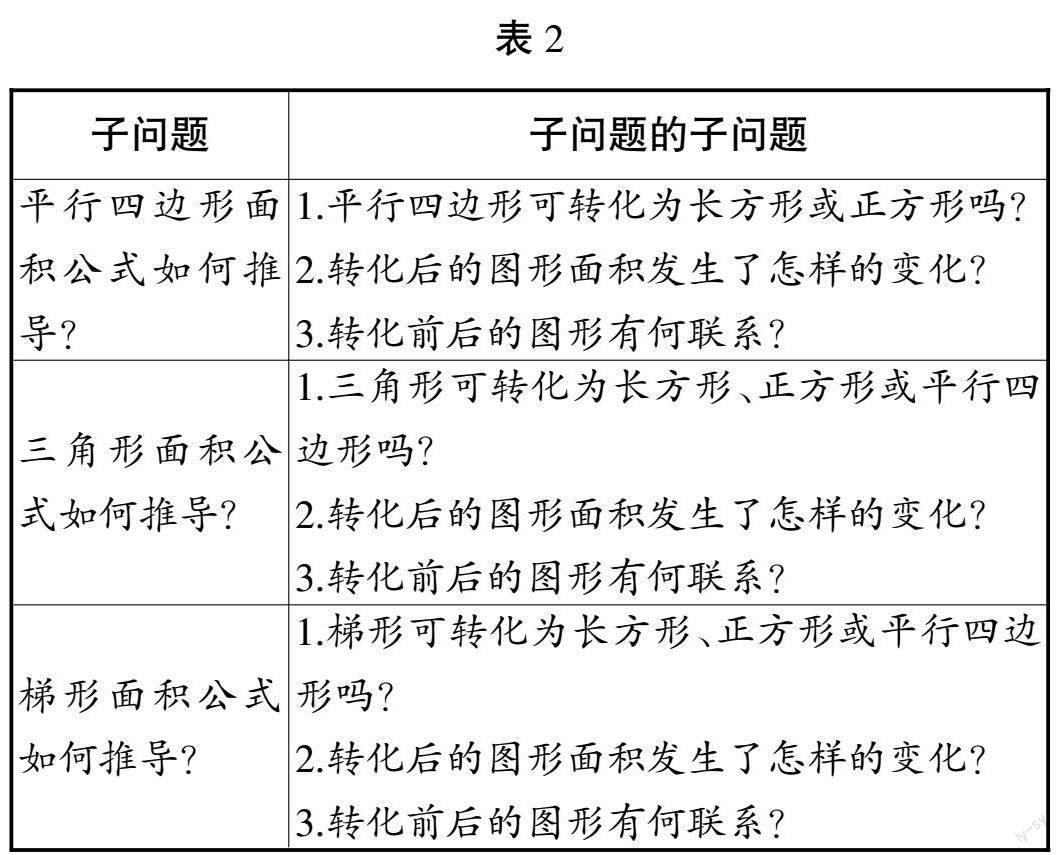
基于“大概念”的小学数学大单元教学过程中，教师需要立足“大概念”的特征生成核心问题。在“多边形的面积”大单元教学过程中，教师可围绕数学“转化思想”这一大概念提出“多边形的面积公式之间有着怎样的联系？”这一核心问题，并以此核心问题细化子问题、子问题的子问题（如表2所示）。

四、构建大概念，开发学习活动

（一）子课时学习活动设计

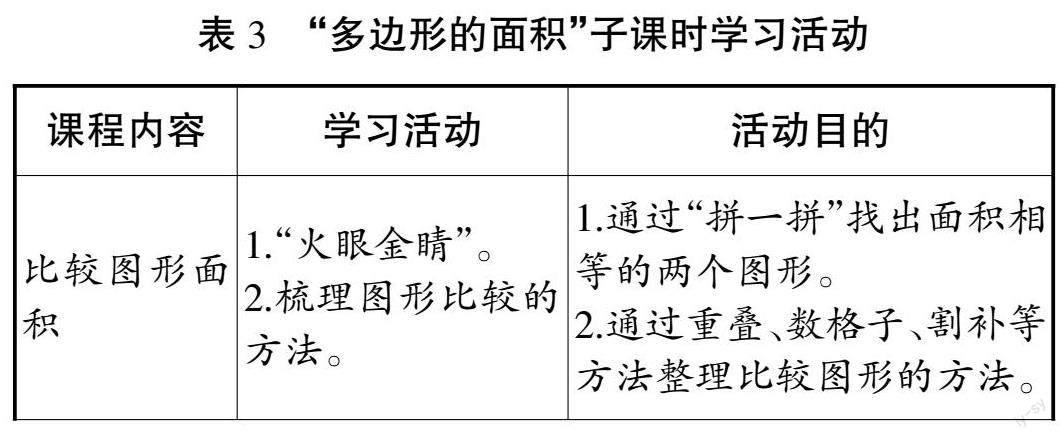
立足“大概念”，本单元教学活动设计主要围绕“转化思想”和“多边形面积”开展，不同课时对应的学习活动有所不同。（如表3所示）

（二）子课时学习活动实施

为了直观呈现小学数学大概念、大单元教学操作步骤，笔者节选“多边形的面积”大单元教学中“比较图形面积”“平行四边形面积”部分教学活动做出示范。

［案例一］比较图形面积

1.情境创设，勾起回忆

师：同学们，我们在1～4年级已经接触了很多平面图形了，你们还记得有哪些吗？

生：长方形、正方形、三角形……

师：教室里面有哪些你熟知的平面图形呢？

生A：桌板、窗户，这些是长方形的。

生B：红领巾是三角形的。

师：之前我们大家已经接触过长方形、正方形的面积公式，大家能够计算出桌板、文具盒表面的面积吗？

学生计算。

师：那咱们红领巾的面积是多少呢？大家能够思考出红领巾的面积与我们桌板、文具盒面积的关系吗？

（设计意图：此环节通过问题引导带领学生复习长方形、正方形的面积公式，激活学生的已有经验，为新知学习打下基础。同时利用“红领巾面积与桌板面积、文具盒面积关系”这一问题，激发学生的探究意识，引出本课教学主题“比较图形面积”。）

2.感知转化，积累经验

多媒体课件出示图1。

师：请同学们观察课件中的图形，你们能够比较出它们的面积关系吗？你有怎样的发现？将你的发现与组员进行讨论。

A组：我们组发现①和③面积大小相等，因为它们两个的边拼起来是一个正方形。

师：拼接成正方形就意味着面积相等了吗？有没有其他小组有异议的？

B组：①和③是可以完全重叠的，所以面积相等。

师：那请问A组的论述如何证明？

B组：因为①和③对角线是分开的，之前我们学过轴对称图形，因为对角线分开，所以面积相等。

师：是的！我们用重叠法找到了①和③面积相等，那还有其他小组可以证明这两个图形面积相等吗？

C组：还可以数格子！①和③拼成一个正方形共占了9个格子，两个三角形被平均分成两份，每一份占4.5个格子，两个图形占据格子数量相同，所以面积相同。

师：是的，这是我们常见的“数格子”方法。还有其他小组可以利用刚刚讲到的方法寻找其他平面图形的关系吗？

A组：⑧=⑨=⑩、②=⑤=⑥。

师：还有其他发现吗，同学们？

D组：①+③=⑦，①和③拼接起来刚好组成一个边长为3个格子的正方形，⑦是平行四边形，可以通过割补法将⑦变为边长为3个格子的正方形，所以①+③=⑦。

师：总结得不错！大家能够利用割补法寻找其他图形的关系吗？

生：②+⑥=⑧=⑨=⑩。

（设计意图：在此环节中，教师引导学生分组通过剪一剪、拼一拼、画一画的方式开展自主探究和小组合作交流，培养学生的自主探究能力和合作交流能力。）

［案例二］平行四边形面积

1.经历转化，探究平行四边形面积公式

出示课件：村长慢羊羊年岁渐长，无力将村庄草地划分给村民，将划分权交给灰太狼。但是分完后，喜羊羊和懒羊羊分别得到一块平行四边形草地和长方形草地，双方因为草地面积争论不休，这可怎么办？你能够帮喜羊羊和懒羊羊对比各自分到的草地面积吗？

师：根据我们之前所学的割补法、数格子法，你能够比较喜羊羊和懒羊羊分到的草地面积吗？

生A：通过数格子方法可以数出来他们都分到了18平方米的草地。

生B：用割补法，可以把平行四边形转化为长方形，也可以发现两块草地的面积一样。

师：请大家观察表格中的数据，你有怎样的发现？（见表4）

生A：我发现喜羊羊和懒羊羊分到的草地中，喜羊羊草地的底和懒羊羊草地的长一样长，喜羊羊草地的高和懒羊羊草地的宽一样长。

师：按照之前我们所学的长方形面积公式为S长方形=长×宽，那你们能够推出平行四边形的面积公式吗？

生A：S平行四边形=底×高。

（设计意图：此环节主要通过例题引导学生思考长方形与平行四边形的关联，感受图形转化的过程，同时通过长方形面积公式猜想平行四边形面积公式，培养知识的迁移应用能力。）

2.自主探究，验证平行四边形面积公式

师：请同学们自行分为4人制小组，利用身边的工具验证平行四边形的公式。

学生分组探究、展示。

A组：我们小组用卡纸剪出了一个平行四边形，把平行四边形分成了一个三角形和梯形，通过变换位置拼成了一个长方形。

师：那图形变换后，有哪些变化吗？

A组：图形的整体面积没有变化，只是图形的形状变了。

师：有其他小组要补充的吗？

B组：变换后，长方形的长相当于平行四边形的底，宽相当于高。

师：那能够用长方形的面积公式推导出平行四边形面积公式吗？

组A：转化后的平行四边形成为一个长方形，长方形的长和宽对应平行四边形的底和高，而S长方形=长×宽，所以S平行四边形=底×高。

（设计意图：此环节通过小组合作，引导学生集思广益，通过剪一剪、拼一拼、挪一挪的方法将平行四边形转化为长方形，同时通过实际测量、观察、讨论发现长方形和平行四边形的关系，并通过长方形的面积公式推导出平行四边形的面积公式。整个过程，学生感受了图形转化，体会了数学转化思想。）

五、发挥教学价值，做好教学反思

基于“大概念”的小学数学大单元教学实践中，学生对单元知识的掌握效果得到显著提升。以此次“多边形的面积”大单元教学为例，以大概念“转化思想”为引导，学生掌握了长方形、平行四边形面积公式及推导过程，并在推导过程中感受了数学转化思想。除此之外，大单元教学过程中學生能够利用所学的多边形面积计算公式解决实际的数学问题，建立了数学学习与生活实际的联系，感受到数学的学科价值。但是此次教学实践中仍有部分不足，如对“大概念”“大单元”数学教学分析不够透彻，导致学习活动开发不够完善，今后的教学实践中将继续深化“大概念”“大单元”教学理念，设计出体现“大概念”“大单元”教学特色的学习活动。

（作者单位：西峰区什社乡什社小学）

编辑：张俐丽