基于核心问题培养模型意识

张馨月

教师以苏教版数学三年级上册“植树问题”一课教学为例，基于核心问题，引导学生通过观察、猜测、推理等活动，自主探索出植树问题的数学模型，并尝试运用该数学模型来解决生活中的实际问题，以此达到培养学生模型意识的目的。

一、多维整合分析，提炼核心问题

核心问题既是一节课的“课眼”，也是一节课的核心任务。聚焦核心问题，既是指引学生正确学习方向的自然选择过程，也是课堂教学活动的价值体现。笔者结合多年的实践探索，认为应通过教材的问题、教师的问题和学生的问题三个层面进行分析，其中，教材的问题是根本点，是对数学本质理解的知识性问题；教师的问题是着力点，是指能够引导学生自主建构知识和积极思维的问题；学生的问题是切入点，是指学生结合已有知识经验，针对新知提出的本源性问题或疑难问题。

教材的问题：在苏教版教材中，一改植树问题中建构“点与段的关系”模型为“找规律”，着重让学生在理解“一一间隔排列”的基础上发现并理解“看头尾”法比较一一间隔排列中两种物体数量的规律。这样以“一一对应”的思想来帮助学生建立“点段”模型，从而解决植树问题。

教师的问题：如何让学生感受和体验生活中的间隔现象？进而从这些生活现象中构建出数学模型。

学生的问题：本课知识对于学生而言，都是生活中的间隔现象，学生虽然比较熟悉，但未经过一个系统的梳理和“数学化”的过程。他们思考问题的重點聚焦在生活中的间隔现象究竟有什么规律？

围绕以上三个层面，笔者提炼出核心问题：间隔排列的规律是什么？

二、呈现核心问题，感知“植树”模型

以核心问题，引导学生充分感知，积累表象，感知数学模型，是培养数学模型意识的基础。

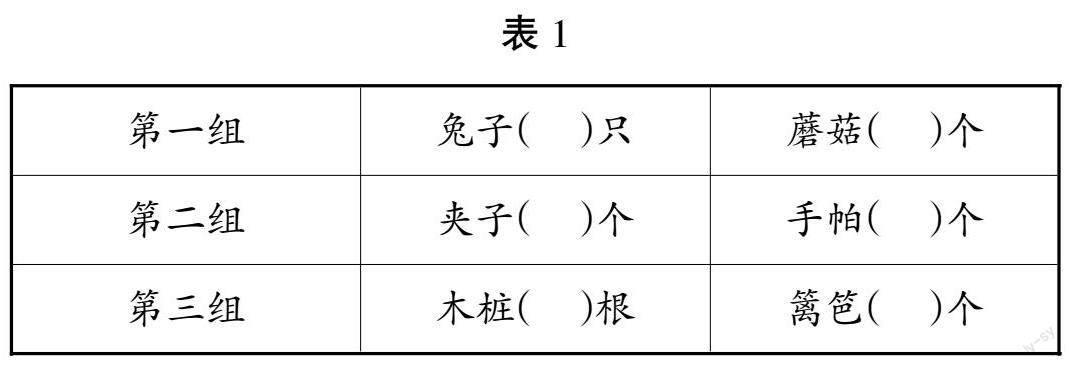
呈现教材78页的插图（见图1），提出核心问题：森林里的景色真美啊！小兔子在草地上跳着舞，小小的手帕在空中迎风飘扬，小路边郁郁葱葱的树木，红蓝相间的花朵竞相开放。图中的小兔与蘑菇是怎样排列的？

生1：一只兔子，一朵蘑菇，又一只兔子，一朵蘑菇，这样排列下去的。

生2：可以把一只兔子和一朵蘑菇看作一组，一组一组地出现。

师：是的，像这样两只兔子间隔着一朵蘑菇，两朵蘑菇间隔着一只兔子，相间排列，就叫作“一一间隔排列”。

三、聚焦核心问题，建构“植树”模型

（一）观察情境，了解“一一间隔排列”的特征

师：再次观察图片，你还能发现什么吗？

生1：手帕和夹子是一一间隔排列，一个夹子，一块手帕，这样排列下去。

生2：木桩和篱笆是一一间隔排列，一个木桩，一个篱笆，这样进行排列。

师：的确，这两组物体也是一一间隔排列的。你们还能发现什么特点吗？

生3：两边的事物是相同的。

师：咱们来具体看一看。

此处重点学生表达：前面是（  ），后面是（  ），中间是（  ）。在第一组图形中，前面是兔子，后面是兔子，中间是蘑菇，因此，兔子为两端物体，蘑菇排在中间把兔子隔开为间隔物体。学生仿照说一说另外两组中的两端物体和间隔物体。

师：同学们，你们能比一比这三幅图里两种物体的数量吗？你有什么新发现吗？

学生填写表格1，分析数量之间的关系，并分享交流自己的发现。

生4：两边的比中间的要多1个。

师：你能说得更具体一点吗？

生4：第一组图中，兔子8只，蘑菇7个，所以兔子的数量要比蘑菇的多1个；第二组图中，夹子10个，手帕9个，所以夹子的数量要比手帕的多1个，同样，第三组图中，木桩13个，篱笆12个，木桩比篱笆的数量要多1个。

师：能说说你的发现吗？

生4：我发现两端物体的数量比中间间隔物体的数量多1个。

（二）比较归纳，探索两端相同的间隔排列两种物体数量之间的关系

师：同学们，请你们想一想，为什么会“多1”呢？

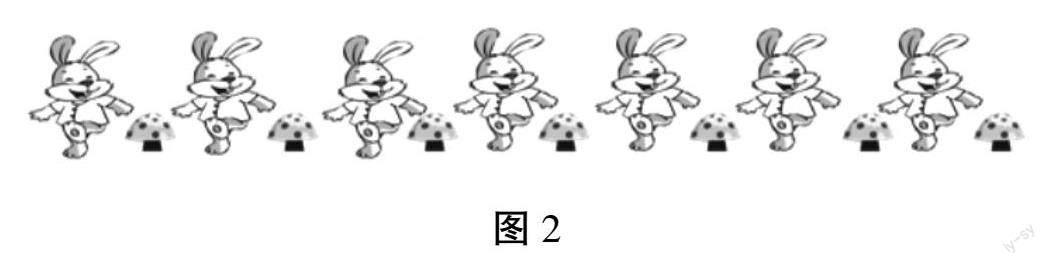
学生自主思考，但大部分学生都是从数量上给出了“多1”的结论，却无法说清楚缘由。为此，笔者继续引导学生对比观察图2和图1，并说一说它们之间有什么不同。

生：图2中的一只兔子对应着一朵蘑菇，兔子和蘑菇的数量同样多，但图1中最后一只兔子没有蘑菇对应，所以兔子比蘑菇多1。

教师利用课件隐去了图2中的蘑菇，只留下兔子，如图3所示。

师：这幅图又有了变化，现在只剩下兔子，但兔子与兔子之间出现了什么呢？

生1：出现了间隔。

师：看一看兔子之间的间隔数，你能发现什么？

生2：兔子和蘑菇本来是一一对应的，但最后一只兔子没有了对应，所以，兔子比间隔数多1。

生3：可以把空着的地方想象成蘑菇，这样就跟图2的情况一样了。

师：那图1中其他两组排列里也是这种现象吗？咱们来看一看。

师：一个物体有规律地摆放，也可以当作物体与间隔之间的一一对应。

从前面的学习我们可以发现，当兔子和蘑菇依次摆放，当它们完全对应时，兔子和蘑菇的数量是相等的；当不完全对应时，只要第一个和最后一个都是兔子，兔子的数量就要比蘑菇的数量多1。

师：图1中其他两组排列里也是这种现象吗？咱们来看一看。

生1：第二组中，排列的两端都是夹子，中间间隔物是手帕，所以，由于两端物体要比中间间隔物体多1，所以，夹子的数量比手帕多1。

生2：第三组中两端相同，排在两端的物体比中间多一个，木桩是排在两端的，所以就多了一根木桩。

师：像图1这样晒手帕，晒15块手帕需要几个夹子？20只小兔站成一排，每两只小兔中间有一个蘑菇，一共有多少个蘑菇？你能不计算就得出结果吗？

学生自主探究、仔细观察，并运用前面得出的结论进行分析，很好地促进了学生对“植树”模型的初步构建。

（三）动手操作，进一步完善对间隔排列的兩种物体数量关系的认识

师：在平时的生活中，你见过上述一一间隔排列的现象吗？

学生提出电线杆、锯木头、种树等生活现象，在分享交流中进一步巩固间隔排列中“一一对应”的分析方法。

师：你能用你喜欢的数字、图形或字母创造一个“一一间隔排列”吗？

学生自主创造，完成表2，并小组分享自己的成果。

学生从表格中发现：两种物体一一间隔排列，它们在数量上只有两种情况，可能多1，也可能相等。

（四）迁移升华，构建“植树问题”模型

1.对比分析，厘清点、段

从间隔问题“物与间隔”上升到植树问题中的“点与段”，首先需要学生厘清点与段的概念。

问题1：30米的一段公路，每5米一段，一共分为几段？

问题2：30米的一段公路，每5米种一棵树（两端要栽），一共可以种几棵树？

对于问题1，大部分学生给出的答案是：30米长的小路，每5米分成一段，可以分为6段。但有少部分学生得出了如下答案：30÷5=6，6+1=7。

师：为什么会选择用除法进行计算呢？

生1：每5米一段。

师：这句话说明了什么呢？

生1：是将这段公路进行平均分。

由此可见，生1将平均分的问题等同为“植树问题”，这也是学生在学习植树问题时经常犯的错误。

对于问题2，大部分学生利用画图的方式，最后给出的答案是：30米公路，每5米种一棵树，可以先把30米分成6段，由于头尾都要种树，所以需要加上1棵，即6个间隔种7棵树。

师：你们觉得问题1和问题2有什么异同之处？

生2：相同点：都是30米公路。

生3：在计算时都要做除法，30÷5=6。

师：那它们的不同之处在哪里呢？

生：问题1只需要做除法，而问题2还需要进一步做加法计算。

师：这是为什么呢？

生：树是种植在段与段相交的点上？

师：那么一段有几个点呢？两段有几个点呢？三段？四段呢？点与段之间有什么关系呢？

学生自主探究，结果发现在平均分的除法里面，点比段多1。

2.迁移运用，强化模型运用

习题1：沿河岸的一边共栽了50棵柳树，每相邻两棵柳树中间栽一棵桃树，可以栽（  ）棵桃树。

习题2：池塘一周种了100棵柳树，还要再种上一些桃树，和柳树一一间隔排列，那要种多少棵桃树呢？

习题3：五路公共汽车行驶路线全长12km相邻两站之间的路程都是2km。一共设有多少个车站？

（五）教学总结

本节课要建立的模型即：一一间隔排列两种物体头尾相同则数量相差1，头尾不同数量相等。整个教学过程，基于核心问题为学生提供独立思考、动手操作、合作探究、展示交流的时间和空间。学生从中经历了提出数学问题—解决数学问题—发现数学规律—建构数学模型的过程。

1.“植树问题”一课，对于学生来说最主要的难点就在于：为什么要在“间隔数”的基础上，或者“＋1”或者“－1”，又或者“不加不减”？为了让学生能厘清这个主要的难点，笔者的设想是：以核心问题为驱动，利用具体事物帮学生理解“间隔”，初步学会根据全长与间距求出“间隔数”，最后通过自主探究的方式，让学生充分理解植树的方式决定了植树棵数与间隔数的对应关系。

2.植树问题中转化思想的渗透，主要体现在由解决基本问题的“线”转化到能解决类似植树问题的“面”来研究，让学生进一步体会现实生活中的许多相似的现象，它们都可以利用“植树问题”模型来解决，从而感悟数学建模的重要意义。

（作者单位：宿迁市苏州外国语学校）

编辑：陈鲜艳