箱式挡浪结构透空堤消浪性能数值模拟

桂劲松，夏 曦

（大连海洋大学，辽宁大连 116023）

0 引 言

当前，各国越来越重视海洋生态环境的保护。相较于传统的重力式直立堤[1]、抛斜坡堤[2]等结构对海洋生态造成的破坏[3]，透空式防波堤[4]由于其下部透水，便于港内外水体交换，在海洋环境保护方面具有明显的优势，目前已逐渐发展成为一种重要的海洋工程结构。

最早对透空堤的研究主要针对单挡板透空堤。上世纪50 年代，Uresll[5]研究了无限水深情况下单挡浪板透空堤的透射效果，该理论研究对挡板式透空堤的发展有着深远影响。单侧挡浪板结构简单，易于施工，然而对于波浪的掩护作用较为有限。近年来许多学者对不同挡浪板结构开展了研究，周效国等[6]根据波能分布位置研究了不同层数和不同高程的开孔多层直立式挡板的消浪特性，总结出消浪效果好的挡板布置方案；Chioukh等[7]考虑正向入射的规则波，分析了双挡浪板透空堤的透射和反射系数；杜沛霖等[8]研究了带有透浪通道的直立式透空堤的消浪特性，由于波浪在透浪通道中多次的反射及绕射消耗了大量波能，达到了良好的消浪效果；Koraim 等[9]研究了双侧直立式挡浪板透空堤在波长以及结构尺寸变化时的水动力特性，并且建立了基于特征函数的理论模型；邵杰等[10]通过物理模型试验，研究了不同结构型式的双垂直挡浪板透空堤的透射系数，并指出透射系数随挡浪板入水深度的增大会显著减小；蔡丽等[11]研究了V形挡板式透空堤透射后的波高分布情况，结果表明，V形挡板透空堤对短周期波有很好的掩护作用；范骏等[12]针对双挡浪板透空堤进行了物理模型实验，不仅考虑了挡浪板入水深度和水平板板宽等因素对透射系数的影响，还对透浪系数的计算方法进行了研究；Li等[13]研究了水平单弧形板的波浪透射、反射、波压以及弧板周围流场变化；徐宁等[14]探究了双层水平板透空堤的透浪效果，发现相对板宽是影响结构透射和反射的主要因素；王丽雪等[15]对比了双层水平板和双层弧形板的透射效果，发现弧形板各方面性能均优于水平板。

以上学者大多是对水平或垂直板透空堤消浪结构进行了研究，但对于水平板和垂直板组合的箱式挡浪结构透空堤的研究却鲜有报道。本文基于粘性流理论对比了垂直立板式透空堤和箱式透空堤的消浪特性，并且深入探究了箱式透空堤的水动力特性，揭示了箱式透空堤的消浪机制。

1 数值模型建立

本文基于OpenFoam 求解器建立数值波浪水槽，采用有限体积法对空间离散，应用PISO 算法迭代求解压力及速度，应用动边界法模拟推板造波，在数值波浪水槽的末端设置阻尼消波区。

1.1 控制方程

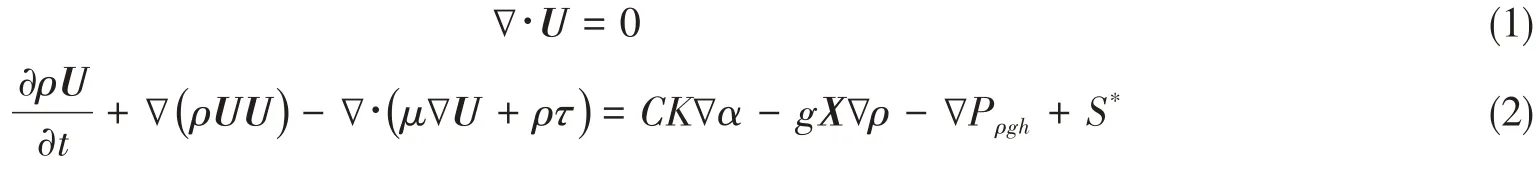
式中，U为平均速度矢量，ρ为二相流的平均密度，t为时间，μ为二相流平均动力粘度，ρτ为雷诺应力项，其中τ表示由脉动值引起的雷诺应力张量。CK∇α为表面张力项，其中C为表面张力系数，一般取为0.07 kg/s2，K为自由面的曲率，α为相体积分数，g为重力加速度，X为位置矢量。Pρgh是为了求解方便引入的压力项，S*为动量消波源项。

1.2 VOF 法追踪自由表面

对不可压气液二相流模型，VOF法可根据两相流在网格中所占比例来确定自由面流体变化，该流体的密度ρ和动力粘度系数μ由以下体积分数函数表示：

式中，ρ1为水的密度，ρ2为空气的密度，μ1为水的动力粘度系数，μ2为空气的动力粘度系数。

1.3 边界条件

本模型主要是固壁边界条件，速度场在边界满足不可滑移条件：

压力场在壁面处满足压力沿法向方向的梯度为0的条件：

1.4 造波与消波

本文采用动边界法来模拟实验室的推板造波，根据线性理论得出规则波波高与推板冲程的关系为

式中，Hi为入射波高，S为造波机造波板冲程，k为波数，d为水深。推板的位移X和速度U分别为

根据以上推板的位置和速度公式可以得到推板线性波波面表达式为

式中，ω是波浪频率，x表示推板位置。

消波方法由Larsen等[16]提出，在动量方程中添加源项，使波浪在阻尼区中逐渐衰减。

式中，S*为动量消波源项，u为速度矢量，χ为衰减函数。本文中衰减系数取为5，阻尼区长度取为1～2倍波长。

2 数值模型验证

2.1 理论验证

数值波浪水槽利用项目组前期研发的基于OpenFoam 的DUTFoam 求解器[17]模拟，尺寸为：长21.7 m、宽0.7 m、高0.8 m，水深为0.3 m，波浪参数为：波高Hi=0.08 m，周期T=1.8 s，阻尼区取2 倍波长。水槽中共放置四个浪高仪，位置分别在2 倍波长、3 倍波长、1/2 阻尼区和水槽末端处放置，将其依次编号为WG1、WG2、WG3和WG4，图1 为数值水槽示意图。首先本文对数值模型的网格收敛性进行了验证，选择四种尺度的网格计算了波面变化，网格参数如表1所示。

表1 网格参数Tab.1 Mesh parameters

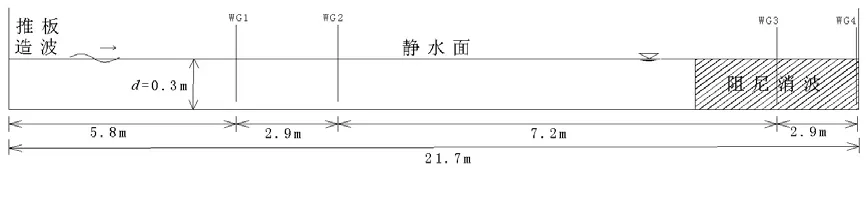
图1 数值水槽示意图Fig.1 Schematic diagram of numerical flume

图2 为空水槽时在结构物处的四种不同网格尺度所计算的波面结果，由图可知当网格尺度为0.01 m×0.005 m×0.005 m（长×宽×高）和0.008 m×0.004 m×0.004 m（长×宽×高）时波面已平稳，表明网格已收敛。考虑到计算效率等问题，本文选取0.01 m×0.005 m×0.005 m 作为网格尺度。图3为波面模拟结果和微幅波理论结果对比。由图可知，在x=5.8 m和x=8.7 m位置的波面和理论波面吻合较好。图3（c）～（d）是阻尼区中间处水槽末端波面与理论波面的对比图，可以看出水槽末端的阻尼消波区具有较好的波浪衰减作用。综上所述，理论上数值水槽具有有效性。

图2 不同网格尺度的波面历时曲线比较Fig.2 Comparison of wave surface duration curves with different grid scales

图3 微幅波波面和数值模拟波面对比图Fig.3 Comparison of airy wave surface and numerical simulation wave surface

2.2 物模验证

在结构物前后各放置两个波高仪测量入射、反射和透射波高，计算透射系数Kt和反射系数Kr。

式中，Ht为透射波高，Hi为入射波高，由Goda两点法[18]分离出反射波高Hr。

物理模型主要由前挡浪板和后挡浪板组成，前后挡浪板的固定尺寸为0.7 m×0.3 m×0.025 m。试验采用波浪周期T=1.8 s，波长L=2.88 m，Hi=0.06 m，采用DS30波高水位测量仪和DJ800多功能检测系统测量和采集波面数据。

图4为数模试验时的模型简图。在进行物模试验和数模试验对比验证时，采用图4中无水平底板的结构，物模试验中采用的小直径桩对流场等水动力影响较小，数模时忽略。

图5为物理模型试验的布置简图，水槽长为40 m，结构物放置在水槽中后方，在结构物前方2 m和3 m处各放置两个浪高仪，在结构物后方1 m和2 m处各放置两个浪高仪。

图4 数值水槽模型简图Fig.4 Numerical flume model diagram

图5 物理试验布置图Fig.5 Layout of physical test

图6 是T=1.8 s、d=0.3 m，Hi=0.06 m 时物模波面与数模波面入射波、反射波和透射波的对比结果。反射波为WG1和WG2测得的合成波采用两点法分离后的波面，透射波为WG3的波面，WG3测得的透射波和WG4测得的透射波基本一致，故在本文中只选择了WG3波面进行对比。

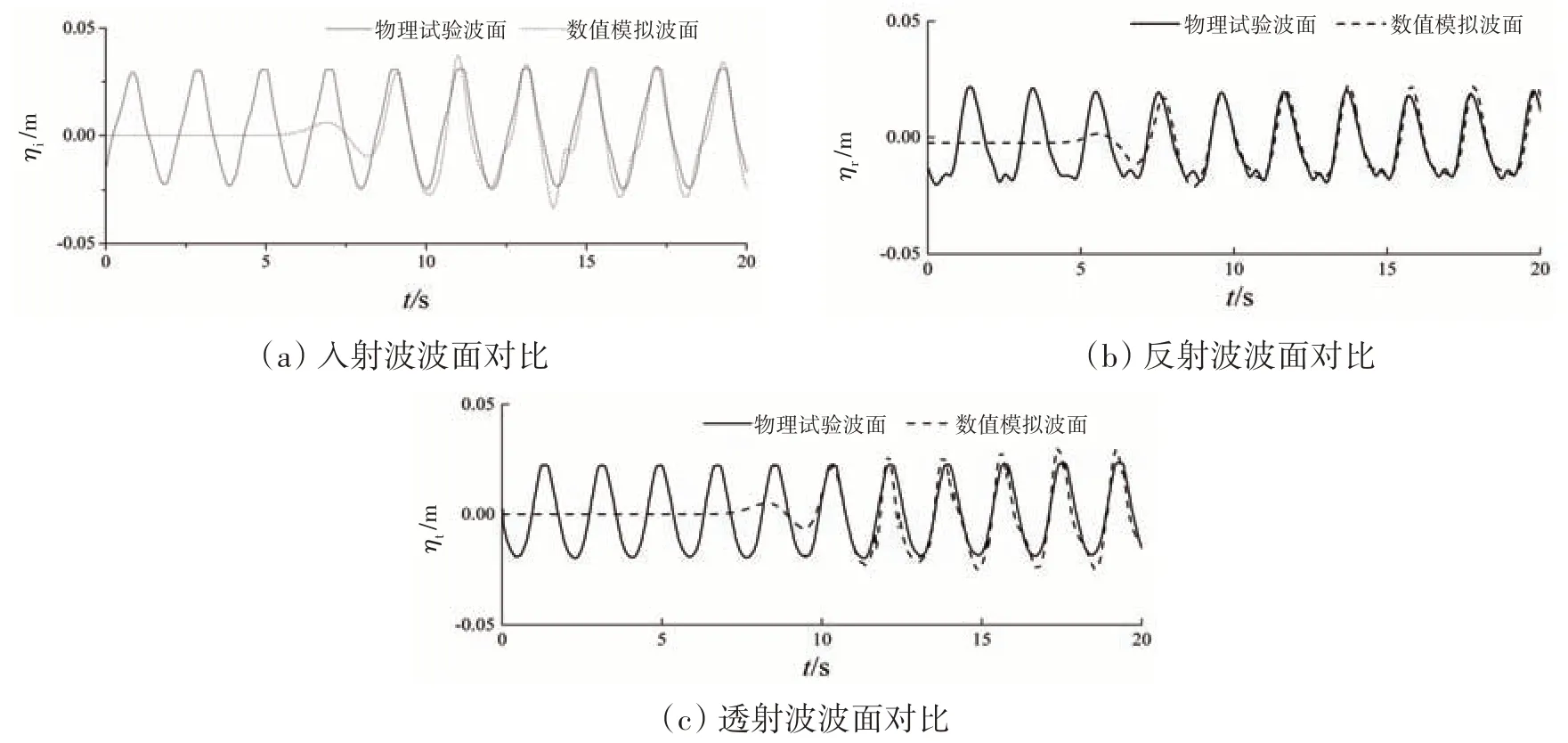
图6 波面对比图Fig.6 Wave surface contrast diagram

图7 透射系数和反射系数物模数模对比Fig.7 Modulo-digital comparison of transmission coefficient and reflection coefficient

图7 为d/L=0.1、0.17、0.21（d为水深，恒为0.3 m，L为波长），波高Hi=0.06 m 时，前挡浪板入水深度0.5Hi，后挡浪板相对入水深度不同时，物理试验和数值模拟的透射系数和反射系数对比图，横坐标为相对入水深度Δ/d（Δ为后挡板入水深度）。

由图6～7可见，波面曲线、透射系数、反射系数的数模和物模结果基本吻合，验证了数值水槽的有效性。

3 数值模型结果与讨论

3.1 垂直挡板和无底板箱式结构对比

图8为数值模拟的结构网格图。

图8 结构网格图Fig.8 Structural grid diagram

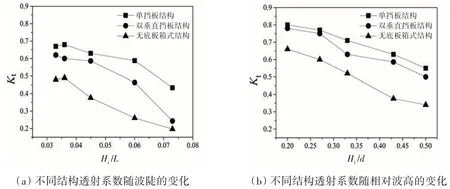
图9 透射系数变化图Fig.9 Diagram of transmission coefficient changes

图10 反射系数变化图Fig.10 Diagram of reflection coefficient changes

图9比较了Hi/L（Hi为入射波高）为0.033～0.073，Hi/d为0.2～0.5时3种不同结构挡板透射系数变化趋势。结果表明：单挡板结构透射系数最大，双垂直挡板结构透射系数小于单挡板，波高变化时表现不明显，波长变化时表现较为明显，最大可减小45%，最小可减小12%。无底板箱式结构透射系数在3种结构中最小，对短周期入射波消浪效果更好，比双垂直挡板透射系数最大可消减35%。图10 比较了3种不同结构挡板反射系数变化情况。结果表明：单挡板结构反射系数最小，无底板箱式结构反射系数最大，其波高不同时反射系数增大得更为明显，最大可增加70%，最小可增加60%。

无底板箱式结构在半封闭区域内形成了消浪室，其消浪室内上面为空气，下面为水。图11 为同一位置双垂直板内和无底板箱式结构消浪室内气压变化情况，由图可见，消浪室内波浪受到气压的影响，压强变化明显。图12为同一位置双垂直板内和消浪室内波面位移变化情况，由图可见，当波浪经过无底板箱式结构时，消浪室内波浪受到气圧影响，波面位移明显较小。

图11 气压随时间变化Fig.11 Pressure varying with time

图12 结构内波面位移随时间变化Fig.12 Wave surface displacement varying with time

耗散系数是衡量波能消耗的系数之一，波能耗散系数定义如下：

式中，Kt为透射系数，Kr为反射系数，Kd为耗散系数

图13比较Hi/L为0.033～0.073，Hi/d为0.2～0.5时3种不同结构挡板耗散系数。结果表明：双垂直挡板耗散系数较大，无底板箱式结构耗散系数较小，在波陡较大和相对波高较大时其耗散相差较小。由图12可见，两种结构内波高相差较大，双垂直挡板和单挡板由于无水平顶板约束，不受消浪室内气压的影响，波浪上下震荡幅度较大，耗能相对较大；增加水平顶板，波浪受气压影响，上下震荡幅度变小，能量不能充分消耗，耗能相对较小。耗散系数随波陡的增加而减小，随相对波高的增大而增大。无底板箱式结构透射系数较小，但能量耗散较差，所以在结构中增加了水平底板，探究箱式透空堤的消浪特性。

图13 耗散系数变化图Fig.13 Diagram of dissipation coefficient changes

3.2 箱型板式透空堤水动力分析

图14为数值模拟的箱型板式结构网格图。

图14 箱型板式结构图Fig.14 Structural diagram of box-type structure

在结构中增加水平底板，上水平顶板和水平底板中间为空心结构，水平板厚度均为0.02 m,结构宽度B=0.7 m。在水面上方1.0Hi（入射波高）、水面上、水下0.5Hi和水下1.0Hi的位置增加水平底板。

图15比较了B/L为0.175～0.4时水平底板在不同位置，透射系数和反射系数随相对板宽（B/L）的变化。结果表明,相对板宽对结构透射系数和反射系数影响显著，相对板宽为0.19～0.4 时透射系数随相对板宽的增加而减小，但同时反射系数随相对板宽的增加而增大。对比不同结构，随着水平底板高度的降低透射系数随之减小，当底板放置在水面和在空气中时透射系数减小，幅度相对较小，底板在水下0.5Hi和1.0Hi时透射系数减小，幅度相对较大，而底板在水下1.0Hi时透射系数最小，与无底板结构透射系数相比最大可减小20%。反射系数随水平板高度的降低而增大，底板在水下1.0Hi时反射系数最大。综合可见，增加底板后的箱式透空堤消浪效果对长周期波和短周期波都适用。

图15 透射系数、反射系数随相对板宽的变化Fig.15 Transmittance coefficient and reflection coefficient varying with relative plate width

图16 透射系数、反射系数随相对波高的变化Fig.16 Transmittance coefficient and reflection coefficient varying with relative water height

图16 比较了Hi/d为0.2～0.5 时水平底板不同位置处透射系数和反射系数随相对波高的变化。结果表明，相对波高对结构透射系数和反射系数的影响较为显著，透射系数和反射系数随相对波高的增加而减小。对比不同结构，随着水平底板高度的降低透射系数随之减小，底板在水下0.5Hi和1.0Hi时透射系数减小幅度相对较大，而底板在水下1.0Hi时透射系数最小，相对于无底板结构透射系数最大可减小15%。反射系数随水平板高度的降低而增大，底板在水下1.0Hi时反射系数最大。综合可见，增加底板后的箱式结构透空堤对大的波高掩护效果更好。

图17 比较了B/L为0.175～0.4，Hi/d为0.2～0.5 时水平底板不同位置耗散系数的变化。结果表明，增加水平底板且底板放置在水中，结构耗散系数较大。水平底板放置在水中时会约束水质点的竖向运动，消耗更多能量。

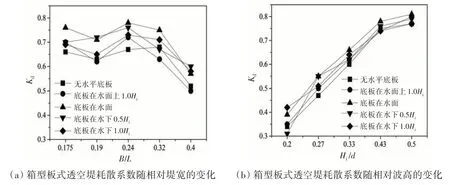
图17 耗散系数变化图Fig.17 Diagram of dissipation coefficient changes

水平底板放置在水中的位置对耗散系数影响较小，综合透射、反射和耗散系数，水平底板放置在水下0.5Hi和1.0Hi时透射较小，反射和耗散较大，消浪效果更为显著。

3.3 流场对比

图18～19 分别为周期T=1.8 s，无底板箱式结构和箱式结构在水下1.0Hi时的结构流场变化图。由图可见，对于无底板结构，波浪入射时，部分波浪进入消浪室内，虽有气压作用但消浪室内水质点竖向运动较为显著，使得透射波相对较大。增加水下水平板后，大部分波浪受到前挡板和水平板阻挡形成立波产生反射，透射的小部分波浪由于水平底板约束了水质点的竖向运动，从而达到良好的消浪效果。

图18 一个周期内无底板箱式结构流场变化图Fig.18 Flow field variation diagram of box structure without bottom plate in one cycle

图19 一个周期内箱式结构流场变化图Fig.19 Flow field diagram of box structure in one cycle

4 结 论

本文通过数值模拟对箱式挡浪结构透空堤消浪特性进行了系统的研究，主要结论如下：

（1）箱式挡浪结构透空堤透射系数随相对板宽的增加而减小，反射系数则相反。透射系数和反射系数均随相对波高的增加而减小。

（2）箱式结构水平底板位于水面以上时，由于消浪室内气压的影响产生耗散，耗散系数相对较小；水平底板位于水面以下时，由于水平底板约束水质点竖向运动产生耗散，耗散系数相对较大，消浪效果更好。

（3）箱式结构透射系数随水平底板高度的降低而减小，反射系数相反。