以GeoGebra软件为载体培育学生直观想象素养的教学实践

作者简介：祁山国宝（1979— ），男，一级教师，主要从事高中数学教学研究.

摘  要：采用探究实验，从“引导学生感知几何形态变化，发展空间想象能力”“指引学生寻觅动点运动规律，构建直观模型体系”“启迪学生发现数与形的联系，树立数形结合思想”等角度，分別阐述了在教学中以GeoGebra软件为载体培育和提升学生直观想象素养的路径.

关键词：直观想象；GeoGebra软件；核心素养；数学思维

一、问题提出

直观想象是六大数学核心素养之一.《普通高中数学课程标准（2017年版2020年修订）》指出，直观想象是借助几何的直观、空间的想象来感知事物的形态和变化，利用图形来理解与解决问题的过程. 其具体要求主要包括：能借助空间想象感知事物的位置关系和形态变化；能借助几何直观认识事物的运动规律；能构建数和形之间的联系，运用图形分析与探索数学中问题的求解思路.

直观想象要求学生能借形释数，能把抽象的、不易理解的数学学习对象用易于呈现的直观图形描述出来，对学生的思维习惯和空间想象能力要求较高. 在面对这些抽象的、不可视的数学对象时，学生往往无从下手. 因此，在讲授这些抽象的数学对象、发展直观想象素养时，教师如果单纯凭借板书教授知识很难达到理想的教学效果. 那么，在数学教学中发展学生的直观想象素养，我们应该怎样做才能更为有效呢？

把数学对象图形化、可视化，正是GeoGebra软件的强项，其恰好可以填补板书难以直观呈现抽象问题的缺陷. 利用GeoGebra软件，我们可以快速进行数和形之间的转化，可以方便地进行动态展现与演示，可以便捷地把抽象的内容形象化、具体化. 在数学课堂教学过程中，恰当使用GeoGebra软件能有效发展与提升学生的直观想象素养.

二、利用GeoGebra软件融合教学培育学生直观想象素养的实践

GeoGebra软件提供了很多便捷和实用的功能，借助这些功能我们可以快捷、准确地呈现几何对象间的位置关系，动态地展示几何元素间的变化规律，它为激活学生的探究热情、培育与提高学生的直观想象素养提供了强有力的支撑与保障. 下面介绍以GeoGebra软件为载体培育学生直观想象素养的一些实践.

1. 引导学生感知几何形态变化，发展空间想象能力

在二维平面上画空间图形，为了让图形更具立体感，有些线段长度和线线夹角会进行转变. 扭曲转变后的图形往往给学生学习与认识立体几何图形制造了视觉上的障碍. 因此，要提升学生的空间想象能力，单纯依靠粉笔和黑板会较难达到应有的效果. 而借助GeoGebra软件在展示立体图形方面的先天优势，就可以很好地克服这一困难. GeoGebra软件可以把立体图形各元素间的位置关系和各几何对象的形态变化展现得淋漓尽致，对丰富与拓展学生的空间想象能力有极大帮助.

例1  若正方体的各条棱长都等于1，且正方体每条棱所在的直线和平面[α]所成的角全部相等，则正方体被平面[α]所截得的截面面积的最大值等于（    ）.

（A）[334] （B）[233]

（C）[324] （D）[32]

答案：A.

该题要求学生具备较强的空间想象能力. 在求解过程中，学生可能会出现以下几个困惑：第一，平面[α]截正方体后得到的截面到底会出现哪些形状？第二，所有可能出现的截面形状中哪种面积最大？什么时候达到最大？

由于传统教学不能很好地展现与说明这一问题，所以我们引入GeoGebra软件，通过实验探究，引导学生直观感知立体几何截面形态的变化，培育学生的空间想象能力.

（1）探究实践，感知几何形态变化.

思考1：题目中满足已知条件的平面[α]截正方体所得的截面形状可能有哪些？

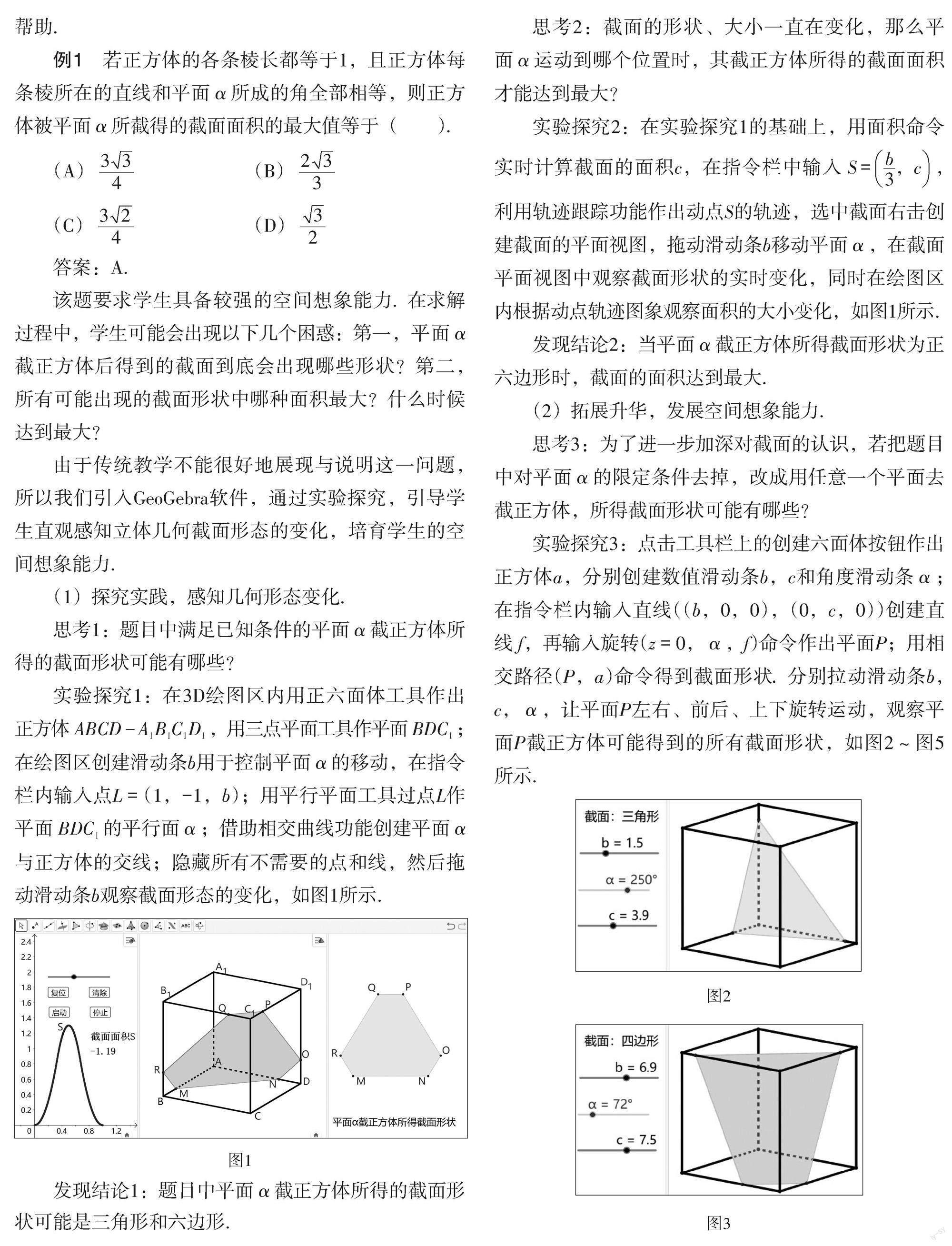
实验探究1：在3D绘图区内用正六面体工具作出正方体[ABCD-A1B1C1D1]，用三点平面工具作平面[BDC1]；在绘图区创建滑动条b用于控制平面[α]的移动，在指令栏内输入点L = （1，-1，b）；用平行平面工具过点L作平面[BDC1]的平行面[α]；借助相交曲线功能创建平面[α]与正方体的交线；隐藏所有不需要的点和线，然后拖动滑动条b观察截面形态的变化，如图1所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image5.png>

图1

发现结论1：题目中平面[α]截正方体所得的截面形状可能是三角形和六边形.

思考2：截面的形状、大小一直在变化，那么平面[α]运动到哪个位置时，其截正方体所得的截面面积才能达到最大？

实验探究2：在实验探究1的基础上，用面积命令实时计算截面的面积c，在指令栏中输入[S=b3，c]，利用轨迹跟踪功能作出动点S的轨迹，选中截面右击创建截面的平面视图，拖动滑动条b移动平面[α]，在截面平面视图中观察截面形状的实时变化，同时在绘图区内根据动点轨迹图象观察面积的大小变化，如图1所示.

发现结论2：当平面[α]截正方体所得截面形状为正六边形时，截面的面积达到最大.

（2）拓展升华，发展空间想象能力.

思考3：为了进一步加深对截面的认识，若把题目中对平面[α]的限定条件去掉，改成用任意一个平面去截正方体，所得截面形状可能有哪些？

实验探究3：点击工具栏上的创建六面体按钮作出正方体a，分别创建数值滑动条b，c和角度滑动条[α]；在指令栏内输入直线（（b，0，0），（0，c，0））创建直线 f，再输入旋转（z = 0，[α]，f）命令作出平面P；用相交路径（P，a）命令得到截面形状. 分别拉动滑动条b，c，[α]，让平面P左右、前后、上下旋转运动，观察平面P截正方体可能得到的所有截面形状，如图2 ～ 图5所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image7.png>[图2]<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image8.png>[图3]

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image9.png>

图4

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image10.png>

图5

发现结论3：用任意一个平面去截正方体，所得截面形状可能是锐角三角形、等腰三角形或等边三角形，但不能是钝角三角形或直角三角形；所得截面形状可能是梯形、平行四边形、菱形、矩形、正方形等四边形，但不能是直角梯形；所得截面形状还可能是除正五边形外的任意五边形，或者是任意六边形.

（3）感悟.

利用GeoGebra软件作图的优势是把截面形状生动地呈现出来，避免了学生单纯依靠纸笔的枯燥和空洞想象，使学生认识立体几何形态不再困难. 同时，GeoGebra软件直观动感的画面为学生认识立体几何创造了一个宽松、和谐、形象的学习氛围，這对激发学生探究立体几何的兴趣、建立空间观念和锻炼空间想象能力会起到有益的作用.

2. 指引学生寻觅动点运动规律，构建直观模型体系

直观模型的建立与成熟的经验需要时间的积累. 特别是在学生刚刚接触动点问题时，由于对直观模型缺乏经验，会感到陌生与匮乏，对动点轨迹问题无法形成有效的求解对策. 这时，如果引入GeoGebra软件，把动点的运动过程呈现出来，让学生领会“动”的本质和灵魂，不仅可以活跃课堂气氛，帮助学生积累实战经验，更能让“教”和“学”有机融合，取得事半功倍的效果.

例2已知圆[A： x+42+y2=100]，在圆内有一定点[B4，0]，点[P]是圆上的一个动点，若线段[BP]的垂直平分线与直线[AP]交于点[M]，求动点[M]的轨迹方程.

答案：[x225+y29=1].

这是一个动态问题，采用传统教学无法让学生感受运动变化的过程，不利于学生思维的发展. 而借助GeoGebra软件展开动态演示实验，直观展示图形的动态变化过程，可以让学生在探究过程中学会发现规律，提升模型意识.

（1）借助GeoGebra软件的跟踪功能，指引学生寻觅动点运动规律.

思考1：点[M]的运动是由点[P]引起的，那么当动点[P]在圆上运动时，点[M]在运动过程中始终会保持哪些数量关系？问题中刚好出现关于原点对称的两个定点[A]，[B]和动点[M]，我们学过的哪类曲线的定义刚好也用到“两定加一动”？受其启发，我们是否需要关注点[M]到[A]，[B]两点的距离之和（或差）的数值特征呢？

实验探究1：点击工具栏滑动条按钮创建数值滑动条a，用于控制点P的移动；在指令栏中分别输入以下命令：A = （-4，0），B = （4，0），圆A = 圆周（A， 10），P = 描点（圆A，a），BP = 线段（B，P），AP = 线段（A，P），n = 中垂线（BP），M = 交点（n，AP），右击点M设置显示轨迹；点击工具栏按钮工具分别创建4个按钮；按开始按钮，或拖动滑动条观察点M的运动轨迹，如图6所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image20.png>

图6

发现结论1：[MA+MB=PA=10=2a]，且[AB=][8=2c<10]，故动点[M]的轨迹是以[A]，[B]为左、右焦点的椭圆. 因为[b2=a2-c2=52-42=9]，所以点[M]的轨迹方程是[x225+y29=1].

（2）利用GeoGebra软件动态演示，引导学生将抽象问题直观化.

思考2：若改变点[B]的位置，让点[B]从左到右由圆外运动到圆内，再运动到圆外，则点[M]的轨迹形状是否会改变？若会改变，则可能出现的轨迹类型有哪些？

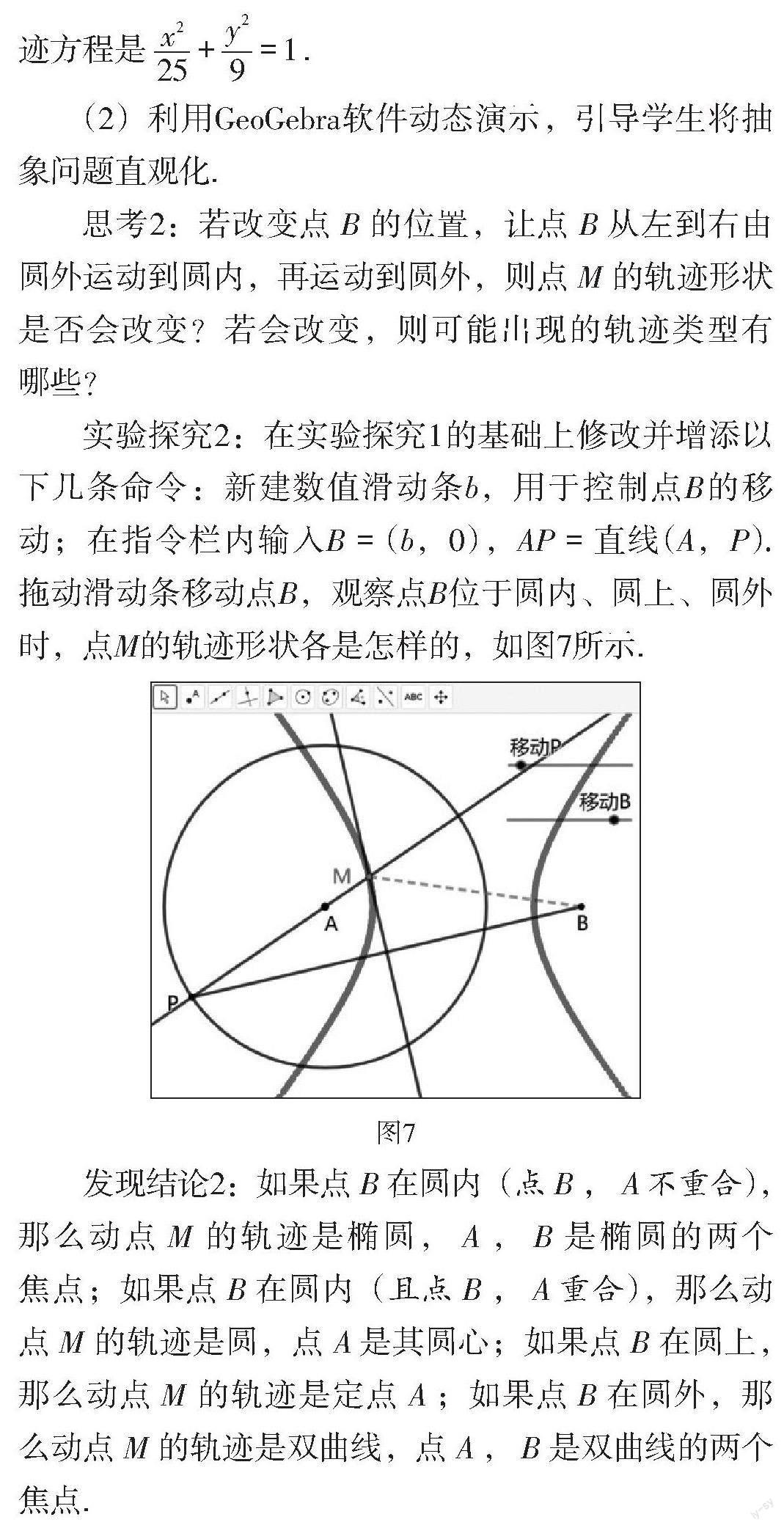
实验探究2：在实验探究1的基础上修改并增添以下几条命令：新建数值滑动条b，用于控制点B的移动；在指令栏内输入B = （b，0），AP = 直线（A，P）. 拖动滑动条移动点B，观察点B位于圆内、圆上、圆外时，点M的轨迹形状各是怎样的，如图7所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image26.png>

图7

发现结论2：如果点[B]在圆内（点[B]，[A]不重合），那么动点[M]的轨迹是椭圆，[A]，[B]是椭圆的两个焦点；如果点[B]在圆内（且点[B]，[A]重合），那么动点[M]的轨迹是圆，点[A]是其圆心；如果点[B]在圆上，那么动点[M]的轨迹是定点[A]；如果点[B]在圆外，那么动点[M]的轨迹是双曲线，点[A]，[B]是双曲线的两个焦点.

（3）追根溯源，挖掘椭圆背后蕴藏的光学特性.

思考3：再次回到例2，我们已经确定点P在圆上运动时点M的轨迹是以[A]，[B]为左、右焦点的椭圆. 在运动过程中，判断线段BP的中垂线n与这个椭圆的位置关系. 图中的两个焦半径MA和MB分别与中垂线n的夹角[α]和[β]具有什么数量关系？

实验探究3：在实验探究1的基础上新增实时计算角度[α]和[β]的命令、新建数值滑动条. 通过拖动滑动条跟踪线段BP的中垂线n的运动，观察线段BP的中垂线与这个椭圆的位置关系，以及角[α]和[β]的数量关系，如图8所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image29.png>

图8

发现结论3：运动过程中，线段BP的中垂线与这个椭圆始终保持相切，角[α]始终等于角[β]. 因此，通过验证可以得到椭圆在光学上的一个特性，即从椭圆的一个焦点发出的光线，在受到椭圆反射后，它的反射光线一定过椭圆的另一个焦点.

（4）感悟.

借用GeoGebra软件描述动点问题，可以让我们“纸上谈兵”，为乏力无味的课堂增添灵气，可以让学生面对动点问题时不再感到畏惧和束手无策. GeoGebra软件为学生发现运动的逻辑与规律、构建直观模型体系奠定了基础和保障，也激发了学生的好奇心，提升了课堂教学效率，有助于学生更好地理解和应用直观模型.

3. 启迪学生发现数与形的联系，树立数形结合思想

利用GeoGebra软件作图，再通过滑动条改变参数大小，可以快速暴露和展现图形的变化过程及特征. 借助GeoGebra软件在“形”中探究数的关系，在“数”中发现形的特征，可以把“数”和“形”十分和谐、有效地融合到一起. 在这方面，传统的黑板教学无法与之相比. 通过GeoGebra软件鼓励学生进行探究和实验，启迪学生发现和挖掘“数”与“形”的联系，可以有效提升学生利用数形结合思想转化问题的能力.

例3 （1）已知[M]是圆O：[x2+y2=9]上的一个动点，圆O的直径为[AB]，且点[M]不与点[A]，[B]重合，直线[MA，MB]的斜率分别为非零的[k1，k2]，求[k1k2]的值.

（2）已知[M]为椭圆[x24+y23=1]上的一个动点，椭圆的左、右顶点分别为[A，B]，且点[M]不与点[A，B]重合，直线[MA，MB]的斜率分别为非零的[k1，k2]，求[k1k2]的值.

经过计算，容易得到第（1）小题的答案为k1k2 =[-1]，第（2）小题的答案为k1k2 =[-34]. 具体过程省略，但解题过程引发我们产生如下思考.

上述两个问题具备如下共同特征：计算出来的两条直线的斜率之积都为定值，且点[A]，[B]都是曲线上关于原点中心对称的两个点，点M都是曲线上除[A]，[B]外的动点. 因此，让我们产生如下疑问.

（1）对于任意的椭圆，如果满足上述特征，那么直线MA，MB的斜率之积是不是都为定值？

（2）如果关于原点中心对称的两个点A，B也在曲线上运动，那么直线MA，MB的斜率之积是不是一定为定值？

（3）若直線MA，MB的斜率之积都为定值，点A，B及点M的运动是否会改变其定值的大小？椭圆的形状是否会影响其定值的大小？能够影响这一定值大小的因素是什么？

带着这些疑问，我们提出如下问题，同时借助GeoGebra软件展开实验探究，强化学生的数形结合意识.

问题：已知点[M，A，B]是椭圆[x2a2+y2b2=1 a>b>0]上的动点，点A，B关于原点对称，且点[M]不与点A，B重合，直线[MA，MB]的斜率分别是非零的[k1，k2]，判断[k1k2]是否为定值？如是，予以证明.

（1）实验探究，用“形”探寻规律.

实验操作：利用滑动条工具作数值滑动条a，b，c，分别用于控制参数a，b的大小和点M的移动. 作角度滑动条[α]，用于控制点A，B的运动. 在指令栏内分别输入椭圆m：x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1，直线n：y = （tan[α]）x，A = 交点（椭圆m，直线n，2），B = 交点（椭圆m，直线n，1），M = 描点（椭圆m，c），直线MA：直线（M，A），直线MB：直线（M，B）. 用斜率运算指令分别算出直线MA和直线MB的实时斜率. 接下来，我们分别展开下列探究，并分析、观察图象中数据的变化规律，如图9所示.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image44.png>

图9

学生探究1：保持其他参数值不变，拖动滑动条改变点A，B的位置，观察直线MA，MB的斜率之积，看是否发生改变.

探究结论1：点A，B的位置变化并没有引起斜率乘积[kMAkMB]的变化，说明[kMAkMB]的值与点A，B的位置无关.

学生探究2：保持其他参数不变，拖动滑动条改变点M的位置，观察直线MA，MB的斜率之积[kMAkMB]，看是否有变.

发现结论2：移动点M改变不了斜率之积[kMAkMB]的大小，说明[kMAkMB]的值与点M的位置无关.

学生探究3：保持A，B，M三点的位置不动，利用鼠标拖动滑动条改变参数a的大小，看[kMAkMB]的值是否变化. 再保持其他参数不变，只改变参数b的大小，观察[kMAkMB]的值是否变化.

发现结论3：参数a，b中任何一个值的改变都会引起直线MA，MB的斜率之积发生变化，说明[kMAkMB]的值是由参数a，b的值来共同确定的. 参数a，b的值一旦确定，直线MA，MB的斜率之积[kMAkMB]的值就必为定值.

发现这个规律后，我们能否通过逻辑推理来进行严谨地概括与证明？

（2）推理验证，用“数”证实规律.

根据上述实验探究结果可知：变动点A，B，M的位置，改变不了直线MA，MB斜率之积的值，斜率之积[kMAkMB]的大小只取决于参数a，b的值. 所以可以利用特殊值法，先找到定值，再证明其为定值. 我们把点A，B分别移动到椭圆的左、右顶点的位置，把点M移动到椭圆的上顶点的位置. 此时，有[A-a，0]，[Ba，0]，[M0，b]，利用斜率公式计算，易得[kMAkMB=][-b2a2]．由此，可以得到椭圆的如下性质.

椭圆性质：如果[M，A，B]是椭圆[x2a2+y2b2=1 a>b>0]上的动点，点[A，B]关于原点对称，且点[M]不与点[A，][B]重合，直线[MA，MB]的斜率分别是非零的[k1，k2]，那么[k1k2]为定值，且[k1k2=-b2a2]．

证明：根据点A，B关于原点中心对称，

设[Ax1，y1，Mx，y]，则[B-x1，-y1].

由点[A，M]在椭圆上，可得[x12a2+y12b2=1]，[x2a2+y2b2=1].

两式相减，得[x+x1x-x1a2+y+y1y-y1b2=0]，

即[y-y1x-x1 ? y+y1x+x1=-b2a2].

因为[kMA=y-y1x-x1]，[kMB=y--y1x--x1=y+y1x+x1]，

所以[kMAkMB=-b2a2].

（3）数形结合，用类比推广规律.

接下来，用数形结合类比上述椭圆性质的发现思路和证明方法（探究实验如图10所示），我们可以很容易验证此性质推广到双曲线中亦成立，证明过程略，性质内容如下.

<＼＼10.1.5.160＼g＼中数高中2023年飞翔＼中数高中2023年第12期＼高中2023年第12期＼Image＼国宝image64.png>

图10

双曲线性质：如果[M，A，B]是双曲线[x2a2-y2b2=1][a>0，b>0]上的动点，点[A，B]关于原点对称，且点[M]不与点[A，B]重合，直线[MA，MB]的斜率分别是非零的[k1，k2]，那么[k1k2]为定值，且[k1k2=b2a2].

（4）感悟.

借助GeoGebra软件，教师引导学生经历了探寻规律、发现规律、证实规律、推广规律的整个流程，让学生亲身体验并感悟到真理与结论的探索与发现路径，这有助于激发学生强烈的探索欲和求知欲，便于帮助学生树立正确的问题意识和创新意识. 同时，在探究实验的整个过程中，充分借用了GeoGebra软件进行直观展现，结合动手参与和独立思考，学生的数形结合能力得到了有效锻炼和提升，学生的直观想象素养得到了有效培育.

三、结语

GeoGebra软件能把几何图形由枯燥、生涩和冰冷变得动感、富有生命力和便于理解. 合理利用GeoGebra软件，可以为学生创造一个“数”与“形”完美融合的、易于接受和理解的学习空间，使学生的几何感知、空间想象能力的提升更有着力点，让学生的直观想象素养能更快、更有效地发育、成长和开花结果.

參考文献：

［1］浦丽俐. 新课标下高中生数学直观想象核心素养提升的实践研究［J］. 中学数学，2021（13）：96-97.

［2］纪晓平. 高中数学教学中直观想象的理解与教学［J］. 数学教学通讯，2021（18）：50-51.

［3］项俊. GeoGebra软件在高中数学教学中的应用探究［J］. 上海中学数学，2019（4）：25-27.

［4］张志勇. 高中数学可视化教学：原则、途径与策略：基于GeoGebra软件平台［J］. 数学通报，2018，57（7）：21-24，28.