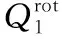伪双曲方程一个非协调混合元方法超收敛分析

马 戈, 胡双年

(南阳理工学院 数学与统计学院, 河南 南阳 473004)

0 引言

考虑如下伪双曲方程[1]:

(1)

其中X=(x,y),Ω为边界并行于坐标轴的有界矩形区域,其边界是∂Ω,f∈L2(Ω)、u0(X)、u1(X)为已知光滑函数，a(X)和b(X)为已知光滑函数，且满足a0≤a(X)≤a1，b0≤b(X)≤b1，这里a0,a1,b0,b1是正常数.

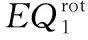
1 单元构造及问题逼近

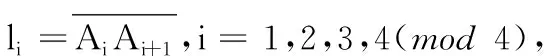
Vh={vh;vh|K∈span{1,x,y,x2,y2},

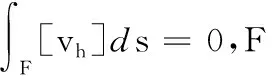
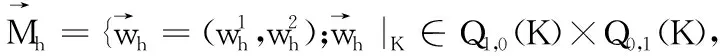
其中:Qm,n(K)=span{xiyj,0≤i≤m,0≤j≤n}，F是单元K的边，[vh]表示v跨过边界F的跃度，当F⊂∂Ω时，[v]=v.

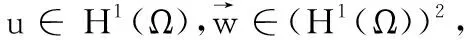
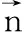
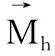
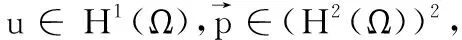
(2)

(3)

(4)

(5)

其中

显然‖·‖h是Vh上的模.

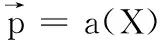
(6)

(7)

(8)

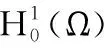
2 半离散格式下的超逼近分析

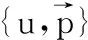
(9)

(10)

其中

证明记

(11)

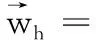
(ξtt,ξt)+(a(X)ξ,ξt)h+

(a(X)ξt,ξt)h+(b(X)ξt,ξt)=

-(ηtt,ξt)-(a(X)η,ξt)h-

(a(X)ηt,ξt)h-(b(X)ηt,ξt)+

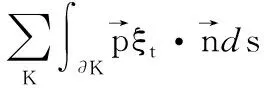
(12)

注意到式(12)的左端项

(ξtt,ξt)+(a(X)ξ,ξt)h+

(a(X)ξt,ξt)h+(b(X)ξt,ξt)≥

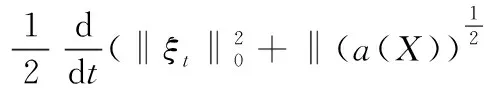
(13)

下面对式(12)的右端各项进行估计.应用性质1,平均值技巧及ε-Young不等式有

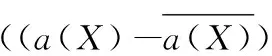
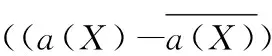
将上述对Bi(i=1,2,…,5)的估计及式(13)代入式(12)得

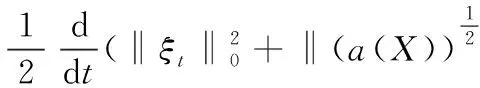
(14)

对式(14)两端从0到t积分，注意到ξt(X，0)=ξ(X，0)=0，并取ε充分小得

(15)

即式(9)得证.

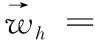
(ξtt,ξtt)+(a(X)ξt,ξtt)h+(b(X)ξt,ξtt)=

-(ηtt,ξtt)-(a(X)η,ξtt)h-

(a(X)ηt,ξtt)h-(b(X)ηt,ξtt)-

(a(X)ξ,=∶

(16)

下面估计式(16)右端各项.利用导数转移技巧、平均值技巧和引理1及ε-Young不等式有

D1+D4≤C(‖ηtt‖0+‖ηt‖0)‖ξtt‖0≤

D2=(a(X)ηt,η,ξt)h=

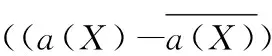
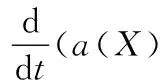
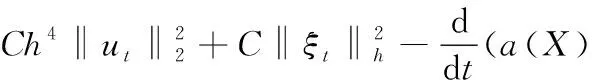
类似有

D3=(a(X)ηtt,ηt,ξt)h≤

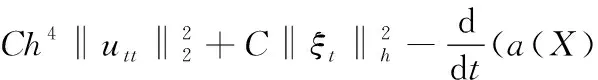
D5=(a(X)ξt,ξ,ξt)h≤

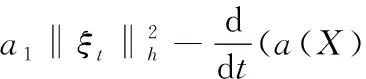
将上述Di(i=1,2,…,6)的估计代入式(16)有

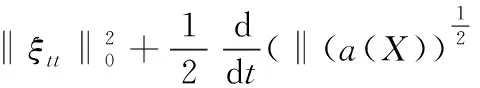
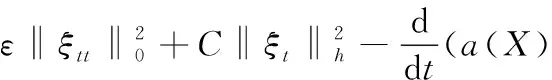
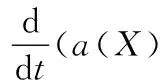
(17)

取ε充分小，对式(17)两端从0到t积分，并注意到ξt(X，0)=0，ξt(X，0)=0，可得

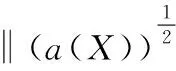
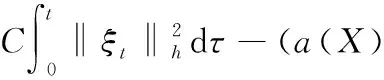
(a(X)η,ξt)h-

(a(X)ηt,

(18)

注意到a(X)≥a0>0，b(X)≥b0>0，由式(18)及Gronwall引理有

(19)

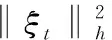
(a(X)(ξt+h≤

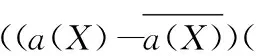
(20)

取ε充分小即得(10)式,定理得证.证毕.

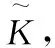
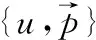
(21)

(22)

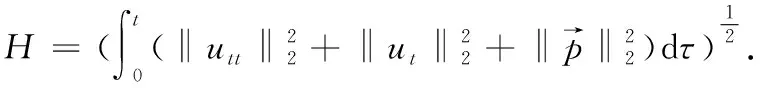
3 全离散格式下的超逼近分析

设0=t0

(23)

其中

(24)

其中

utt(X,0)=-b(X)u1(X)+(a(X)u1(X)+

a(X)u0(X))+f(X,0).

(25)

(26)

其中

证明记

(27)

(∂ttξn,∂tξn)+(b(X)∂tξn,∂tξn)+

(a(X)∂tξn)h+(a(X)ξtn,∂tξn)h=

-(∂ttηn,∂tξn)-(b(X)∂tηn,∂tξn)-

(a(X)∂tηn,∂tξn)h-(a(X)∂tξn)h+

(28)

注意到，方程(28)的左端

(∂ttξn,∂tξn)+(b(X)∂tξn,∂tξn)+

(a(X)∂tξn)h+(a(X)ξtn,∂tξn)h≥

(29)

下面对式(28)右端各项估计，注意有

则由引理1、Schwarz和ε-Young不等式

将上述Ei(i=1,2,…,6)的估计及式(29)，代入式(28)并取ε比较小有

(30)

对式(30)两端同乘以2τ，并对n从1到N-1求和，注意(N-1)τ≤T，得

(31)

应用Taylor’s展开易知

注意到

故有

(32)

将式(32)代入式(31)，并注意a0≤a(X)≤b0，可得

(33)

由于

(34)

(35)

综合式(33)、(34)和式(35)可得

(36)

即式(25)得证.

(a(X)

(37)

由引理1、Schwarz和ε-Young不等式，并应用式(36)的结论有

当网格比τ=O(h)，利用逆估计有

G3≤C‖

G6=(

将上述Gi(i=1,2,…,6)代入式(37)，并取ε充分小，有

(38)

再利用三角不等式可得式(26).证毕.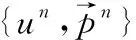

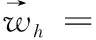
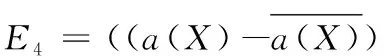
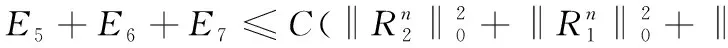
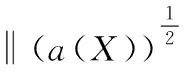
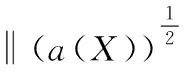
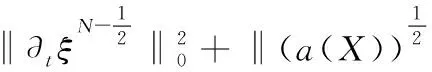
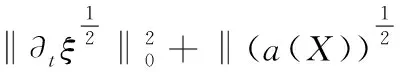
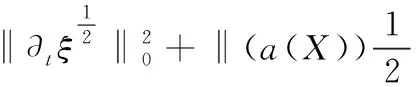
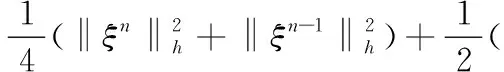
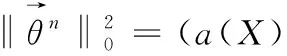
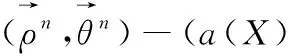
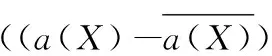
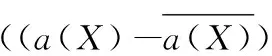
4 结语