赋权Myerson值与一致性

单而芳, 聂珊姗, 吕文蓉

(1.上海大学 管理学院,上海 200444; 2.上海大学 数学系,上海 200444)

0 引言

在效用可转移合作对策中,任何参与者之间都能形成可行联盟进行合作,并从中获得合作收益。合理分配参与者间产生的合作收益是保持其稳定合作的关键。SHAPLEY[1]根据参与者对不同联盟的边际贡献提出了著名的Shapley值。考虑到在现实中,一些参与者之间不能形成可行联盟,MYERSON[2]引入图以描述参与者间的合作通讯结构,将Shapley值推广到具有图结构的合作对策(简称图对策)上,提出了Myerson值并给出了公理化刻画。关于Myerson值最近的其他研究进展可参看LI和SHAN[3-6]、SHAN等[7]。

不过,在实际中不同参与者的讨价还价能力可能不同,为此可以根据每个参与者的实力,对其进行赋权以体现参与者的讨价还价能力。HAERINGER[8]基于SHAPLEY[9]提出的赋权Shapley值,将Myerson值推广到赋权图对策中,提出了赋权Myerson值,并证明它可以由分支有效性和赋权公平性所唯一确定。SLIKKER和VAN DEN NOUWELAND[10]把具有不同权值的参与者看作不对称参与者,利用分支有效性、类赋权公平性(class weighted fairness)、高阶独立性(independence of higher classes)和类一致性(class consistency)给出了赋权Myerson值的刻画。最近,WANG和SHAN[11]进一步讨论了赋权Myerson值的分解性质。

一致性公理最早由HART和MAS-COLELL[12]在1989年提出,并被用来刻画Shapley值。此后,该性质被广泛应用于值的公理化刻画中。WINTER[13]将一致性应用于到具有联盟结构的对策中,用一致性和其他四个性质刻画了著名的Owen值。DRANGAN[14]受HART和MAS-COLELL[12]研究的启发,构造了Banzhaf值的缩减对策,并据此提出了与该缩减对策相对应的一致性公理,用一致性和标准性给出了Banzhaf值的刻画。ALBIZURI和ZARZUELO[15]则将一致性推广到超图对策上,提出了对应于图对策的CS-一致性公理,并仿照Shapley值的潜能函数[12]定义了Myerson值的潜能函数,然后借助潜能函数,用CS-一致性和CS-标准性刻画了超图对策上的Myerson值。

本文的目的是用一致性公理来刻画赋权Myerson值。一般地,利用一致性公理来刻画对策的值时,需要借助潜能函数做工具才能完成值满足一致性的证明。本文在提出赋权图对策上的缩减对策和缩减图后,避开潜能函数的概念,直接建立了在赋权Myerson值下每个联盟在缩减图限制对策和原图限制对策下红利之间的关系式,由此证明了赋权Myerson值满足一致性,并最终利用权意义下的一致性和标准性给出了赋权Myerson值的刻画。

下一节介绍本文所涉及的概念、记号和术语。第三节首先提出赋权图对策中的缩减对策、缩减图概念和一致性公理,其次建立联盟在赋权缩减图限制对策和原赋权图限制对策下红利之间的关系式,然后利用权意义下的一致性和标准性给出赋权Myerson的公理化刻画。最后一节对本文进行了总结。

1 预备知识

1.1 TU-对策和Shapley值

效用可转移合作对策,简称TU-对策,由二元组(N,v)构成,其中N={1,2,…,n}表示参与者(player)的集合,通常称为N大联盟,v表示特征函数(characteristic function),它是定义在N的幂集2N上的一个实映射,并且规定v(φ)=0。N的任意子集S称为联盟,v(S)表示联盟中的参与者进行合作所产生的效用(worth),用|S|或s表示联盟的基数。将N上所有TU-对策的集合记作GN。以下提到的对策均指TU-对策。

对于S∈2N{φ},对应于S的一致性对策(N,uS)[1]定义为:若S⊆T,则uS(T)=1,否则uS(T)=0。任意TU-对策(N,v)都可以用一致性对策唯一线性表示[16],即

(1)

其中ΔS(v)为联盟S的Harsanyi红利,其表达式为

(2)

在TU-对策(N,v)中,x=(x1,…,xn)∈Rn表示一个支付向量,其中xi表示第i个参与者所获得的支付。分配规则φ是定义在GN上的一个函数,也即φ:GN→Rn,φi(N,v)表示给参与者i∈N的支付。

在TU-对策中,最著名的分配规则是Shapley值[1],其红利表达式为

参与者i的Shapley值等于包含它的每个联盟红利的均值之和。

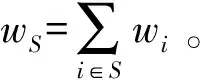
(3)

在合作对策理论中,Shapley值已被广泛应用于许多领域,对社会、政治、经济和科学等领域的发展均产生了深刻影响。此外,根据不同的实际背景,它已被推广到诸如优先联盟合作结构、通讯图合作结构等不同的合作结构环境中。

1.2 图对策和赋权Myerson值

1977年,MYERSON把Shapley值推广到具有通讯图结构的合作对策中,提出了著名的Myerson值[2]。下面介绍相关的概念。

一个图由二元组(N,L)表示,其中N是顶点的集合,每个顶点代表一个参与者,L⊆LN={{i,j}|i,j∈N,i≠j}是边的集合,代表参与者之间的通讯联系。为方便起见,本文用ij代替{i,j}来表示边。如果ij∈L,称i和j在图中是直接连通的。对于不直接相连的参与者i和j,也可能通过其他参与者作为“中介”实现连通。如果存在一条路(path),也就是参与者序列(i1,i2,…,it),i1=i,it=j,使得对于所有k∈{1,2,…,t-1}有{ik,ik+1}∈L,则称i和j是连通的。这条路也称为i-j路,路的长度定义为该条路上边的个数。若图中任意两点均是直接连通或连通的,则称这个图是连通的。在图(N,L)中,每个极大的连通子图称作一个分支,用N/L表示图(N,L)所有分支的集合。对任意S⊆N,由联盟S导出的子图记作(S,LS),其中LS={ij|ij∈L,i,j∈S},用S/LS表示S所有分支的集合。如果(S,LS)是连通的,则联盟S是连通的。

一个图对策由三元组(N,v,L)所构成,其中(N,v)是一个TU-对策,而(N,L)是一个图,用CSN表示N上所有图对策的集合。MYERSON假定每个连通联盟才是可行联盟,并在此假设下引入了图限制对策(N,vL)[2],其中特征函数vL定义为

(4)

MYERSON把图限制对策(N,vL)的Shapley值作为一个分配规则,这就是著名的Myerson值[2],其表达式为μi(N,v,L)=Shi(N,vL)。

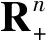
(5)

像引言中提到的,HAERINGER证明了赋权Myerson值可以由分支有效性和权公平性所唯一确定。而SLIKKER和VAN DEN NOUWELAND利用分支有效性、类赋权公平性、高阶独立性和类一致性给出了赋权Myerson值的不同刻画。

2 一致性与公理化刻画

2.1 一致性

一致性公理在值的公理化刻画中具有重要的作用,为完成赋权Myerson值的公理化刻画,我们首先引入赋权缩减图对策和缩减图的定义。

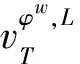
(6)

这里的Tc=NT表示T的补集,也即不在联盟T中的参与者,而w|S∪Tc表示权向量w在S∪Tc上的限制。赋权缩减图对策的含义为:在赋权缩减图对策下,联盟S的效用等于联盟S与所有离开的参与者在赋权图限制对策下进行合作所产生的效用,减去所有离开的参与者按照原分配规则φw所分得的收益和。

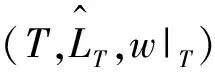
(7)

这里N(P)表示路P上参与者的集合。赋权缩减图的边包含两部分,一是由T导出的子图的边,也即LT。二是新增加的边:若T中的两个参与者能由T之外的参与者形成的路所连结(除T中的这两个参与者外,路上的其他参与者均在Tc中),则在这两个参与者之间增加一条边。

在定义了赋权缩减图对策和缩减图的基础上,现提出权意义下的一致性公理。

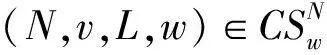
则φw称具有w-一致性。

2.2 赋权Myerson值的公理化刻画

为了证明赋权Myerson值满足w-一致性,根据上一小节所定义的赋权缩减图对策和缩减图,本小节首先给出一个关键的引理。这个引理给出了在赋权Myerson下任意联盟S⊆T在赋权缩减图限制对策和原赋权图限制对策中的红利关系式。

引理1设(N,v,L,w)为任意的赋权图对策,T⊆N,则对任意的S⊆T,S在赋权缩减图限制对策的红利值满足

下面利用上述引理证明赋权Myerson值满足w-一致性。

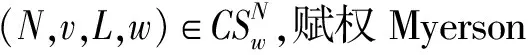
为最终给出赋权Myerson值的公理化刻画,我们需要引入下面的w-标准性。

w-标准性的含义为:对于一个两人赋权图对策,若两个参与者不连通,则每个参与者所获得的收益为自身产生的效用。若两个参与者连通,则每个参与者先获得自身产生的效用,再将剩余效用按照自身权重与总权重的比例进行分配。容易证明赋权Myerson值满足w-标准性。

在利用w-一致性和w-标准性给出赋权Myerson值的刻画之前,我们首先证明,若分配规则满足w-一致性和w-标准性,则其一定满足分支有效性。

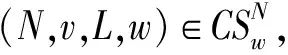
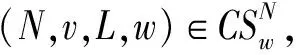
3 结论

本文研究了赋权图对策中赋权Myerson值的公理化刻画问题,用一致性公理给出了赋权Myerson值的新的刻画。为达到此目的,提出了赋权缩减图对策和缩减图的定义及赋权意义下的一致性公理。通过建立每个联盟在赋权缩减图限制对策和原赋权图限制对策中的红利关系,证明了赋权Myerson值满足一致性,从而避开以往文献中需要借助潜能函数才能完成的满足一致性证明。最后用w-一致性和w-标准性给出了赋权Myerson值的公理化刻画。