考虑数据异质性的海上通道事故严重程度研究

李宝德, 吕 靖, 李 晶

(大连海事大学 交通运输工程学院,辽宁 大连 116026)

0 引言

海上事故指的是一种不希望发生的船舶异常事件,经常导致人员伤亡、船舶损伤或者各种财产损失[1]。尽管国际海事部门已经为运输安全做出了巨大的努力,但是海上运输通道发生事故的风险依然存在。因此,探究影响海上通道事故严重程度的因素,对于及时有效的应急响应,降低事故造成的损失具有重要意义。

海上事故发生后的演变是一个复杂的过程,受到众多因素的影响。目前许多学者从不同视角探究了海上事故严重程度的影响因素。比如,WENG和YANG[2]研究发现在恶劣天气和黑暗条件下发生的碰撞、火灾/爆炸、接触等事故其发生致命事故的概率和死亡人数都较高。WANG和YANG[3]以事故预防为视角,开发了基于贝叶斯网络的事故严重程度评估模型,得出事故类型、位置、船舶类型等影响航道事故严重程度的关键风险。EROL等[4]对伊斯坦布尔海峡发生的事故研究发现,无论船舶大小,当海峡天气状况不佳时,事故严重程度会增加。陈兴伟等[5]采用结构方程模型探究了影响因素与事故严重程度之间的关系,结果表明客观因素与事故等级之间存在明显的影响方向性。总结之前研究可以发现,大多数是基于获得的数据以自身研究的角度直接分析因素对事故严重程度的影响,对于影响因素对事故严重程度的交互影响及可能存在的干扰因素的影响的考虑相对缺乏。

然而,考虑到海上事故可能发生在不同的条件下,这导致事故动力学本质的异质性,以及某些特定因素对事故后果的影响程度不同甚至方向相反。比如,WENG和YANG[2]研究认为船舶类型不能充分解释对事故后果严重程度的影响,而WANG和YANG[3]研究发现船舶类型对事故后果严重程度影响显著,特别是渔船。因此,一些研究为了减少异质性的影响,关注某一特定特征情况下的研究。比如,WENG[6]等研究影响两船碰撞严重程度的因素,得出春季、能见度低和夜间是导致船舶碰撞严重程度高的重要因素。ANTAO和SOARES[7]采用贝叶斯网络评估了不同天气条件下船舶事故中的人为失误因素。然而,基于具体特征的分析不能保证所选事故数据的最大同质性,因此,它对降低未观测的异质性作用不大。

聚类分析已经被证实可以用来识别同质类别和降低数据的异质性[8]。特别地,对于多分类问题,与潜在类别聚类相结合的多项logit模型比将单个多项logit模型综合应用于整个数据更有效[9]。目前,基于聚类的logit模型在交通事故领域有着丰富的应用[10]。然而,此种方法在海上通道事故分析中却很少。另外,先前采用聚类的logit模型很少考虑每个聚类类别内的异质性,而混合logit模型能够通过考虑影响因素的潜在变化来解决未观察到的聚类类别内的异质性[9]。

本文在现有研究的基础上,充分考虑海上事故数据的异质性,旨在构建一种结合潜在类别聚类和混合logit模型的两步模型来分析影响海上事故严重程度的因素。基于从中国海事局发布的事故调查报告中提取的数据验证模型的有效性。通过估计的参数和相关的边际效应结合起来解释所建立模型的重要变量。此外,通过采用聚类和没有采用聚类(全数据)的混合logit模型估计的结果对比,来揭示其中隐藏的影响变量。

1 模型构建

如图1所示,构建的两步模型包括潜在类别聚类和混合logit模型。潜在类别聚类是一种概率模型,它假设整个数据被一个未观察到的或潜在的分类变量划分为排他性的潜在类别[11]。为了更好地捕获因素对海上事故严重程度影响的未观察到的异质性。本研究第一步采用潜在类别聚类进行分析,但是每个聚类类别内仍可能存在异质性,因此,本研究第二步采用混合logit模型来分析第一步获得的每一个聚类。具体每一步的模型构建如下:

图1 海上通道事故严重程度分析两步模型

1.1 海上通道事故严重程度潜在类别聚类分析模型构建

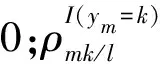
(1)

其中,采用期望最大化算法对参数进行极大似然估计。另外,基于贝叶斯定理,一个事故的后验概率可以表述为:

(2)

在潜在类别聚类分析中,类别nc的最合适数量是未知的,通过尝试不同聚类数量的模型,我们可以找到最合适的聚类数量。根据事故的特征,我们可以计算它们的最大后验概率,然后将它们分配到一个潜在的类别。在这个过程中,选择聚类的数量是为了最小化分配误差,可以通过一些信息准则来测量模型的分配精度,包括BIC,AIC,CAIC。BIC,AIC和CAIC的统计可以在考虑复杂性的同时衡量模型的适用性,BIC,AIC,CAIC值低对应的聚类数量具有较高价值,然而当分析大样本时,增加聚类的数量可能并不总是达到最小值,因此有的研究建议使用不同模型之间的BIC的百分比减少来衡量[5]。熵(Entropy)度量本质上是个体后验概率的加权平均值,范围在0和1之间,熵度量值越大,表明潜在的聚类分离越好。本研究使用AIC,BIC,CAIC和熵来识别合适的聚类数量。

1.2 基于聚类的混合logit模型构建

海上事故发生后可能造成的后果的严重程度可以采用不同的等级来进行衡量。因此,可以将基于潜在类别分析获得的不同的同质类别,分别构建影响因素与严重程度之间相关关系的离散选择模型。具体地,描述事故严重程度的效用函数可以表示如下[12]:

Sij=βjXij+εij

(3)

式中,Sij表示事i故为严重程度j时的效用函数;Xij为事故严重程度影响因素集;βj为影响事故严重程度因素的参数向量;εij为误差项。当εij服从广义极值分布型I(Gumbel type1)时,则事故i为严重程度j时的概率可表示为:

(4)

式中,J为事故严重程度等级集合。相比于多项logit模型,混合logit模型认为βj不是固定不变的,而是符合一定分布的随机向量。则概率密度函数可表示为:

(5)

式中,f(β|φ)为随机参数β向量的概率密度函数;φ为概率密度函数的参数向量。关于混合logit模型的参数估计,本文可以采用极大似然估计法。

此外,本研究还对获得的模型进行边际效应分析和拟合优度检验。边际效应分析的目的是为了评估混合logit模型中重要变量对事故严重程度概率的影响。对于连续变量来说,边际效应表示结果的概率相对于该变量单位变化的改变值,而二元变量的边际效应表示自变量从编码虚变量0到1的概率变化。这两种类型变量的边际效应可以分别用如下公式(6)和(7)表示[13]:

(6)

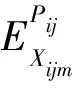
(7)

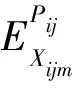
(8)

式中,LL(β)和LL(0)分别为收敛时和仅包含截距项的对数似然函数值。ρ2的值越大说明模型拟合的效果越好。对于模型之间的拟合优度比较,可以采用似然比与一定置信水平和自由度的卡方临界值进行比较来分析。似然比计算公式为:

(9)

式中,LL(βaggregate)在本研究为全数据模型收敛时的对数似然函数值。在本研究为LL(βclusterl)为第l个聚类模型收敛时的对数似然函数值。

2 实证研究

2.1 数据收集及预处理

本文研究的数据来源于中国海事局官网发布的海上事故调查报告。我们从中筛选了在2014年到2020年间的发生在海上运输通道上的765份用于分析。

关于事故严重程度,根据我国《水上交通事故统计办法》,按照人员伤亡情况、直接经济损失或者水域环境污染情况将事故分为小事故、一般事故、较大事故,重大事故和特别重大事故。根据我们的统计时间段,特别重大事故没有发生。因此,为了便于研究,本文将重大事故和特别重大事故定义为非常严重事故(VS)、较大事故定义为严重事故(S)、一般事故定义为轻微严重事故(LS)、小事故定义为海上事件(MI),具体事故严重程度的划分请参阅《水上交通事故统计办法》。

关于影响因素的选取及分类,主要参考了之前的相关研究[2,3,14]。对于其中的缺失值,采用均值法进行了补充,具体结果见表1。其中需要说明的是航行环境指的是航行地理环境,船舶流指的是事故发生时周围船舶数量;事故类型的分类是依据《水上交通事故统计办法》,将其划分为7类;船舶类型的分类是参考了欧洲海事安全局发布的事故统计报告中对船舶类型的划分标准。

2.2 结果及讨论

2.2.1 潜在类别聚类结果及讨论

使用表1所有的影响事故严重程度变量,对不同聚类数(1-8)的模型进行了初步估计,结果如图2所示。三种信息准则值随着聚类数的增加而降低。然而,从第四个聚类开始,BIC,AIC和CAIC的信息准则值下降百分比不到1%,说明四个聚类能够良好的分离数据。此外,四个聚类对应的熵值为0.966,表明模型具有良好的适应性。因此,海上事故数据分为四个聚类类别以供进一步分析。

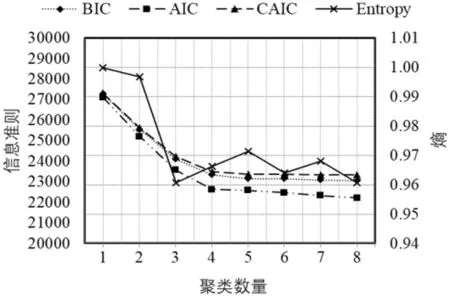
图2 不同聚类数下的AIC,BIC,CAIC和熵值

表1 关键影响变量选取及分类

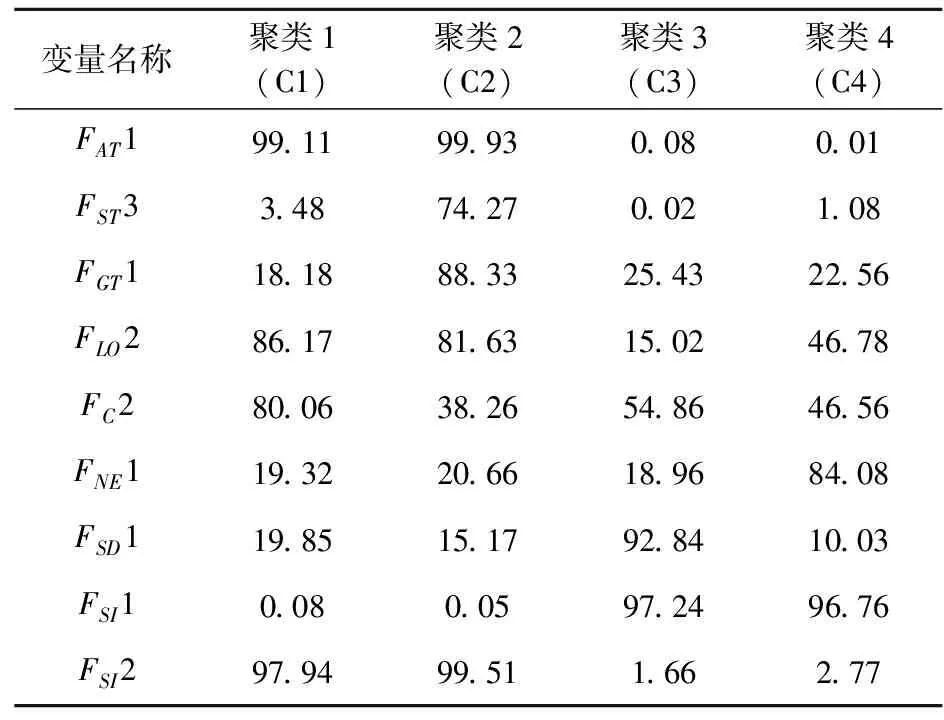
表2 聚类中关键特征变量及分布(%)

表2展示了用于描述每个聚类选定的特征变量及其分布情况。从中可以看出,每个特定的聚类中都有明显不同其他聚类占比的变量,需要注意的是有些变量占比可能会在不同聚类之间都很高。例如,在聚类1和聚类2中,发生的事故类型主要为碰撞,占比达99%以上,而其他聚类在相同条件下碰撞事故占比不到10%,因此,变量“事故类型:碰撞”可以将聚类1和聚类2与其他聚类区分开来。另外,变量“船员:配备足够船员且有有效的适任证书”在聚类1中占比最高并且与在其他聚类中占比相比相差很大,说明这个变量可以将聚类1与其他聚类区别开来。同样的,每个聚类可以通过自己特有的影响变量分布情况将其与其他聚类分离开来,代表了一种特定情况下的具体事故类型。需要说明的用于描述每个聚类的影响因素与影响事故严重程度的重要因素之间没有关系,将在接下来混合logit模型中揭示影响事故严重程度的重要因素。

表3 轻微严重事故模型参数估计结果

2.2.2 混合logit估计结果及讨论

对于通过聚类获得的四个聚类类别及全数据分别进行了建模分析。采用逐步向前回归技术对构建的混合logit模型进行标定,在95%置信水平下,每个模型获得的显著影响变量参数估计的结果见表3-表5(其中,表中“-”表示该置信水平下不显著)。对于事故严重程度,本文选择海上事件作为参考项;而对于影响变量,本文以表1分类描述的最后一项作为参考项。研究发现,在聚类1,2,3和4中,影响变量对海上事故严重程度具有统计上显著的随机影响。结合估计出的显著变量,为进一步分析各个因素对海上事故严重程度的影响,对所有重要变量的边际效应进行了计算,具体获得的边际效应值见表6-表10。

表4 严重事故模型参数估计结果

首先根据估计的结果,可以发现一些重要的影响事故严重程度的因素。比如事故类型为自沉,相比于其他事故类型,对事故严重程度为轻微严重、严重和非常严重都具有显著影响,说明这个变量是对事故严重程度的影响一个非常重要变量,这个与汪飞翔等[14]的研究结果相一致。此外,与WANG和YANG[3]研究得出的结论相同,差的航行环境、事故发生在夜晚(见表3-表5)也会对事故严重程度产生重要的影响。另外,本文研究发现船舶流少相对于流多会增加严重事故的程度(见表4聚类4),可能原因是事故发生后,如果周围参与救援的力量越多,越可能降低事故严重程度。另外,通过估计模型间的比较分析,可以得出如下发现:

表5 非常严重事故模型参数估计结果

第一,可以发现基于异构数据的海上事故分析可能会掩盖一些重要的影响因素。例如,表4中的变量液体货船、船龄6-10年和11-15年、装载情况正常、风5-7级、航行环境差以及船舶流量少在全数据模型中没有统计学意义。然而,根据聚类中的模型这些变量会对轻微严重程度事故产生不同程度的影响。同样情况在严重事故以及非常严重事故的模型参数估计中也存在(见表4和5)。

第二,基于聚类的模型能够揭示影响变量 对不同特定情况下的事故严重程度概率的变化。例如,发生的事故船舶类型为渔船,根据全数据模型造成轻微严重事故的概率将增加3.5%(见表6),而根据聚类1、聚类2和聚类4模型造成轻微严重事故的概率分别增加11.3%(见表7)、12.6%(见表8)和5.7%(见表10)。此外,相比于船龄大于等于20年,发生的事故船舶船龄在11-15年,根据聚类1模型造成严重事故的概率将下降6.2%(见表7),而根据聚类4模型造成严重事故的概率将下降13.8%(见表10)。以上两个例子说明了仅仅通过全数据模型会忽视这种差异,而基于聚类的模型能够更加完整的揭示这种差异。

表6 全数据模型显著变量平均边际效应

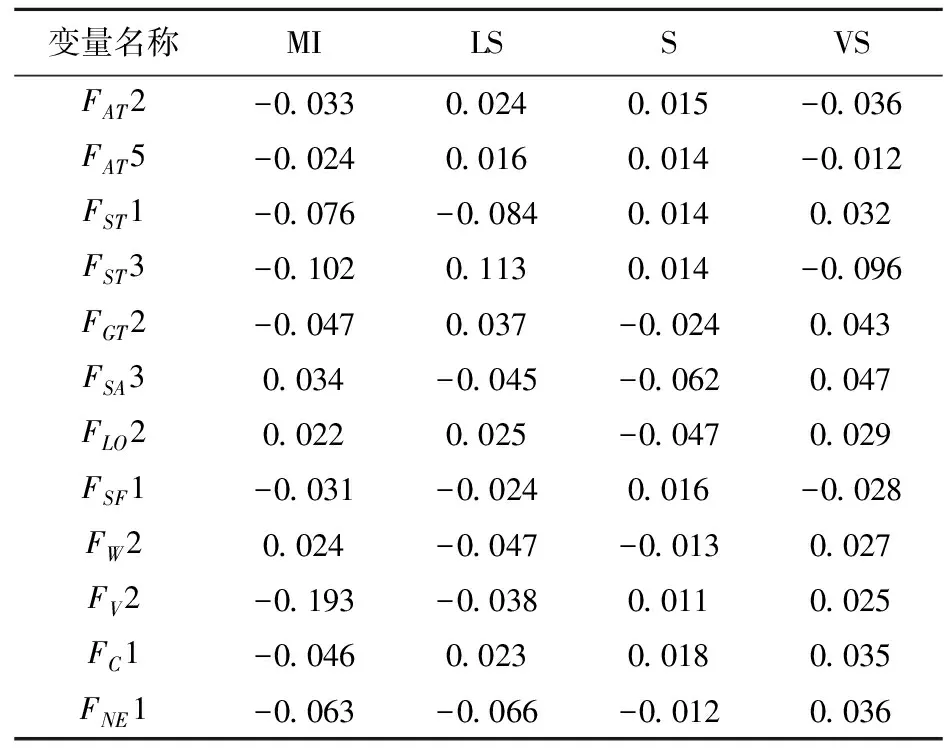
表7 C1模型显著变量平均边际效应

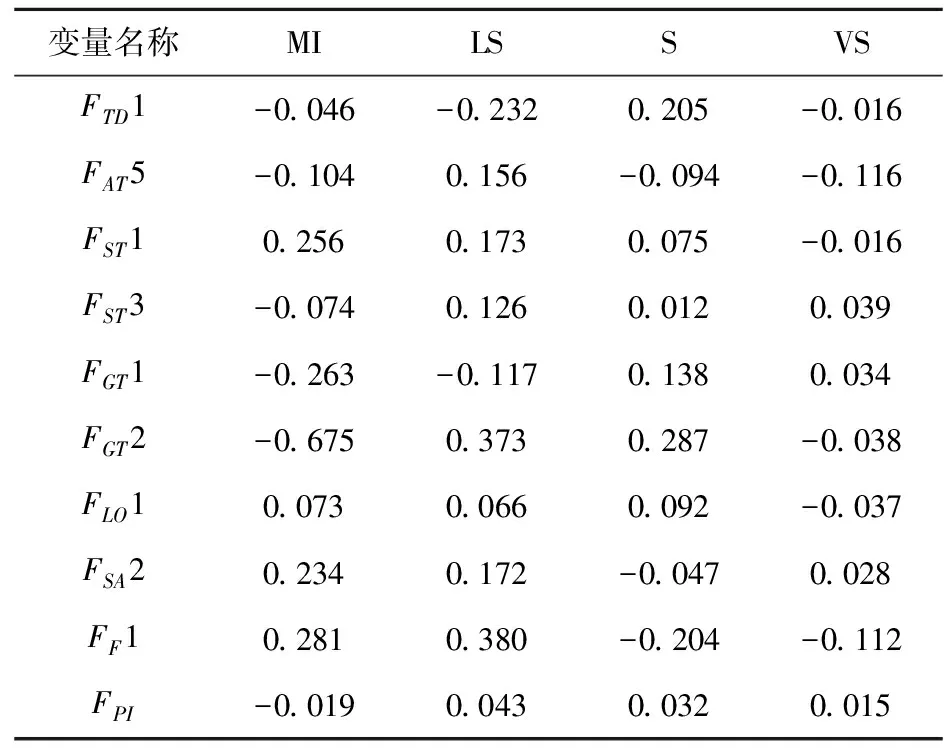
表8 C2模型显著变量平均边际效应

表9 C3模型显著变量平均边际效应

表10 C4模型显著变量平均边际效应

第三,聚类模型甚至可以揭示某些变量对事故严重程度影响方向的不同。例如,在表4的聚类3模型中显示船舶流少会降低事故严重程度,而在聚类4模型中显示相反的结果。具体地,结合表9和10,在聚类3模型中事故发生时周围船舶流少将会使严重事故的概率降低9.3%,在聚类4模型中会使概率增加5.7%.

2.2.3 模型的拟合优度结果

表11展示了计算获得的用于测量每个模型拟合优度的参数,得到的似然比值为102.03大于95%置信水平下自由度为29的卡方值(42.56)。说明了基于聚类的模型优于全数据模型。另外从ρ2值可以看出每个模型都有很好的拟合性。

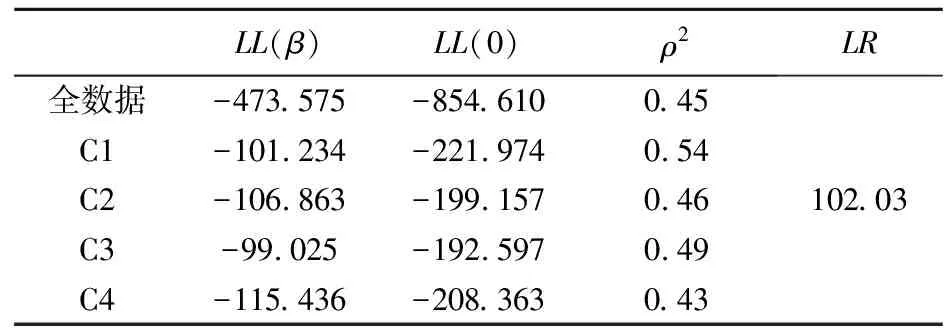
表11 拟合优度测量参数

3 结论

本文充分考虑到海上事故数据的未观测到的异质性,构建了结合潜在类别聚类和混合logit的海上事故严重程度分析模型。研究表明了基于聚类的混合logit模型可以更加有效的揭示影响因素与事故严重程度的关系。通过比较分析获得如下结论:(1)基于聚类的模型可以揭示新的信息,包括在全数据模型中被忽略的重要影响因素以及在基于聚类模型中具有不同影响程度的因素;(2)基于聚类的模型可以揭示不同聚类类别下影响因素对海上事故严重程度的影响的差异。本文依靠从海上事故报告中搜集的信息,获得的数据有限。因此,在未来研究中,随着数据的不断完善可以进行更加完整的分析。