基于重要度的风力发电系统可靠性优化分析

2023-02-22兑红炎张雨露张云安

运筹与管理 2023年12期

兑红炎, 张雨露, 刘朝, 张云安

(1.郑州大学管理学院,河南郑州 450001; 2.国防科技大学智能科学学院,湖南长沙 410073)

0 引言

面对中国电网出台的能源转型政策和国务院颁布的双碳政策,能源和环境问题再次受到关注。风力发电是解决能源和环境问题最好的发电模式之一。2020年我国累计装机容量达262.10GW,超额完成了“十三五”规划的风电装机目标,风力发电在我国得到了广泛的关注与发展。随着风力发电机数量和装机容量的增加,风力发电系统规模加大且变得更加复杂化。节点影响风力发电系统可靠性,节点故障导致风力发电系统故障,造成人力、物力和财力的损失。因此,如何准确评估风力发电系统可靠性对整个电网至关重要。通过重要度理论评估节点对风力发电系统的影响程度和梯度理论对风力发电系统进行可靠性优化,可以帮助管理者识别和解决风力发电系统可靠性问题。

重要度理论是系统可靠性理论的分支,帮助管理人员对系统可靠性进行设计、运行和维护。自BIRNBAUM[1]首次提出可靠性重要度概念后,重要度理论在可靠性理论领域得到了广泛的拓展与更新,并在航空航天、交通、核能、配电网和无人机等领域得到了广泛的应用。GRIFFITH[2]提出了多状态下部件单级退化对系统可靠性影响的Griffith重要度。兑红炎等[3]提出了组件多状态退化对系统可靠性影响的综合重要度,对组件综合重要度变化机理进行分析。高雪莉和崔利荣[4]对重要度分析,提出其常用于各类系统的可靠性设计、故障诊断和优化等方面。兑红炎等[5]综合分析了三种重要度,给出了重要度在梯度中的表示与几何意义。张权等[6]研究了半马尔科夫下电场系统可靠性分析,利用马尔科夫更新知识给出可用度。崔利荣等[7]提出了基于二元维纳过程的系统可靠性和可用度分析,给出不同维修策略下的可修表达式。在风力发电系统可靠性与维修研究领域,兑红炎等[8]提出了风力发电系统弹性模型,研究了多节点故障后的恢复顺序。崔利荣等[9]以风力发电系统为例,提出了由复杂故障过程和购电协议影响的能源系统的可靠性维护。吴晨曦等[10]考虑先进绝热压缩空气储能系统,对风力发电系统成本进行可靠性评估。ZHU等[11]基于风力发电机实时状态评估风力发电系统可靠性并改进。ZHENG等[12]基于半马尔可夫决策过程,提出了考虑风速加速危险率、限制维修实施和影响停机时间的风机预防性维修策略。TUYET和CHOU[13]考虑系统可靠性、成本效益、天气条件等参数,提出动态维修和分组维修模型,确定海上风力发电系统最优维修计划。YANG等[14]考虑停机期间损失,集成风力条件和维修资源约束,提出风力发电场的维修策略。CHAN和MO[15]研究维修策略对风机全寿命周期成本的影响,并优化风机可靠性。

本文提出基于重要度的风力发电系统可靠性优化模型,分析风力发电系统中节点可靠性变化对系统可靠性的影响,基于风速与功率的关系研究风力发电系统可靠性。然后,基于Birnbaum重要度与综合重要度研究节点对风力发电系统的影响程度。最后,基于重要度梯度研究风力发电系统可靠性提升最快的方向。

1 风力发电系统可靠性

风力发电系统是一种将风能转化为电能的清洁型电网系统。为方便分析,规定每个风力发电机具有相同额定功率,剩余节点均为电力需求节点。图1为风力发电网络图,由电力供给节点(风力发电机)、电力需求节点与节点之间的输电边构成。

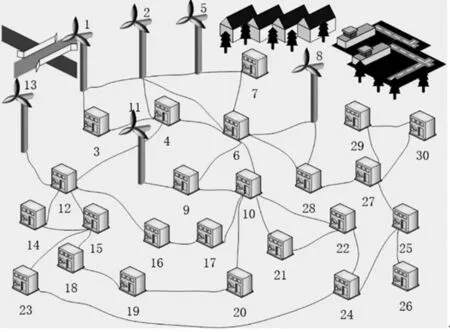
图1 风力发电网络图

一定的风速吹动扇叶使风力发电机产生输出功率Pn。当风速过高或过低时,导致风力发电机故障以及风力发电系统可靠性下降。因此,风力发电机输出功率与风速密切相关。可以用切入风速vin、额定风速vn和切出风速vout对风力发电机实际输出的额定功率进行描述。标准空气密度条件下,风力发电机的实际输出功率Pw与风速关系如图2所示。

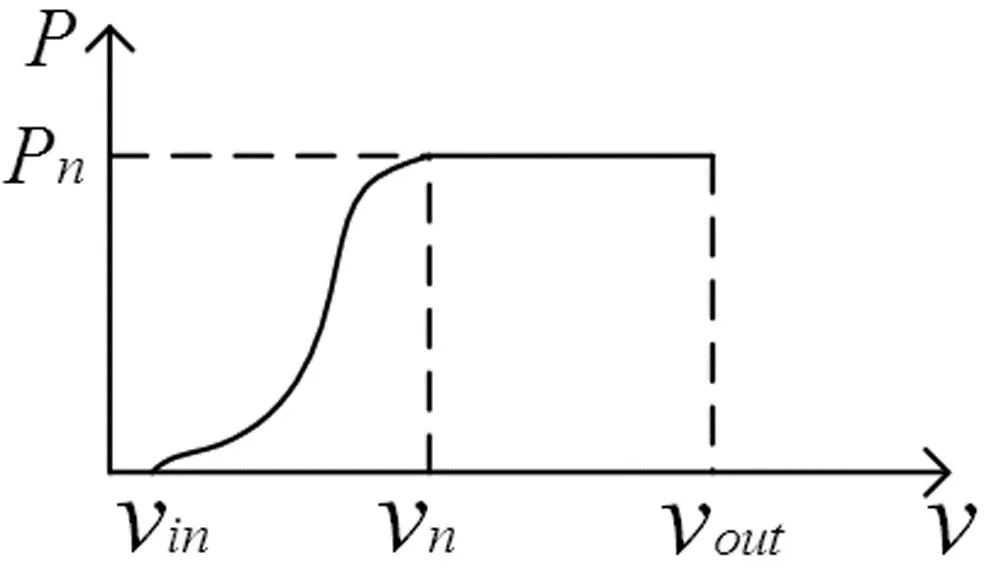
图2 风速与实际输出功率关系图

当风速小于切入风速或大于切出风速时,风力发电机会自动停机或出现塔架坍塌、叶轮飞车等事故。因此,这两种情况下风力发电机为故障状态且输出功率为0。风力发电机的实际输出功率与风速的关系式如下:

(1)

与一般系统可靠性不同,风力发电系统可靠性用供电履行水平而非寿命作为自变量来衡量。其中,供电履行水平取决于人均需求用电量和单位发电量。风力发电系统可靠性定义为在指定运行条件下,在规定时间内达到用户所需用电量的概率。

(2)

其中,t和d分别为用电需求时间和需求用电量;随机变量T和Q分别为发电时间和发电量。Q/T表示单位时间内的发电量,等价于实际输出功率Pw。d/t表示单位时间内的需求电量,用Pd表示。

R(Pd)=Pr{Pw≥Pd}

(3)

公式(3)中,R(Pd)表示风力发电系统可靠性。

风力发电串联系统中,风力发电系统由n个风力发电机串联而成,任意一个风力发电机输出功率小于切入风速或大于切出风速就会引起该设备故障,进而引起风力发电系统失效。假设第i个风力发电机的输出功率为Pwi,可靠度为Ri(Pd),i=1,2,…,n。

由串联可知,风力发电系统的发电量为:

Pw=min{Pw1,Pw2,…,Pwn}

(4)

风力发电系统可靠性为:

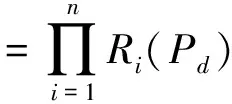
(5)

风力发电并联系统中,风力发电系统由n个风力发电机并联而成,所有风力发电机输出功率小于切入风速或大于切出风速时就会引起该设备故障,进而引起风力发电系统失效。假设第i个风力发电机的输出功率为Pwi,可靠度为Ri(Pd),i=1,2,…,n。

由并联可知,风力发电系统的发电量为:

Pw=max{Pw1,Pw2,…,Pwn}

(6)

风力发电系统可靠性为:

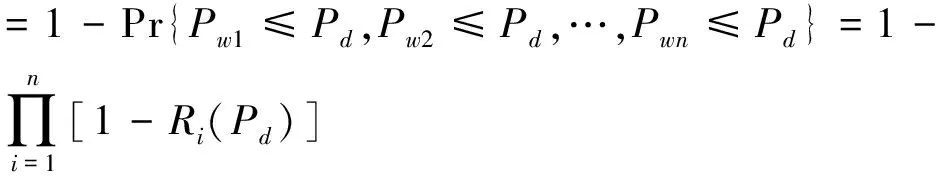
(7)

2 基于重要度梯度的风力发电系统可靠性分析

重要度是指当部件状态发生变化或故障时,对系统可靠性的影响程度。风力发电系统中,系统重要度是由节点重要度得到的。当节点状态发生变化或故障时,对风力发电系统可靠性产生影响。本节对风力发电系统进行基础建模,定义风力发电系统的Birnbaum重要度和综合重要度,通过重要度梯度研究风力发电系统可靠性增长最快的方向,分析固定资源下故障节点的维修顺序。

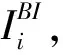
(8)

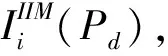
(9)

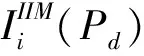
梯度是一个连续函数对所有变量偏导数组成的向量,梯度方向指向函数增长速率最大的方向。重要度是一个标量,它是系统可靠性函数对部件可靠性变量的偏导数。通过重要度在梯度中的表示,可以得出系统可靠性增长最大的方向。f表示连续函数f(x1,x2,…,xn)的梯度,表示xi方向上的单位正交向量。梯度一般表达式如下:

(10)

风力发电系统中,所有节点的Birnbaum重要度组成系统可靠性函数f(Pw1=1,Pw2=1,…,Pwn=1)的梯度。梯度表明了在点(Pw1=1,Pw2=1,…,Pwn=1)处风力发电系统可靠性提升最快的方向,梯度的大小决定了风力发电系统可靠性在该方向上上升的速度。节点的Birnbaum重要度在梯度中的表达式如下:

(11)

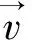
(12)

为了找出风力发电系统可靠性增长最快的方向,使系统可靠性得到优化,需要对不同节点的重要度进行排序及梯度计算。由于故障节点的位置、组成和特性不同,维修成本也不同。因此,本文选择一组故障节点在固定成本约束下进行维修,使风力发电系统的可靠性达到相对最优状态。具体如下:

(1)分析风力发电系统中各个节点的重要度并进行优先级排序,比较不同重要度下节点对风力系统可靠性的影响程度。

(2)根据不同节点故障后所需的维修成本不同,研究固定资源约束下维修故障节点的顺序,使系统可靠性最大化恢复。

(3)研究节点重要度的梯度,分析风力发电系统可靠性增长最快的方向。

3 案例仿真

将图1所示的某风力发电网络简化为如图3所示的风力发电逻辑网络图。逻辑网络中的节点代表发电节点和耗电节点,边代表节点之间的输电网络。将风力发电系统的逻辑网络表示为N(P,E),其中P为节点集,E为边缘集。P包含两个子集:供应节点子集PG和需求节点子集PD。供给节点子集PG包含节点G1、节点G2、节点G5、节点G8、节点G11以及节点G13。需求节点子集PD包含节点D3、节点D4、节点D6、节点D7、节点D9、节点D10、节点D12、节点D14以及节点D15至节点D30。

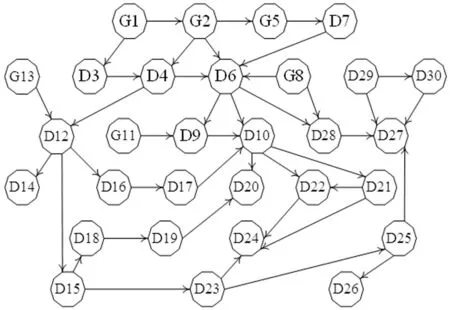
图3 风力发电逻辑网络图

假设节点之间互相独立,需求节点的可靠性服从指数分布,需求节点故障率为0.006/周。供给节点的可靠性由供需用电概率得到,供给节点的故障率分别为0.004/周、0.006/周、0.005/周、0.005/周、0.008/周、0.007/周。以2020年月用电量65度为基础,某地区人群单位时间内的需求用电量为20kW。风力发电机运行周期为60周,节点i的可靠性为Ri(Pd)。根据公式(3),节点可靠性如表1所示。

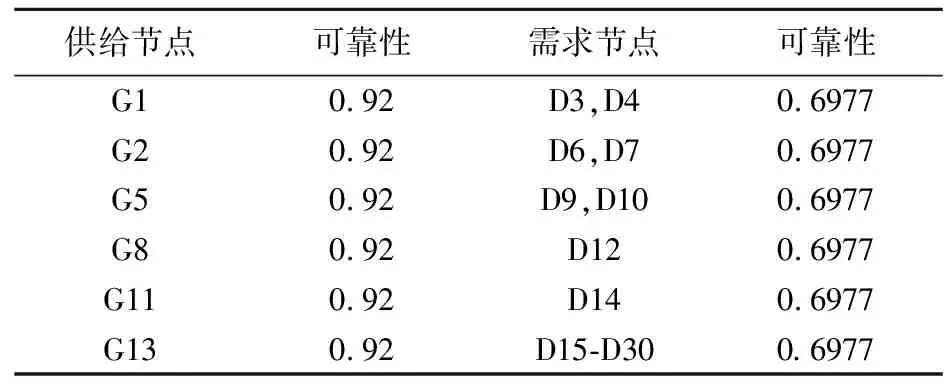
表1 供给节点与需求节点可靠性

根据风力发电网络图,供给节点与需求节点可靠性,得到风力发电系统可靠性R。Birnbaum重要度和综合重要度评估节点对风力发电系统可靠性的影响程度。根据公式(8)和公式(9),供给节点在Birnbaum重要度和综合重要度评估下对风力发电系统的影响如图4和图5所示。

图4 供给节点的Birnbaum重要度

根据Birnbaum重要度,供给节点可靠性对风力发电系统可靠性影响的优先级排序为节点G8、节点G13、节点G1、节点G11、节点G2、节点G5。其中,节点G8对风力发电系统可靠性的影响最大,节点G8的状态改变使系统可靠性变化最大。根据综合重要度,供给节点可靠性对风力发电系统性能影响的优先级排序为节点G8、节点G13、节点G11、节点G1、节点G2、节点G5。其中,节点G8对风力发电系统可靠性的影响最大,节点G8的状态改变使系统可靠性变化最大。

图5 供给节点的综合重要度

风力发电机是风力发电系统的核心,风力发电系统运行环境恶劣导致风力发电机故障,对经济造成严重损失。因此,在固定资源下对故障风力发电机进行可靠性排序维修是至关重要的。维修总成本为7万元。供给节点维修成本如表2所示。

表2 供给节点维修成本

在维修总成本约束下,可能的维修节点组合如表3所示。

表3 维修节点组合

故障节点组合PG1在Birnbaum重要度和综合重要度评估下的最优恢复顺序分别为G1,G11,G2和G11,G1,G2,风力发电系统可靠性提升分别为0.0386和0.0122;故障节点组合PG2在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G1,G5,风力发电系统可靠性提升分别为0.0260和0.0062;故障节点组合PG3在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G1,风力发电系统可靠性提升分别为0.0516和0.0133;故障节点组合PG4在Birnbaum重要度和综合重要度评估下的最优恢复顺序分别为G13,G1,G11和G13,G11,G1,风力发电系统可靠性提升分别为0.0507和0.0173;故障节点组合PG5在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G2,G5,风力发电系统可靠性提升分别为0.0472和0.0135;故障节点组合PG6在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G13,G11,G2,G5,风力发电系统可靠性提升分别为0.0463和0.0175;故障节点组合PG7在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G11,G2,风力发电系统可靠性提升分别为0.0526和0.0171;故障节点组合PG8在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G13,G2,风力发电系统可靠性提升分别为0.0593和0.0190;故障节点组合PG9在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G11,G5,风力发电系统可靠性提升分别为0.0526和0.0167;故障节点组合PG10在Birnbaum重要度和综合重要度评估下的最优恢复顺序均为G8,G13,G11,风力发电系统可靠性提升分别为0.0647和0.0222。因此,固定成本约束下使风力发电系统可靠性提升最大化的故障节点维修顺序为G8,G13,G11。

图6 风力发电系统的Birnbaum重要度梯度

曲面S是风力发电系统可靠性的等价曲面R=f(R1,R3,R8)=0.9502。向量R是梯度向量R是曲面S的法线,两者交点为A。风力发电系统在点A处的Birnbaum重要度为向量R的方向即为风力发电系统可靠性增长最快的方向。因此,管理者应使节点G1、节点G3和节点G8的可靠性向点A靠拢,确保系统可靠性沿最快方向增长。