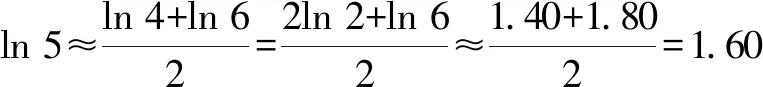幂指对大小比较四妙招
2023-02-11邱红英吴海军
邱红英 吴海军
江苏省镇江市丹徒高级中学
1 妙招一:引入媒介,巧取中间值
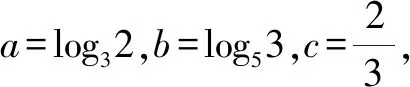
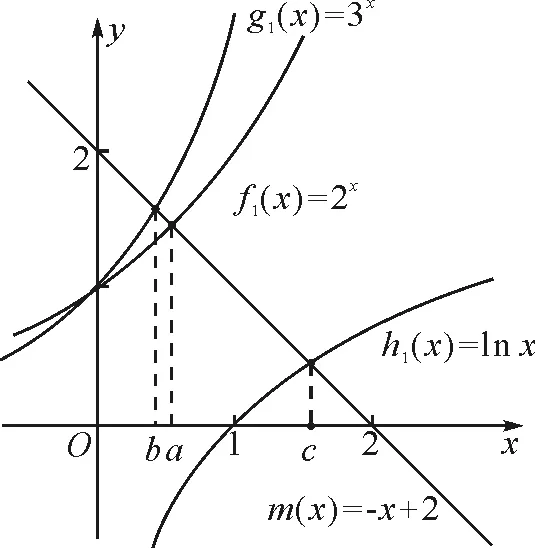
A.a C.b 故选:A. A.a C.c 解析:设f(x)=ln(1+x)-x(x>-1). 当x∈(-1,0)时,f′(x)>0; 当x∈(0,+∞)时,f′(x)<0. 所以,函数f(x)=ln(1+x)-x在(-1,0)上单调递增,在(0,+∞)上单调递减. 设g(x)=xex+ln(1-x)(0 令h(x)=ex(x2-1)+1,0 所以g(0.1)>g(0)=0,即0.1e0.1>-ln 0.9. 所以a>c. 故选:C. A.a C.b 解析:由a=2ln 1.01=ln 1.0201,b=ln 1.02,可得a>b. 于是g(t)=2ln(t2+3)-t+1-2ln 4,则 g(t)>g(1)=2ln 4-1+1-2ln 4=0. 故f(x)>0,可得a>c. 故选:B. 方法提炼:本组题目难度较大,关键在于将各个值中的共同的量用变量替换,构造函数,利用导数研究相应函数的单调性,进而比较大小.这样的问题,凭借近似估值计算往往是无法解决的. 例4a,b,c依次表示函数f(x)=2x+x-2,g(x)=3x+x-2,h(x)=lnx+x-2的零点,则a,b,c的大小顺序为( ). A.c C.a 解法2:几何法.因为a,b,c分别是函数f(x)=2x+x-2,g(x)=3x+x-2,h(x)=lnx+x-2的零点.所以a,b,c分别是函数f1(x)=2x,g1(x)=3x,h1(x)=lnx与m(x)=-x+2图象交点的横坐标.由图1可得b 图1 方法提炼:指数、对数型超越函数零点大小的比较,利用转化与化归、函数与方程、数形结合思想,将零点问题转化为函数图象的交点问题,通过作图进行大小比较.这种几何法的解题速度比较快. 例5已知a=log0.20.02,b=log660,c=ln 6,则下列选项正确的是( ). A.b C.c 解法1:由a=log0.20.02=1-log0.210=1+log510,b=log660=1+log610>1+log66=2,及log510>log610,得a>b>2.又c=ln 6 解法2::代值近似计算. 方法提炼:我们在题目中常见含有ln 2,ln 3,ln 5等值的大小比较问题,有时还是单选压轴题,如果能记住常见的这些对数值,就可以独辟蹊径,很快得出结论. 常用必备对数值有: ln 2≈0.70,ln 3≈1.10,ln π≈1.14,ln 5≈1.60,ln 6≈1.80,ln 7≈1.95. 由以上各例可知,指、对、幂大小比较的常用方法有: (1)底数相同,指数不同时,如ax1和ax2,利用指数函数y=ax的单调性比较大小. (3)底数相同,真数不同时,如logax1和logax2,利用对数函数y=logax的单调性比较大小. (4)底数、指数、真数都不同时,寻找中间变量0,1或者其他能判断大小关系的中间量,借助中间量进行大小关系的判定. (5)转化为两函数图象交点的横坐标. (6)估算法. 常用对数值有: ln 2≈0.70; ln 3≈1.10; ln π≈1.14; ln 6=ln 2+ln 3≈1.80; 希望大家在实际应用时灵活应变,选择最佳途径以达到事半功倍的效果.Z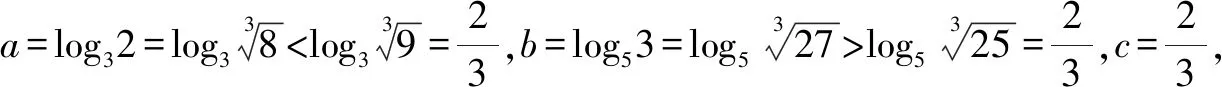
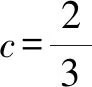
2 妙招二: 构造函数,单调性比大小
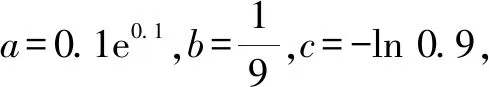
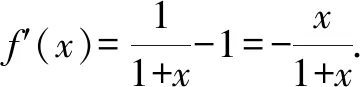
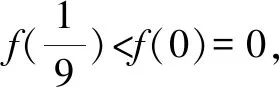
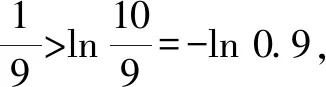
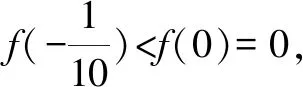
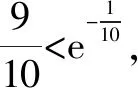
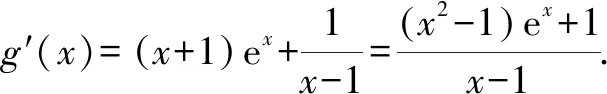
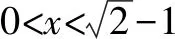
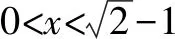
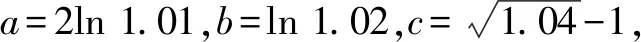
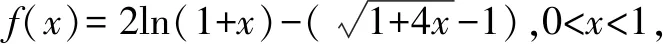


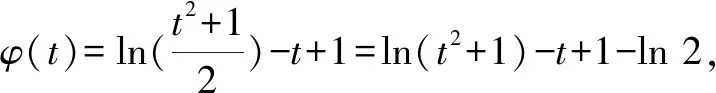
3 妙招三:数形结合,交点定大小
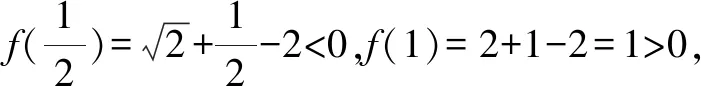
4 妙招四:应考绝招,代值求大小

5 方法总结