基于CPFS结构理论的“两角差的余弦公式”教学设计

王跃男 陈建强

哈尔滨师范大学教师教育学院

1 理论基础

1.1 CPFS结构理论

2002年南京师范大学喻平教授在综合分析认知心理学家对知识表征的一般研究基础上，引入了概念域、概念系、命题域、命题系四个概念，并将其复合结构称为CPFS结构.

一个数学概念C的所有等价定义的图式，叫做概念C的概念域.由数学概念与概念之间存在的特定的数学关系在个体头脑中形成的概念网络就是概念系.与一个命题等价的命题集的图式叫做这个命题的命题域.在一个命题集中，任意一个命题都至少与其他某一个命题有“推出”关系，就称这个命题集的图式为一个命题系.

CPFS结构揭示了概念、命题之间的联系，形成良好的CPFS结构有助于加强学生对知识的理解、知识迁移、数学能力的发展等.

1.2 CPFS结构理论下的两角差的余弦公式

三角函数是高中数学内容的重要组成部分，且与许多知识都有着密切的关联.由于三角函数命题系中大部分命题的推导都源于两角差的余弦公式，因此建立良好的两角差的余弦公式CPFS结构对学生形成三角恒等变换命题系有很大影响[1].

图1 三角函数模块的知识结构图

本研究将基于CPFS结构理论进行“两角差的余弦公式”的教学设计，帮助学生建立三角恒等变换公式的知识生长点，进而构建良好的三角函数知识结构(如图1所示).

2 教学设计

2.1 教材分析

两角差的余弦公式是学生在学习诱导公式与掌握单位圆工具的基础上，利用数形结合、特殊与一般等思想方法获得的.如图2，三角恒等变换与诱导公式具有广义抽象关系，对差角余弦公式进行强抽象可获得部分诱导公式，掌握差角的余弦公式可以为后续三角恒等变换公式作铺垫，因此两角差的余弦公式在教材中起着承上启下的重要作用[2].

图2 三角恒等变换命题域、命题系

2.2 教学目标

(1)经历两角差的余弦公式的证明过程，知道两角差的余弦公式的意义；能运用两角差的余弦公式解决简单的恒等变换问题.

(2)单位圆是研究三角函数的重要工具，借助它的直观更好地感悟三角函数的概念与性质，培养直观想象素养.

(3)通过对公式的具体推导与证明，培养数学运算素养和逻辑推理素养.

2.3 教学重难点

教学重点：推导两角差的余弦公式；利用两角差的余弦公式解决一些三角恒等变换问题.

教学难点：差角余弦公式的推导.

2.4 教学过程

2.4.1 设置情景，导入新课

问题1三角函数这一章我们学过很多重点内容，一起来复习几个诱导公式：

①sin(π+α)=________;②cos(π-α)= ______;

学生：①-sinα； ②-cosα； ③cosα； ④sinα.

追问1：它们在形式上有哪些共同点呢？等号左侧与等号右侧分别是什么角的三角函数？

学生：等号左侧是轴上角与任意角的和或差的三角函数；等号右侧与任意角三角函数有关.

这节课先研究，对于任意角α,β，cos(α-β)=？

设计意图：复习部分诱导公式，强调诱导公式与三角恒等变换的广义抽象关系，为接下来建构三角恒等变换命题系作铺垫.通过所提问题引出研究对象，激发学生兴趣，明确研究和差角公式的必要性.

2.4.2 建立联系，感知命题

问题2猜想一下，cos(α-β)可能等于？

学生：cosα-cosβ.

追问1：它是否成立？请验证并说明你的结论.

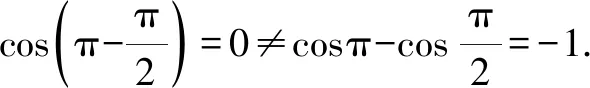
追问2：我们是否学过cos(α-β)的特殊情况？

问题3观察上述由强抽象得出的诱导公式，你认为cos(α-β)与这些诱导公式之间具有怎样的关系？cos(α-β)的展开结果可能与α，β哪些三角函数有关？

学生：特殊到一般的关系.cos(α-β)的展开结果可能与sinα，sinβ，cosα，cosβ有关.

设计意图：基于部分诱导公式与差角的余弦公式之间的抽象关系，引导学生得出cos(α-β)展开后出现的基本项.学生积累了从具体到抽象的活动经验，运用了特殊到一般的思想方法，锻炼了数学抽象素养.

2.4.3 深入探究，发现命题

问题4回顾一下cos(α-β)的特殊情况——诱导公式的得出，我们采取了什么方法？

学生：在单位圆中，利用圆的轴对称性和中心对称性得出等量关系，代入坐标.

问题5既然cos(α-β)是更一般的诱导公式，这节课我们继续利用这个思路.首先，请大家在练习纸中作出单位圆、任意角与终边.

学生作图时，教师巡视并选择几种角的终边处于不同象限的图形(如图3～6)，进行投影展示，选择一种(如图3)画在黑板上.

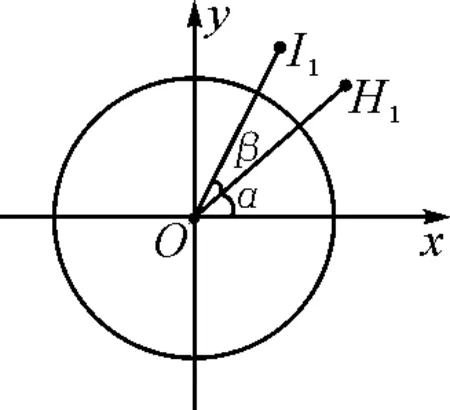
图3

图4

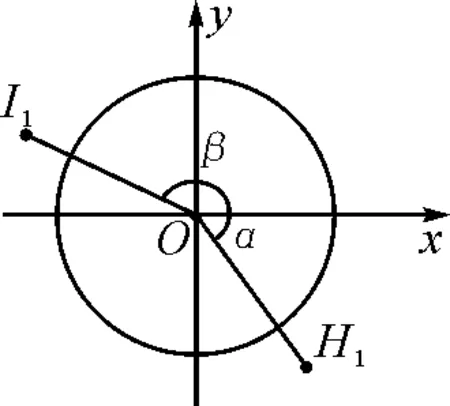
图5

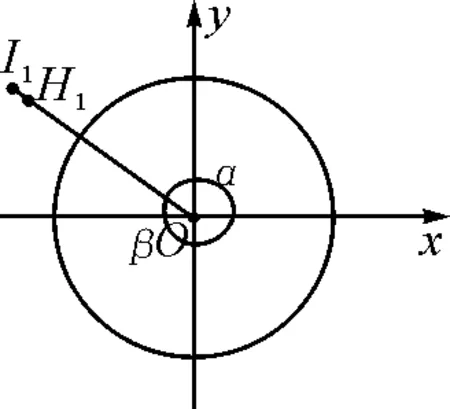
图6

问题6请同学们观察，任意角α与β终边的关系能怎样分类？

学生：终边可分为重合或不重合.

追问：那怎样用数学语言描述呢？

学生：终边不重合时，α≠2kπ+β(k∈Z)；终边重合时,α=2kπ+β(k∈Z).

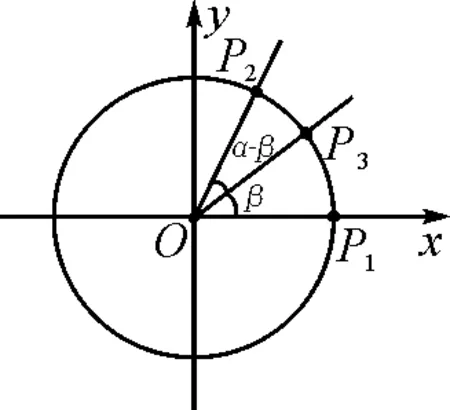
图7

问题7如图7，先选取第一种情况进行验证，设x轴非负半轴、α的终边、β的终边与单位圆交点依次记为P1，P2，P3，你能写出它们的坐标吗？

学生：P1(1，0)，P2(cosα，sinα)，P3(cosβ，sinβ).

问题8观察交点的横纵坐标，要想获得公式,图中缺少了哪个重要的量？

学生：cos(α-β).

追问1：如何能出现cos(α-β)？

学生：由三角函数定义，角α-β始边在x轴非负半轴时，终边与单位圆交点横坐标为cos(α-β).

追问2：如何让角α-β的始边落在x轴非负半轴，同时角的大小保持不变[3]?

学生：旋转.

打开准备好的几何画板，展示角α-β的旋转过程，记旋转后的α-β终边与单位圆交于点P4(如图8).

设计意图：引导学生在单位圆中构造出公式中的所需内容，为应用圆的旋转对称性作铺垫.

图8

问题9如图8,显然P4坐标为(cos(α-β)，sin(α-β))，至此我们终于将所需三角函数值全部找到.回想获得诱导公式的过程，建立单位圆后，利用圆的轴对称和中心对称性寻找等量关系.对于更为一般的cos(α-β)公式，我们可以利用圆更为一般的对称性是什么？

学生：圆的旋转对称性.

追问：根据圆的旋转对称性，你能发现哪些等量关系？

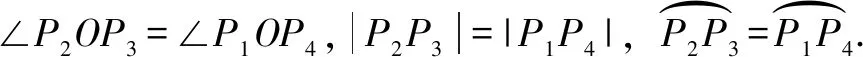
问题10：哪种等量关系便于代入坐标计算？怎样计算？

学生：|P2P3|=|P1P4|，利用两点间距离公式.

设计意图：利用单位圆的几何直观形成数与形的联系，通过几何画板展示数学问题的直观模型，渗透了数形结合思想，启发学生获得公式的方法，发展了学生的直观想象素养.

问题11利用等量关系|P2P3|=|P1P4|，结合两点间距离公式，你能否完成公式的证明？

学生计算过程中，教师巡视，将学生写的证明过程利用投影展示出来.

问题12至此我们的公式是否完整？不完整的话，缺少什么？

学生：不完整，缺少对α=2kπ+β，k∈Z情况的证明.

追问：那请大家继续完成公式的证明.

验证后发现：对于任意角α，β，有cos(α-β)=cosαcosβ+sinαsinβ.称为差角的余弦公式，简记为C(α-β).

设计意图：在教师的引导下，学生以已获得的相关的诱导公式为逻辑依据，将差角的余弦公式纳入认知结构，形成新的三角恒等变换命题系.在命题获得过程中，让学生积累运算经验，发展学生运算能力，养成一丝不苟、严谨求实的科学精神.

2.4.4 命题应用，巩固练习

练习1利用公式C(α-β)证明：

(2)cos(π-α)=-cosα.

设计意图：层层递进训练，加深学生对公式的理解和应用.应用新获得的差角的余弦公式命题，使学生逐步形成稳固的命题域和命题系.

2.4.5 课堂小结，回味公式

结合学习过程，举例说明你学习了哪些知识，收获哪些思想方法？说说印象最深的是什么？

设计意图：由学生总结本节课收获，加强学生对所学知识的印象，巩固新获得的命题域，建立诱导公式与三角恒等变换的命题系，培养总结反思习惯.

3 总结

数学命题的学习需要经历命题的获得、命题的证明、命题的应用三个心理阶段.这三个阶段可以使学生通过上下位学习、同位学习、并列学习，逐步形成稳固的命题域和命题系，改组、丰富和完善个体的认知结构，这也是数学命题学习的高级目标和本质.让学生明晰差角的余弦公式与诱导公式的抽象关系，并经过等价变式获得两角和的余弦公式，可以使学生形成良好的三角函数命题系，帮助学生减轻学习负担，提高数学知识应用能力.